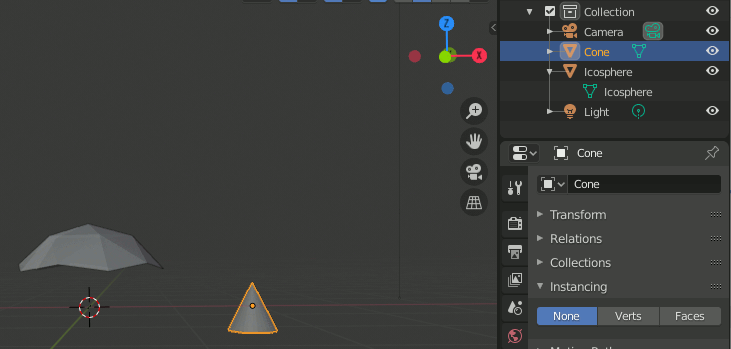
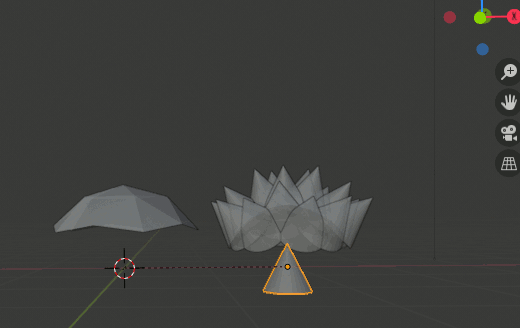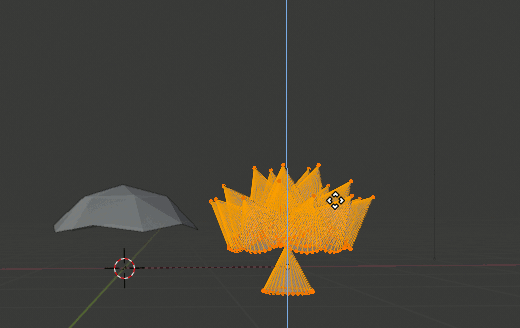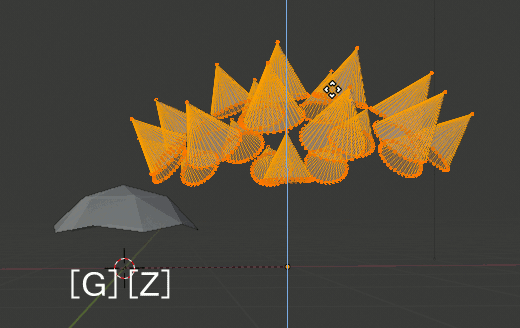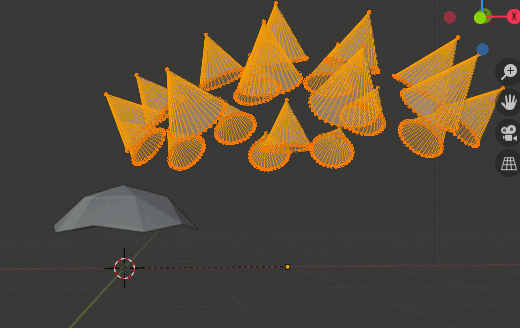
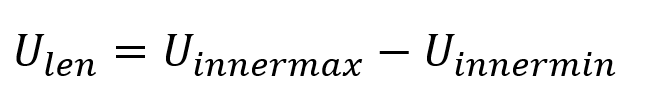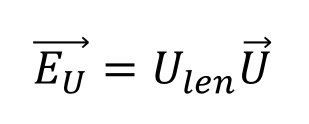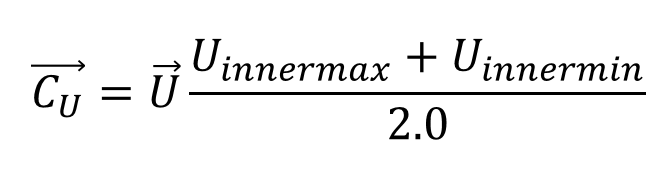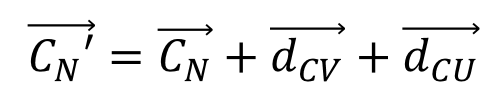Blender 2.8 instancing機能について
instancing機能はオブジェクトを複製する機能と言える。検索するとParticle Hairのように見える例が散見されるが、どちらかというとArrayモディファイアに近いと思う。
というかなんでモディファイアではないんだ。
instancingの考え方
① 「複製したいオブジェクト」と「複製の基準となるオブジェクト」を用意
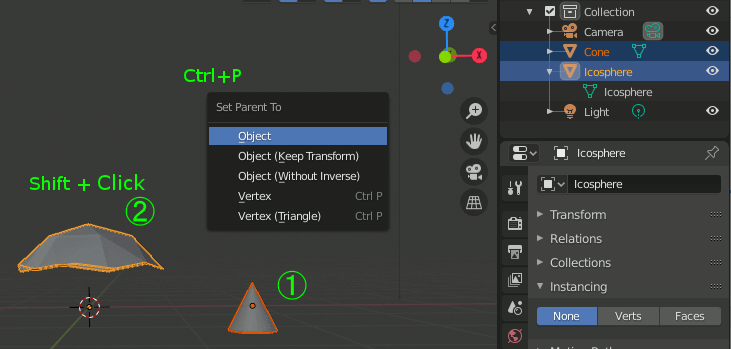
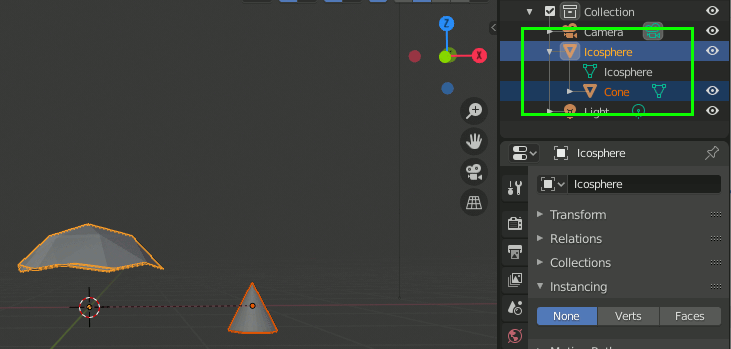
② 基準(親) - 複製したいオブジェクト(子)の関係を作る
③ 複製方法(面基準か頂点基準か)を選択する
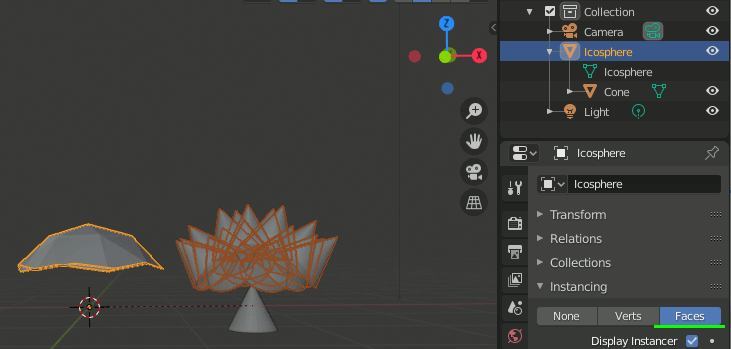
実体化
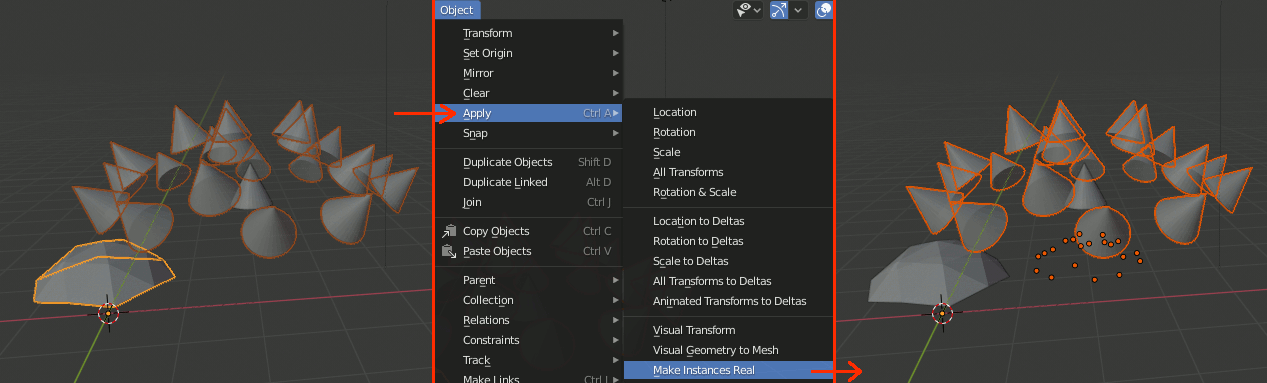
基準としたオブジェクトを選択し、[Object]→[Apply]→[Make Instances Real]で複製したオブジェクトを実体化する
二次元のN角形の頂点座標の計算
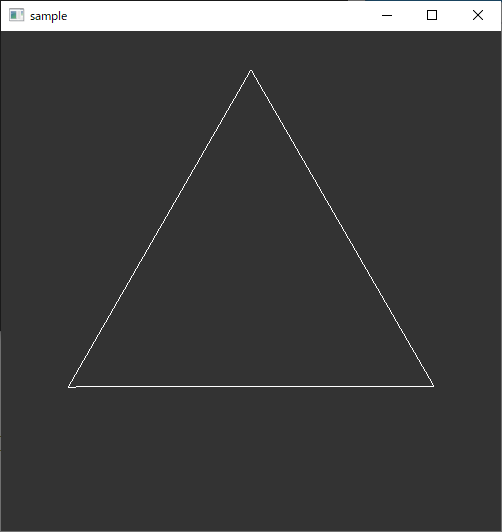
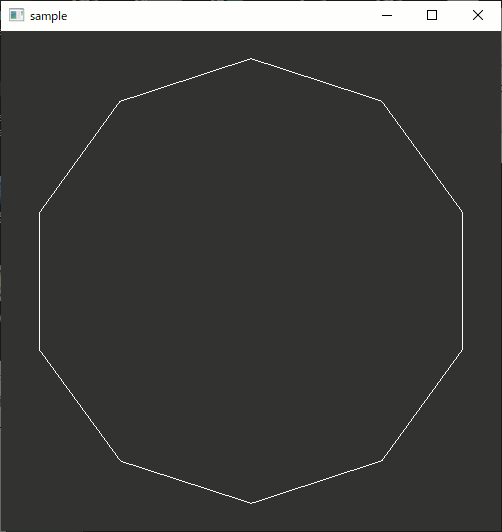
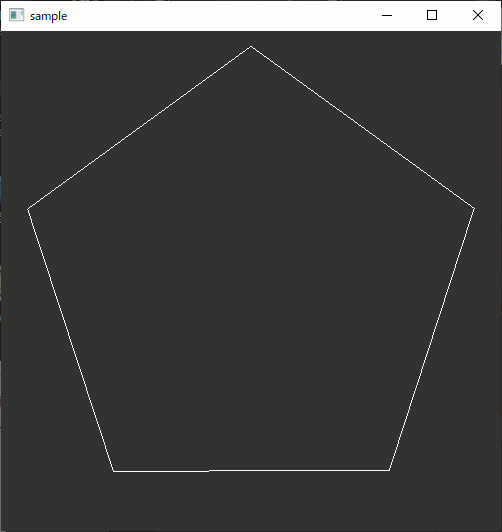
たまに欲しくなる、三角形とか五角形とかの座標計算をする。
実のところ円を描くのと全く同じ。以前円を描くプログラムを書いた。
これを書いた当時は事情によりこの方法の法が簡単だったのだけれどやはり普通の方法の方が簡単だ。
コード
//! @tparam Point2D 二次元座標を一つ表現する。operator[](int)が必要 //! @brief 多角形を作成する //! @param [out] points 作成した多角形の頂点 //! @param [in] N 頂点数 //! @param [in] radius 中心から頂点までの距離 //! @return なし template<typename Point2D> void createNgon( std::vector< Point2D >& points, const int N, const double radius = 1.0 ) { for (size_t i = 0; i < N; i++) { double t = 2 * 3.14 / N * i; double x = sin(t); double y = cos(t); Point2D p; p[0] = x * radius; p[1] = y * radius; points.push_back(p); } }
使用例
//多角形作成 std::vector<std::array<double, 2>> ngon; createNgon(ngon,3); //表示 glPointSize(1); glBegin(GL_LINE_LOOP); for (size_t i = 0; i < ngon.size(); i++) { glVertex2dv(ngon[i].data()); } glEnd();
Blender 2.8 Create Grass Fast Blender Tutorial 抜粋
これも無駄の多いチュートリアルなので抜粋する
草一本を作成
[Shift+A]→[Mesh]→[Plane]でPlaneを一つ追加し、Proportional Editingを使って草一本分をモデリングする
※ なおマテリアルを設定するならこの時が一番いい。
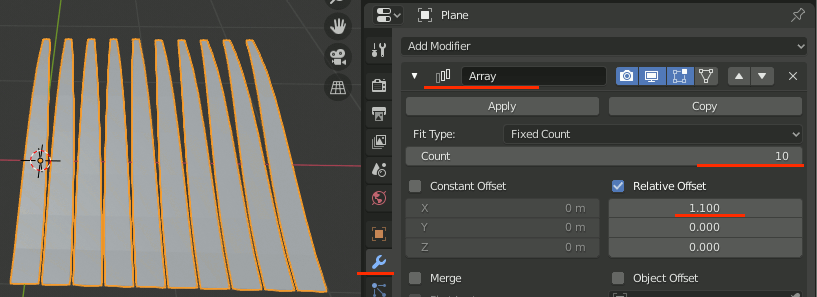
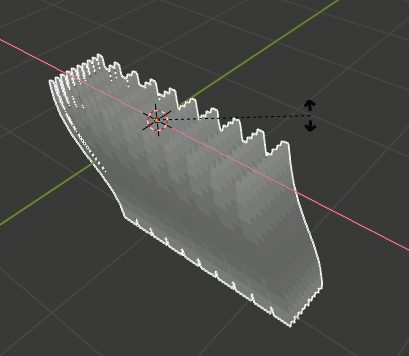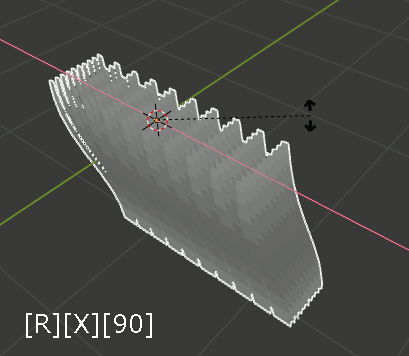
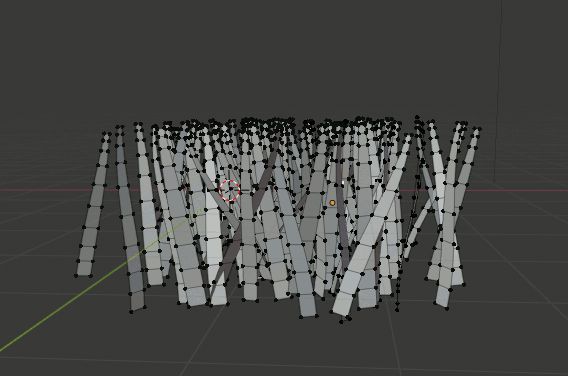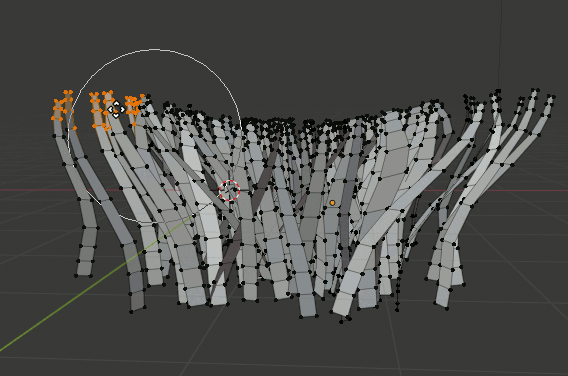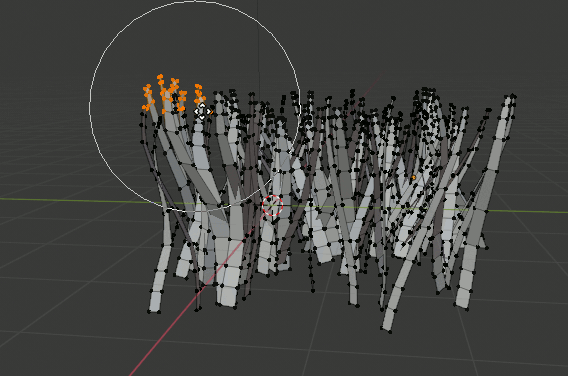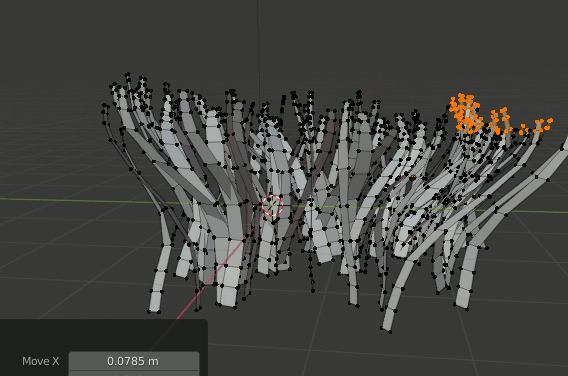
一本をコピーして100本(10x10)作成
草一本にArrayモディファイアを追加し、僅かに間隔を開けて10個複製する。
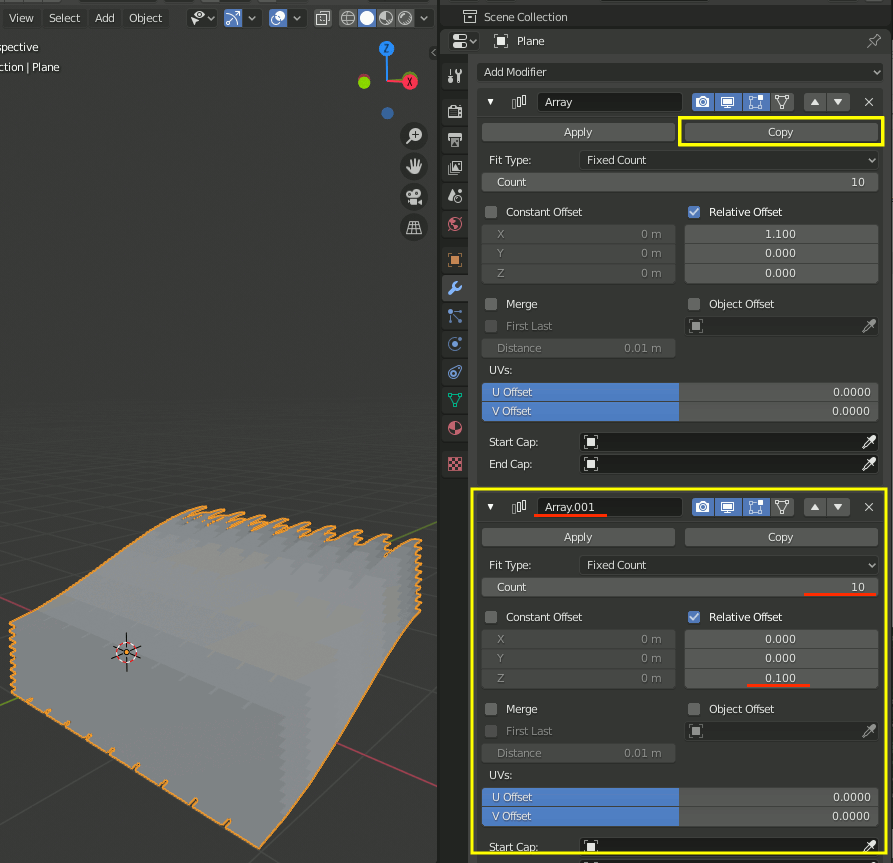
さらに、ArrayモディファイアをCopyしArray.001を作成、Relative OffsetをXを0、Zを0.1に設定する。
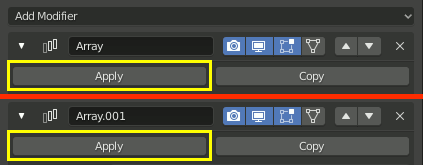
両方のArrayモディファイアをApplyする。
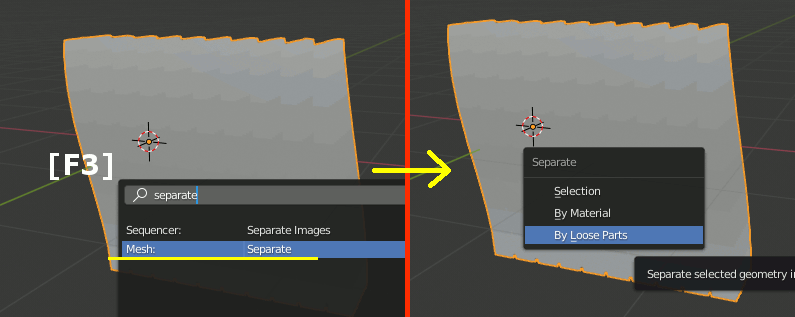
F3キーを押し、separateを検索、 By Loose Partsで非連続な部分を全て別オブジェクトに変換する
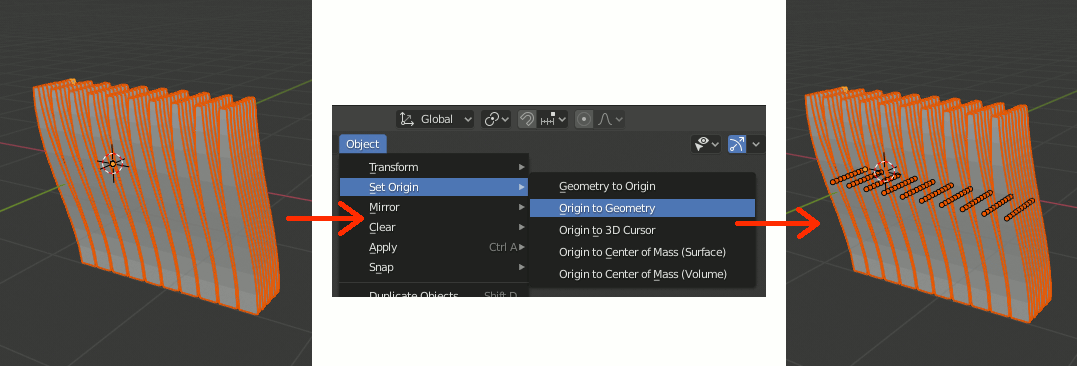
なお分割後、Origin to GeometryでOriginを各モデルの重心に移動しておく。
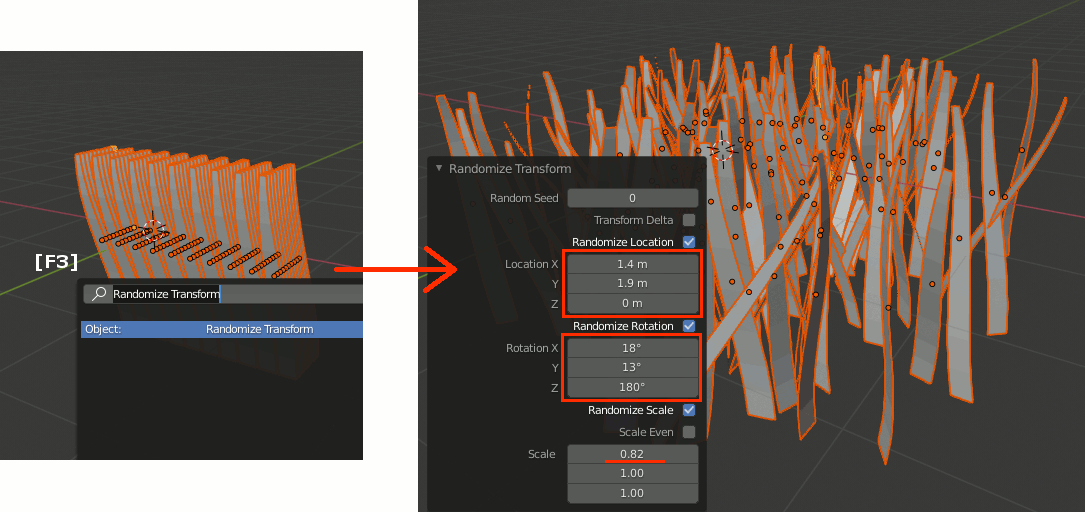
ランダムに再配置・結合
F3でRandomize Transformを検索し、Location、Rotation、Scaleを適当に設定する。この時、Rotation Zは180度回転させるが、その他は余り極端にしない。Locationを大きくしすぎると散らばりすぎる。
Randomize Transformが終わったら全部選択されている状態でCtrl+Jを押し、一つのオブジェクトにまとめる
形を整える
Proportional Editingを使って草っぽい広がり方にする
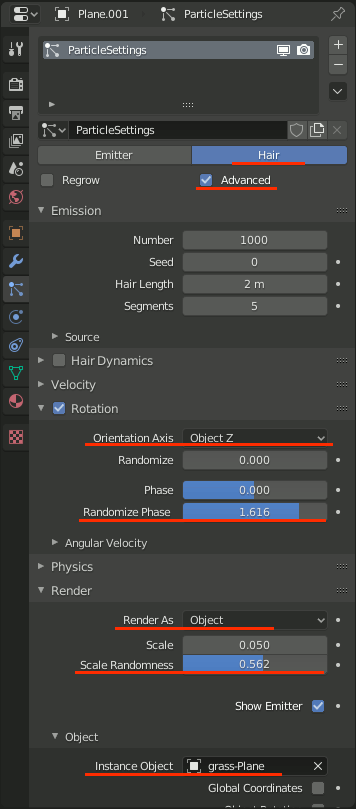
Particle hairで配置
平面を追加し、Particleを追加→Hairを選択。Advancedにチェックを入れる。
Hairにオブジェクトを設定:
・Render → Render As = Object
・Render → Object → Instance Object = 草のオブジェクト
草のランダム回転:
・Rotation → Orientation Axis = ObjectZ
・Rotation → Randomize Phase = 任意
草のランダムサイズ変更:
・Render → Scale Randomness
同じ原理でテクスチャを設定した場合
OBBを計算する(プログラム)
プログラム本体
#pragma once #include <vector> #include <array> #include <limits> #include <valarray>
template<typename real_t> real_t Length3(const real_t * const vec) { const int X = 0; const int Y = 1; const int Z = 2; return sqrt(vec[X] * vec[X] + vec[Y] * vec[Y] + vec[Z] * vec[Z]); } template<typename real_t> bool Normalize3(real_t* const pV) { const int X = 0; const int Y = 1; const int Z = 2; real_t len; real_t& x = pV[X]; real_t& y = pV[Y]; real_t& z = pV[Z]; len = static_cast<real_t>(sqrt(x * x + y * y + z * z)); if (len < static_cast<real_t>(1e-6)) return false; len = static_cast<real_t>(1.0) / len; x *= len; y *= len; z *= len; return true; } template<typename real_t> real_t Inner3(real_t const* const vec1, real_t const* const vec2) { const int X = 0; const int Y = 1; const int Z = 2; return ((vec1[X]) * (vec2[X]) + (vec1[Y]) * (vec2[Y]) + (vec1[Z]) * (vec2[Z])); }
/*! * Jacobi法による固有値の算出 * @param[inout] a 実対称行列.計算後,対角要素に固有値が入る * @param[out] v 固有ベクトル(aと同じサイズ) * @param[in] n 行列のサイズ(n×n) * @param[in] eps 収束誤差 * @param[in] iter_max 最大反復回数 * @return 反復回数 * @see http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%B8%C7%CD%AD%C3%CD/%B8%C7%CD%AD%A5%D9%A5%AF%A5%C8%A5%EB */ template<typename real_t> int EigenJacobiMethod(real_t* a, real_t* v, int n, real_t eps = 1e-8, int iter_max = 100) { real_t bii, bij, bjj, bji; auto bim = std::vector<real_t>(n); auto bjm = std::vector<real_t>(n); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { v[i * n + j] = (i == j) ? 1.0 : 0.0; } } int cnt = 0; for (;;) { int i, j; float x = 0.0; for (int ia = 0; ia < n; ++ia) { for (int ja = 0; ja < n; ++ja) { int idx = ia * n + ja; if (ia != ja && fabs(a[idx]) > x) { i = ia; j = ja; x = std::abs(a[idx]); } } } float aii = a[i * n + i]; float ajj = a[j * n + j]; float aij = a[i * n + j]; float alpha, beta; alpha = (aii - ajj) / 2.0; beta = sqrt(alpha * alpha + aij * aij); float st, ct; ct = sqrt((1.0 + fabs(alpha) / beta) / 2.0); // sinθ st = (((aii - ajj) >= 0.0) ? 1.0 : -1.0) * aij / (2.0 * beta * ct); // cosθ // A = PAPの計算 for (int m = 0; m < n; ++m) { if (m == i || m == j) continue; float aim = a[i * n + m]; float ajm = a[j * n + m]; bim[m] = aim * ct + ajm * st; bjm[m] = -aim * st + ajm * ct; } bii = aii * ct * ct + 2.0 * aij * ct * st + ajj * st * st; bij = 0.0; bjj = aii * st * st - 2.0 * aij * ct * st + ajj * ct * ct; bji = 0.0; for (int m = 0; m < n; ++m) { a[i * n + m] = a[m * n + i] = bim[m]; a[j * n + m] = a[m * n + j] = bjm[m]; } a[i * n + i] = bii; a[i * n + j] = bij; a[j * n + j] = bjj; a[j * n + i] = bji; // V = PVの計算 for (int m = 0; m < n; ++m) { float vmi = v[m * n + i]; float vmj = v[m * n + j]; bim[m] = vmi * ct + vmj * st; bjm[m] = -vmi * st + vmj * ct; } for (int m = 0; m < n; ++m) { v[m * n + i] = bim[m]; v[m * n + j] = bjm[m]; } float e = 0.0; for (int ja = 0; ja < n; ++ja) { for (int ia = 0; ia < n; ++ia) { if (ia != ja) { e += fabs(a[ja * n + ia]); } } } if (e < eps) break; cnt++; if (cnt > iter_max) break; } return cnt; } //! @brief 固有値・固有ベクトル struct _eigen_ { double _value; //!< 固有値 double _vector[3];//!< 固有ベクトル }; //! @brief データの平均を求める //! @param [in] vec データの配列 //! @return 各要素の平均 template<typename real_t,typename PointT> void Covariance_Ave(real_t* ave,const std::vector<PointT>& vec) { // 初期化 ave[0] = 0; ave[1] = 0; ave[2] = 0; // 各要素平均 for (size_t i = 0; i < vec.size(); i++) { ave[0] += vec[i][0]; ave[1] += vec[i][1]; ave[2] += vec[i][2]; } ave[0] /= vec.size(); ave[1] /= vec.size(); ave[2] /= vec.size(); } //! @brief 共分散を求める //! @param [in] average 各要素の平均 3次元 //! @param [in] vec データ //! @param [in] param どの要素に対して求めるか。例えばxyzの時、x,yに対する共分散なら{0,1}を与える。 //! @return 偏差の積の和の要素数分の一 template<typename real_t,typename PointT> double Covariance(const real_t* const average, const std::vector<PointT>& vec, const std::array<int, 2>& param) { double sum = 0.0; for (size_t i = 0; i < vec.size(); i++) { //指定したパラメータの偏差を求める double deviation[3]; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; deviation[target] = (vec[i][target] - average[target]); } //偏差の積 double product = 1.0; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; product *= deviation[target]; } //偏差の積の和を更新 sum += product; } //偏差の積の和のN分の一 return 1.0 / vec.size() * sum; } //! @brief データを主成分分析する //! @param [out] average 全データの各要素の平均 //! @param [out] ev 固有値と固有ベクトル //! @param [in] pt 三次元の座標値一覧 //! @return なし template<typename PointT> void PrincipalComponentAnalysis3D(_eigen_* e, const std::vector<PointT>& pt) { double average[3]; //各要素の平均を求める。 //これは共分散を求めるときに (x[i] - xの平均)×(y[i] - yの平均) 等の計算が必要なため Covariance_Ave(average, pt); //共分散を求める //第三引数の{0,0}はxxを表す。xyなら{0,1}。これはデータがxyzの順に並んでいる事が前提。 double Sxx = static_cast<double>(Covariance(average, pt, { 0, 0 })); double Sxy = static_cast<double>(Covariance(average, pt, { 0, 1 })); double Sxz = static_cast<double>(Covariance(average, pt, { 0, 2 })); double Syy = static_cast<double>(Covariance(average, pt, { 1, 1 })); double Syz = static_cast<double>(Covariance(average, pt, { 1, 2 })); double Szz = static_cast<double>(Covariance(average, pt, { 2, 2 })); // 分散共分散行列 double a[3 * 3] = { Sxx,Sxy,Sxz, Sxy,Syy,Syz, Sxz,Syz,Szz }; double eigen[3 * 3]; EigenJacobiMethod(a, eigen, 3); // eigenの対角線が固有値となっている e[0]._value = eigen[0]; e[0]._vector[0] = eigen[0]; e[0]._vector[1] = eigen[3]; e[0]._vector[2] = eigen[6]; e[1]._value = eigen[4]; e[1]._vector[0] = eigen[1]; e[1]._vector[1] = eigen[4]; e[1]._vector[2] = eigen[7]; e[2]._value = eigen[8]; e[2]._vector[0] = eigen[2]; e[2]._vector[1] = eigen[5]; e[2]._vector[2] = eigen[8]; }
// OBBを表現する構造体
struct OBBObject { double corner[3]; //OBBの角 double vectorU[3]; //各辺の方向と長さ double vectorV[3]; double vectorN[3]; };
inline std::valarray<double> shift_centersUV( const std::valarray<double>& centerU, const std::valarray<double>& centerV, const std::valarray<double>& centerN, const std::valarray<double>& vectorU, const std::valarray<double>& vectorV, const std::valarray<double>& vectorN ) { ////////////////////////////////////////// // vector vectorU→centerV std::valarray<double> vRG = centerV - centerU; double Rlen = Inner3(&vectorU[0], &vRG[0]); Rlen /= Length3(&vectorU[0]); std::valarray<double> direction_uv = vectorU; Normalize3(&direction_uv[0]); direction_uv *= -Rlen; glLineWidth(2); glColor3d(1, 0, 0); ////////////////////////////////////////// // vector centerV→centerU std::valarray<double> vGR = centerU - centerV; double Glen = Inner3(¢erV[0], &vGR[0]); Glen /= Length3(¢erV[0]); std::valarray<double> direction_vc = centerV; Normalize3(&direction_vc[0]); direction_vc *= -Glen; ////////////////////////////////////////// return direction_uv + direction_vc; } inline std::valarray<double> get_a_corner( const std::valarray<double>& centerU, const std::valarray<double>& centerV, const std::valarray<double>& centerN, const std::valarray<double>& vectorU, const std::valarray<double>& vectorV, const std::valarray<double>& vectorN ) { std::valarray<double> ret; ///////////////////////////// // OBBの中央を見つける ///////////////////////////// std::valarray<double> trueCenter = centerN + shift_centersUV( centerU, centerV, centerN, vectorU, vectorV, vectorN ); /////////////////////////////////////// // OBBの中央から各辺の半分ずつ移動する /////////////////////////////////////// ret = trueCenter - (vectorU/2.0) - (vectorV/2.0) - (vectorN/2.0); return ret; } //! @brief 点群を囲むOBBを求める //! @param [in] obb BoundingBoxを表現する構造体 //! @param [in] pt 計算対象の頂点 template<typename PointT> void CalcOBB(OBBObject* obb, const std::vector<PointT> pt) { using scalar_t = double; _eigen_ e[3]; PrincipalComponentAnalysis3D(e, pt); //降順ソート std::sort(std::begin(e), std::end(e), [](const _eigen_ & e1, const _eigen_ & e2) { return e1._value > e2._value; }); scalar_t obbLen[3];//ボックス辺長さ std::array<std::valarray<double>, 3> centerd; centerd[0] = std::valarray<double>(3); centerd[1] = std::valarray<double>(3); centerd[2] = std::valarray<double>(3); for (int k = 0; k < 3; k++) { scalar_t inner_k_min = (std::numeric_limits<scalar_t>::max)(); scalar_t inner_k_max = std::numeric_limits<scalar_t>::lowest(); //第 k+1 主成分とすべての頂点の内積のうち最大・最小を取り出す for (size_t i = 0; i < pt.size(); i++) { scalar_t p[3] = { pt[i][0], pt[i][1], pt[i][2] }; inner_k_min = (std::min)( Inner3(p, e[k]._vector), inner_k_min ); inner_k_max = (std::max)( Inner3(p, e[k]._vector), inner_k_max ); } obbLen[k] = (inner_k_max - inner_k_min); scalar_t tmp = (inner_k_max + inner_k_min) / 2.0; centerd[k][0] = e[k]._vector[0] * tmp; centerd[k][1] = e[k]._vector[1] * tmp; centerd[k][2] = e[k]._vector[2] * tmp; } /////////////////////////////// std::valarray<double> vecu = { e[0]._vector[0] * obbLen[0], e[0]._vector[1] * obbLen[0], e[0]._vector[2] * obbLen[0] }; std::valarray<double> vecv = { e[1]._vector[0] * obbLen[1], e[1]._vector[1] * obbLen[1], e[1]._vector[2] * obbLen[1] }; std::valarray<double> vecn = { e[2]._vector[0] * obbLen[2], e[2]._vector[1] * obbLen[2], e[2]._vector[2] * obbLen[2] }; std::valarray<double> ret = get_a_corner( centerd[0], centerd[1], centerd[2], vecu, vecv, vecn ); obb->corner[0] = ret[0]; obb->corner[1] = ret[1]; obb->corner[2] = ret[2]; obb->vectorU[0] = vecu[0]; obb->vectorU[1] = vecu[1]; obb->vectorU[2] = vecu[2]; obb->vectorV[0] = vecv[0]; obb->vectorV[1] = vecv[1]; obb->vectorV[2] = vecv[2]; obb->vectorN[0] = vecn[0]; obb->vectorN[1] = vecn[1]; obb->vectorN[2] = vecn[2]; }
呼び出し方
std::vector<std::vector<double> > points; //点群の読み込み先 read_xyz(points,"C:\\test\\Suzanne.xyz",' '); //点群読み込み CalcOBB(&obb, points);// OBB計算
なお以下はxyzファイル読み込み
//! @brief separator区切りの実数の一覧を読み込む //! @details xyzフォーマットは正式な規格として存在しないらしいので、ある程度の柔軟性を持たせる //! @param [out] ret 結果を格納する配列の配列 //! @param [in] filename ファイル名 //! @param [in] separator 区切り文字 //! @return なし template<typename scalar_t> void read_xyz(std::vector<std::vector<scalar_t> >& ret,const char* filename, const char separator) { std::ifstream ifs(filename); std::string str; while (std::getline(ifs, str)) { std::stringstream line{ str }; std::string value; std::vector<scalar_t> tmp; while (getline(line, value, separator)){ tmp.push_back(std::atof(value.c_str())); } ret.push_back(tmp); } }
OBB 表示関数
//! @brief 立方体を描画 //! @param [in] width 立方体の一辺の長さ //! @return なし void draw_obb(const OBBObject& obb) { double xs = obb.corner[0]; double ys = obb.corner[1]; double zs = obb.corner[2]; glEnable(GL_DEPTH_TEST); glFrontFace(GL_CCW);//時計回りが表 glEnable(GL_CULL_FACE);//カリングを有効にする glBegin(GL_LINE_LOOP); glColor3d(0.5, 0.5, 1.0); glVertex3d(xs, ys, zs);// glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2]); glVertex3d( xs + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2]); glEnd(); glBegin(GL_LINE_LOOP); glColor3d(0.0, 0.0, 1.0); glVertex3d( xs + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorU[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorN[2] + obb.vectorU[2]); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2]);// glEnd(); glBegin(GL_LINE_LOOP); glColor3d(1.0, 0.0, 0.0); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2] ); glVertex3d( xs + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorV[2] ); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2] ); glVertex3d(xs, ys, zs);// glEnd(); glBegin(GL_LINE_LOOP); glColor3d(1.0, 0.5, 0.5); glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2]);// glVertex3d( xs + obb.vectorU[0] + obb.vectorN[0], ys + obb.vectorU[1] + obb.vectorN[1], zs + obb.vectorU[2] + obb.vectorN[2] ); glVertex3d( xs + obb.vectorU[0] + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorN[2] + obb.vectorV[2] ); glVertex3d( xs + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorV[2] ); glEnd(); glLineWidth(2); glColor3d(0, 1, 0); glBegin(GL_LINE_LOOP); glVertex3d( xs, ys, zs); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2] ); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorN[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2] ); glEnd(); glColor3d(0.5, 1, 0.5); glBegin(GL_LINE_LOOP); glVertex3d( xs + obb.vectorV[0] + obb.vectorU[0], ys + obb.vectorV[1] + obb.vectorU[1], zs + obb.vectorV[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorV[0] + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorV[1] + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorV[2] + obb.vectorN[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorV[0] + obb.vectorN[0], ys + obb.vectorV[1] + obb.vectorN[1], zs + obb.vectorV[2] + obb.vectorN[2] ); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2]); glEnd(); glDisable(GL_CULL_FACE);//カリングを無効にする }

OBBを計算する(計算方法)
OBBとAABB
OBBは物体を最小で囲むBoundingBoxの事で、無駄なく囲めるが求めるのが難しい。
AABBは物体のX軸Y軸Z軸の最大-最小からなるBoundingBoxで、求めるのがきわめて簡単だが無駄が多い。
主成分分析
以前、主成分分析で点群の法線を求めた。三次元の点群に主成分分析をかけた結果出てきた第一、第二、第三主成分を使えばOBBが求められる。
参考文献
以下のサイトをなぞっていく。
http://www.nomuraz.com/denpa/prog005.htm
手順
① OBBの各辺の方向を求める
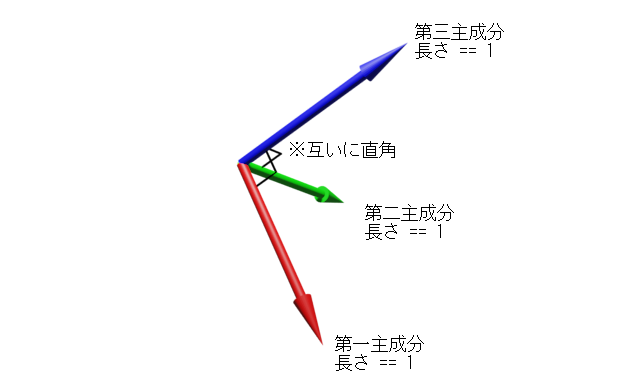
三次元点群データを主成分分析すると、固有ベクトルが三つ(第一、第二、第三主成分)得られる。
この三つのベクトルは互いに垂直で且つ長さが1になっている。
この各ベクトルが、OBBの各辺の方向となる。
つまり、各辺の方向は主成分分析の結果そのものである。
面の抽出の時は広がりの一番小さい方向を表す第三主成分を使ったがOBBの時は三つとも使うことになる。
以下、各ベクトルを→U , →V , →N とする。
② OBBの各辺の長さ
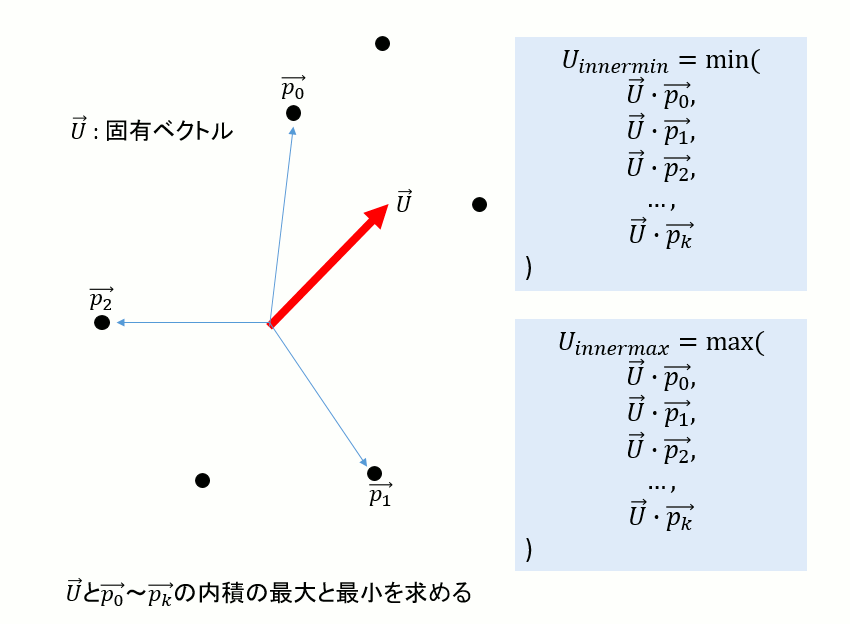
方向がわかったので次は辺の長さを求める。
まず、固有ベクトルについて、そのベクトルとすべての頂点座標(位置ベクトル)の内積をとり、その最大・最小を求める。
こうして求めたU,V,Nの(max-min)の値が、各方向の辺の長さとなる
この計算を、→U , →V , →N それぞれについて行う。
そして、OBBの辺としての長さがわかったので、各辺をベクトルで表すと、
これでエッジの長さと方向を表す→EU , →EV , →ENが求められた。
③ OBBの各辺の中央
各内積の最大と最小を足して2で割り、各ベクトルを掛けると、各辺の中央が求められる
この計算も、→U , →V , →N それぞれについて行う。
これを→CU , →CV , →CNとする。
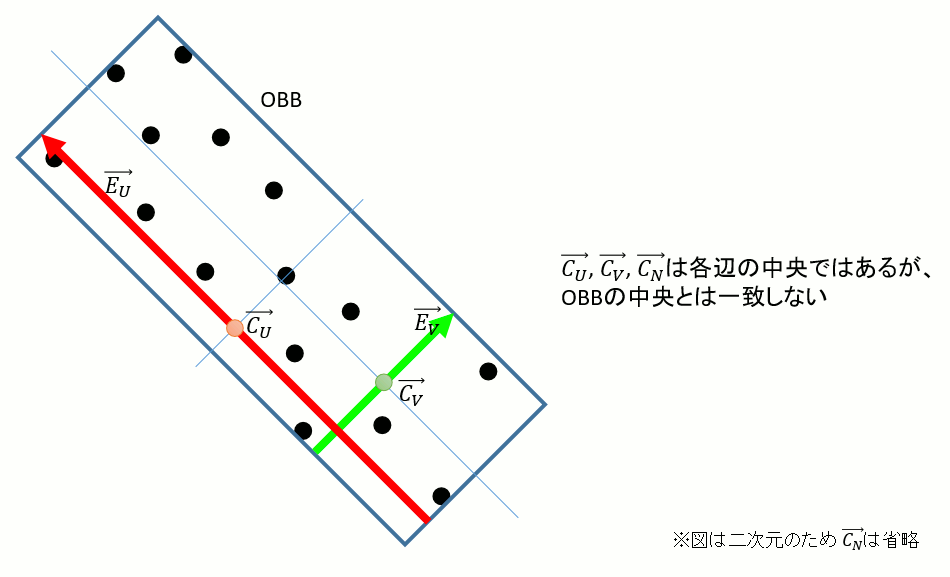
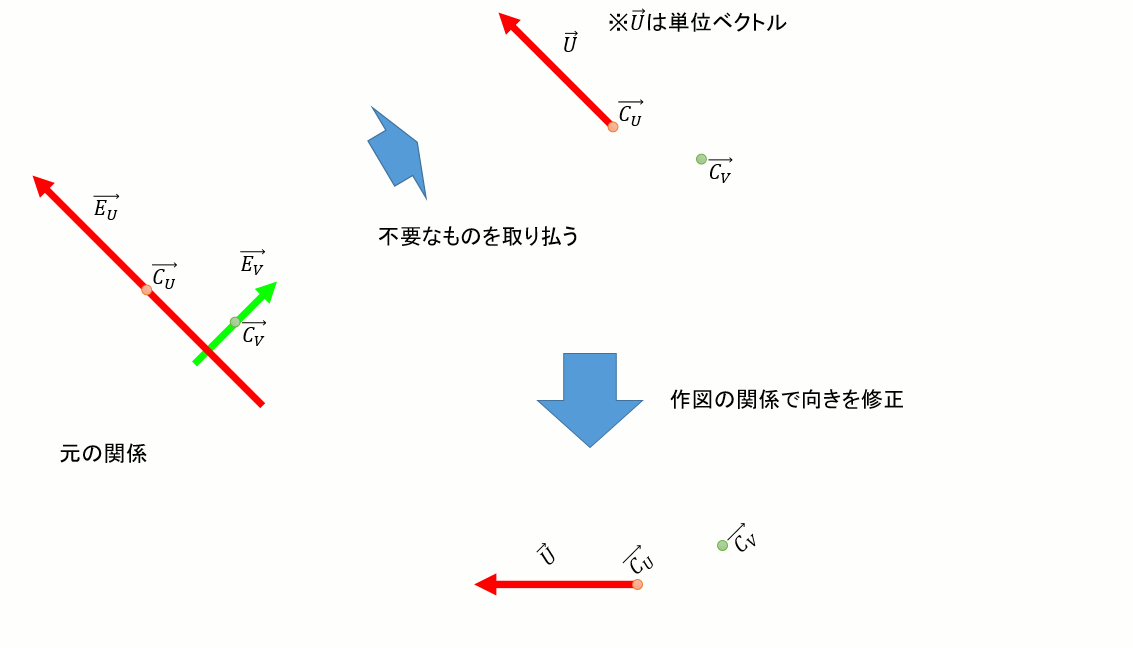
④ OBBの中央の算出
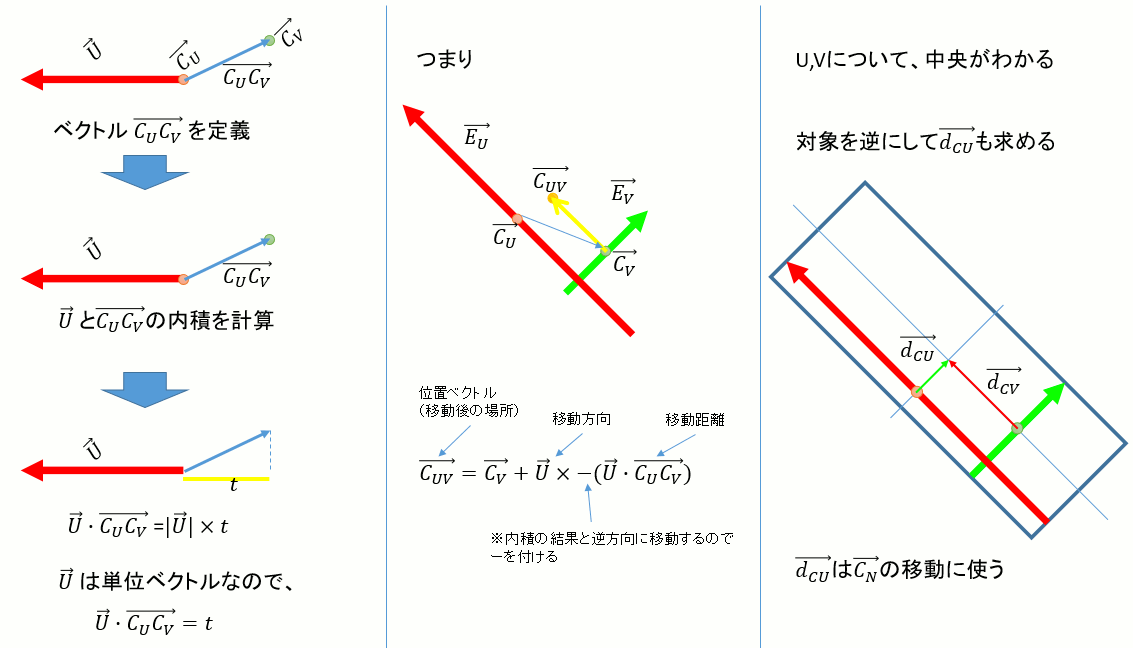
UV平面上の中央を求める
ここまでが上記参考文献の範疇なのだが、この→CU , →CV , →CN、実は一致しない。どうやら各辺の中央ではあるがボックスの中央ではないらしい。つまり以下のような関係になっていて、このまま辺の中央を使うわけにはいかない。
→U,→V,→N,→EU,→EV,→EN,→CU,→CV,→CN,からどうやってOBBの中央を求めればよいか。
以下のように、内積を使って移動量と方向を表す→dCU,→dCVを求める。
→CVに→dCVを加えるか、あるいは→CUに→dCUを加えれば、UV平面上のOBBの中央が求まる。
なんでこれで求まるのかは以下を参照:
https://www.studyplus.jp/467
【内積とは】ベクトルの内積の意味や公式・計算方法を知って大学合格へ!
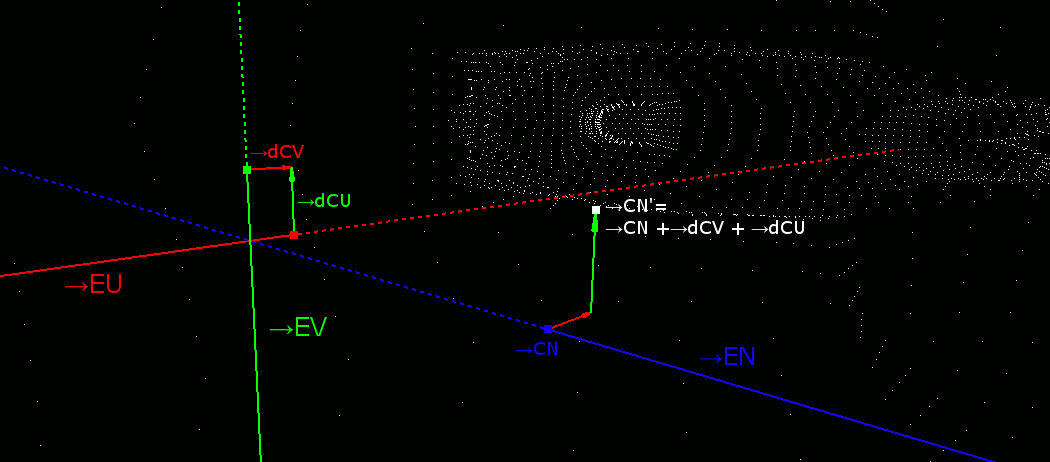
→CNを移動する
大変恐縮だが作図がもうめんどくさすぎるのでプログラムのSSで勘弁して欲しい。→CNの移動は、→CN' = →CN + →dCU+ →dCVとなる。
つまり、先ほどずっと計算していたUV平面と平行に移動する。
これでOBBの中央が求まった。
OBBの描画
OBBの中央が求まったら、そこから各方向の辺のベクトルの1/2を引けばOBBの端の点が求められる。
ソースコード
疲れたので次回。
Blender 雲(Volume)のチュートリアル抜粋
元は以下のチュートリアル:
なのだが無駄が多すぎる上に肝心な部分が瞬時に終わってしまうので抜粋する。なお同じ方向性でより優れたチュートリアルが複数あるので本来はそれを紹介したい。今回は手軽さを最優先にしている。
修正
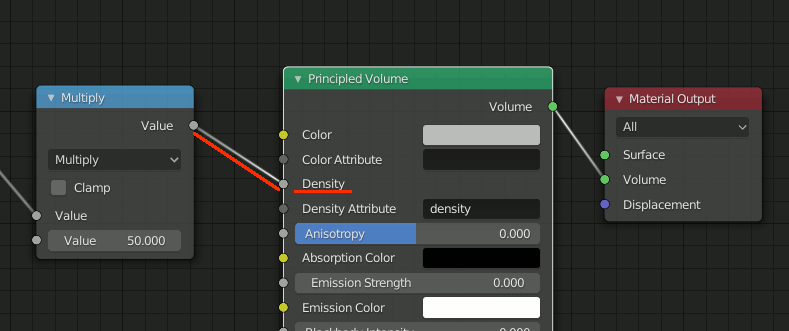
なお以降の画像中、Principled Volume側はDensityに接続する。
アップロードしてからミスに気づいたが修正する気力が無い。
手順
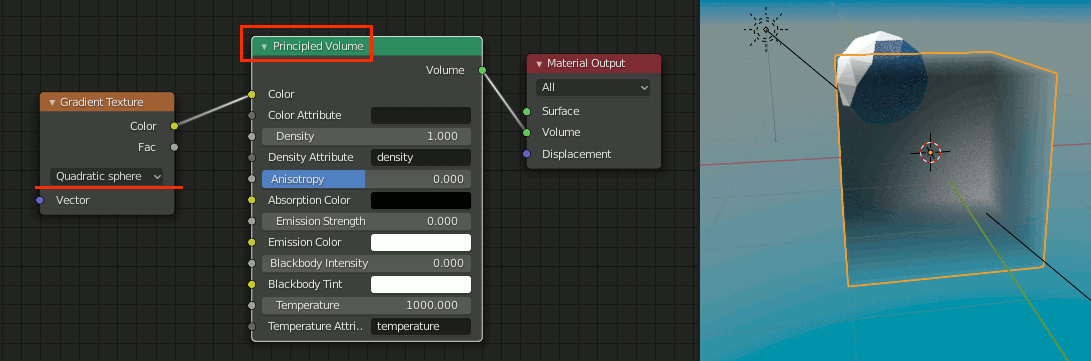
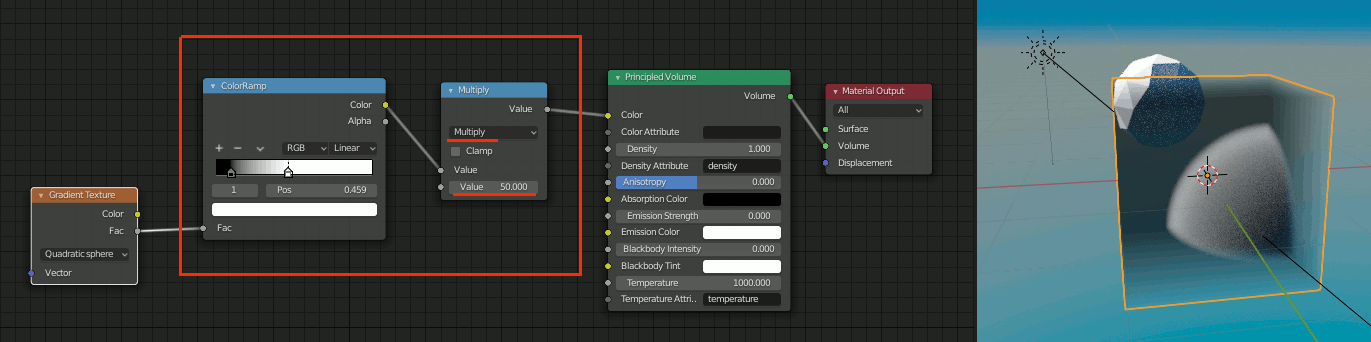
1.Principled Volume + Gradient Texture
[Shift+A]→[Texture]→[Gradient Texture]
[Shift+A]→[Shader]→Principled Volume
の二つを追加し、Gradient TextureをQuadratic sphereに設定
2. ColorRamp + Multiply
[Shift+A]→[Converter]→[ColorRamp]
[Shift+A]→[Converter]→[Math]
を追加し、MathをMultiplyに設定、ColorRampからの出力を50倍などの値に設定
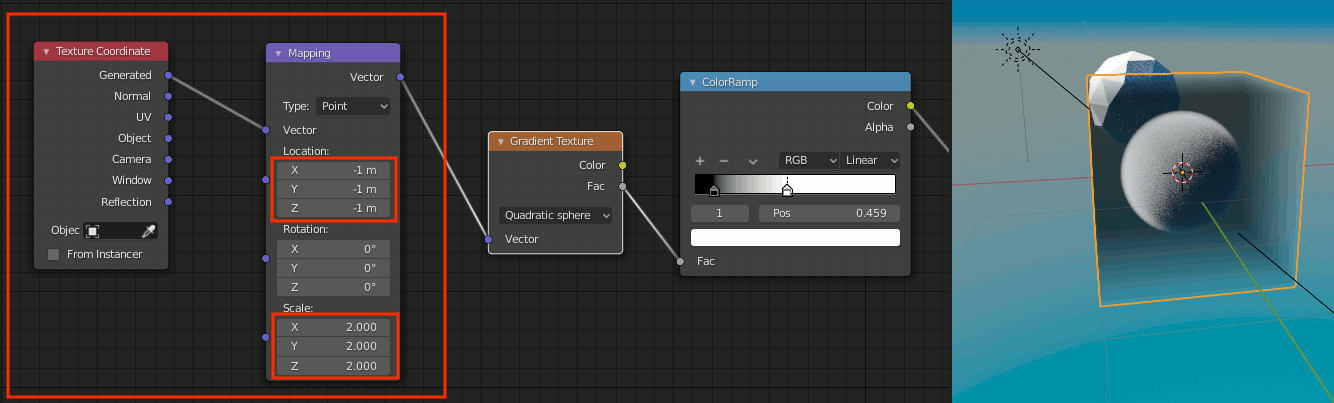
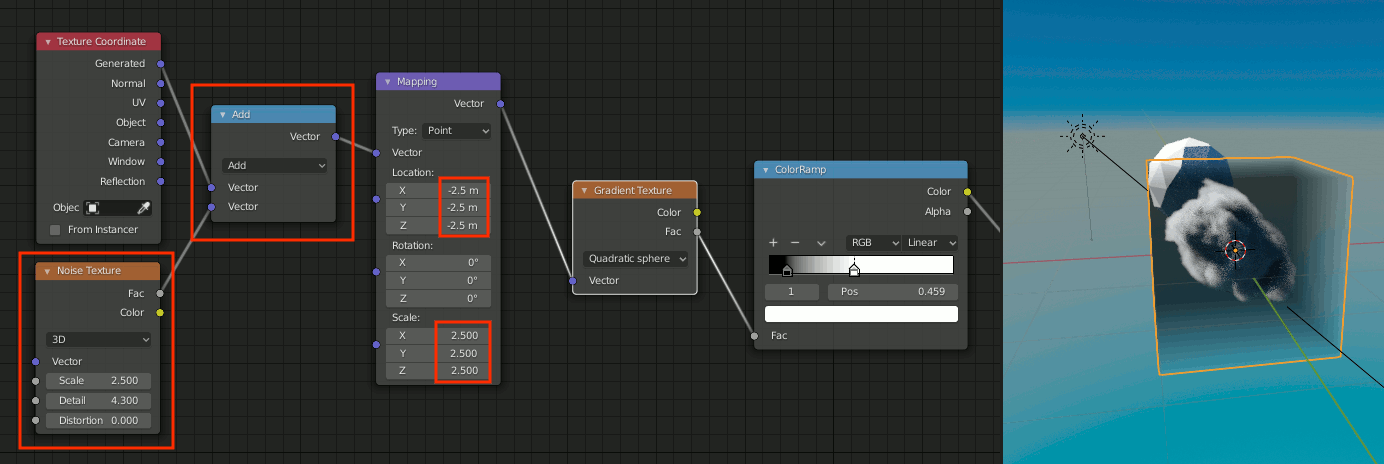
3. Texture Coordinate + Mapping追加
[Shift+A]→[input]→[Texture Coordinate]
[Shift+A]→[Vector]→[Mapping]
を追加し、MappingをLocationを(-1,-1,-1)、Scaleを(2,2,2)に設定する
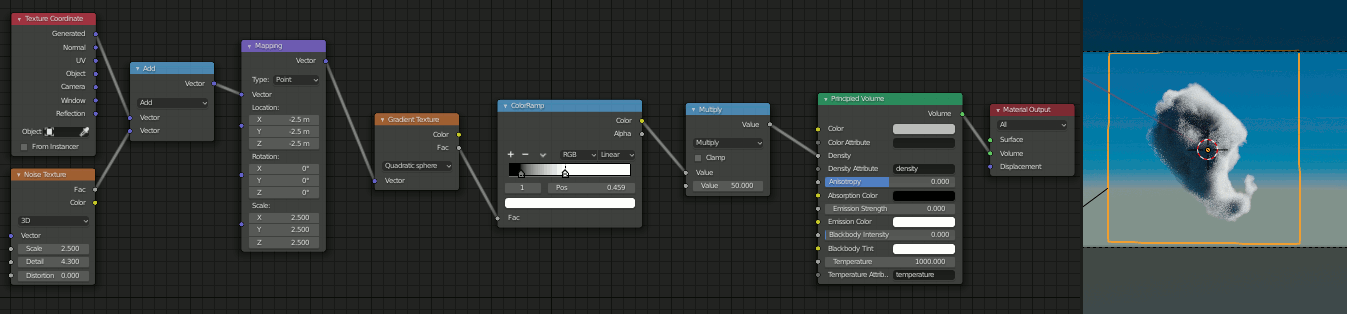
4. Noise Textureを加算
[Shift+A]→[Texture]→[Noise Texture]
[Shift+A]→[Converter]→[Vector Math]
をそれぞれ追加。
Texture CoordinateのGeneratedとNoise Textureを加算し、Mappingへ接続
Mapping側はLocationを(-2.5,-2.5,-2.5)、Scaleを(2.5,2.5,2.5)に変更
結果
BlenderでOSL
BlenderでOSLを使ってみる
作業の流れ
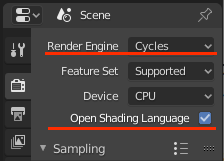
1.レンダラにCyclesを選択し、Open Shading Language にチェックを入れる
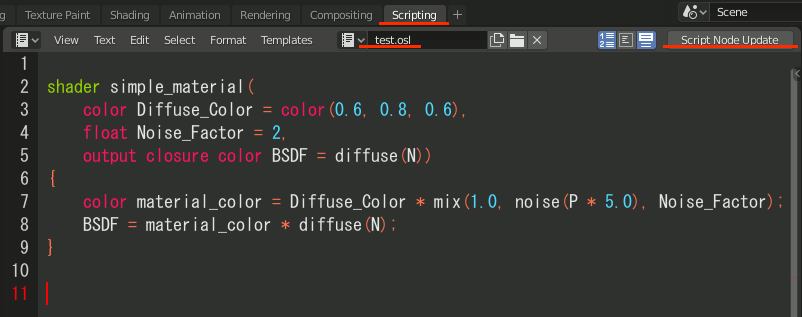
2.Scriptを書き、ファイル名を.oslの拡張子に変更、Script Node Updateをクリック
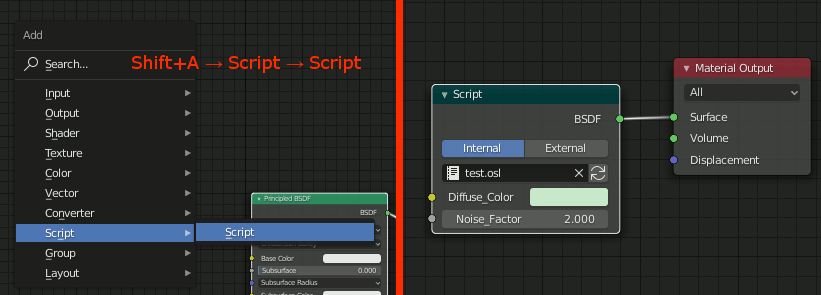
3.オブジェクトにマテリアルを設定、Shader EditorでScriptノードを追加、Material Outpuに連結
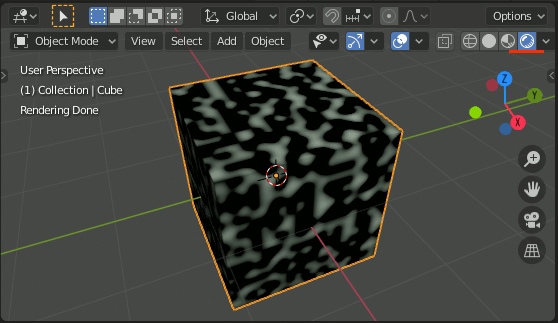
4.Viewport ShadingをRendered等にして結果を確認
詳細
1.レンダラにCyclesを選択し、Open Shading Language にチェックを入れる
2.Scriptを書き、ファイル名を.oslの拡張しに変更、Script Node Updateをクリック
プログラムは以下から。ただし結果がわかりやすいようにNoise_Factorの初期値とPの係数をわずかに変更している。
https://docs.blender.org/manual/ja/2.79/render/cycles/nodes/osl.html
3.オブジェクトにマテリアルを設定、Shader EditorでScriptノードを追加、Material Outpuに連結
4.Viewport ShadingをRendered等にして結果を確認
リンク
こちらのブログがものすごく重要な情報を纏めてくださっております。
公式のマニュアル
http://staffwww.itn.liu.se/~stegu/TNM084-2018/osl-languagespec.pdf
Googleリモートデスクトップのchromotingを停止
Windows 10でGoogleリモートデスクトップのサーバーなるとき、chromotingというサービスがインストールされ、常時起動するようになる。
調べた限りこいつが重大なセキュリティホールになるという話は見つからない。むしろ何らかの原因で停止したために接続できなくなった場合に起動方法を知っておこうという文脈の方が多い。
ただ個人的に、用途が明確にわかっていてかつ使わない遠隔操作用のサービスが動いているというのは気持ちが悪いので停止方法を調べた。
手順
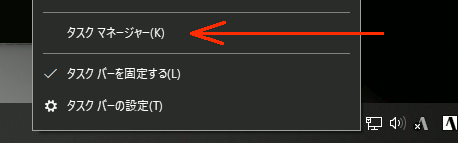
①タスクバーを右クリック→タスクマネージャ
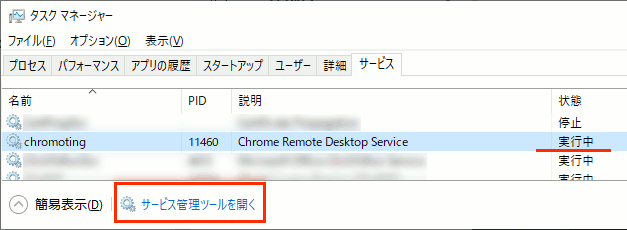
② "サービス" タグ → chromoting を見つけ、「実行中」になっている事を確認し、画面左下から、"サービス管理ツールを開く"
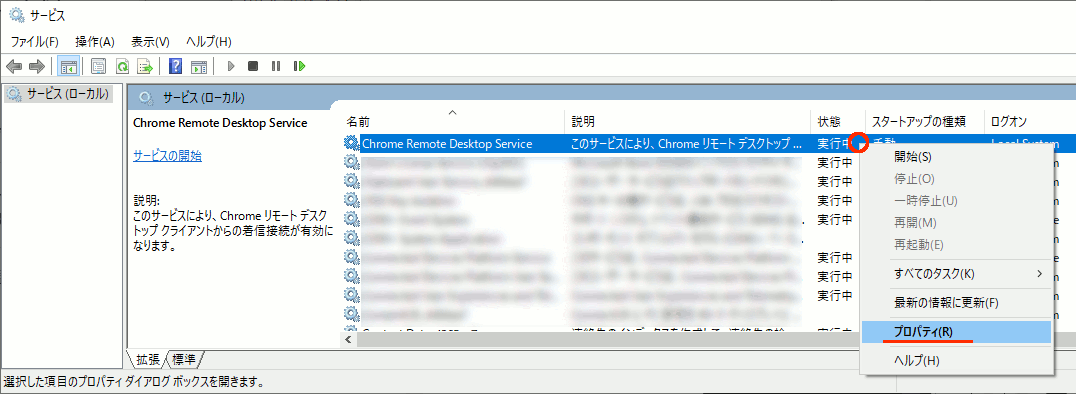
③ "Chrome Remote Desktop Service" を見つけ、右クリック → プロパティ
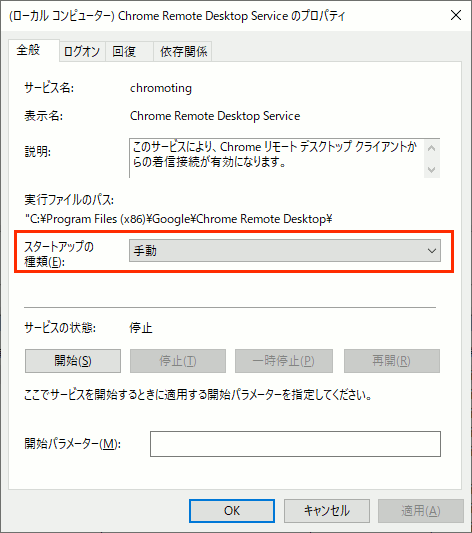
④ スタートアップの種類を「手動」または「無効」に設定
手動と無効の違い
・「手動」・・・サービスが必要になったときに勝手に実行され、サービスが不要になったときに勝手に停止する
・「停止」・・・ユーザが意図的に実行を指示しない限り動かない
手動だとサービスによっては停止したつもりでも殆ど起動しっぱなしという可能性もある。chromotingは見たところChromeを起動してChromeリモートデスクトップを使用中しか動かないように見えるが、不安なら「停止」にする。その代わり朝の忙しい時にリモートデスクトップの設定をする際に、chromotingの起動の手間が増える。
gluUnProjectを自前実装する
逆行列や行列の積に関しては以前の記事参照:
gluUnProjectもkhronosが言っている通りの式では結果が違ってしまうので実装例を確認してそちらに合わせた。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml
template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix44(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 4); } template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix_vec41(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 1); }
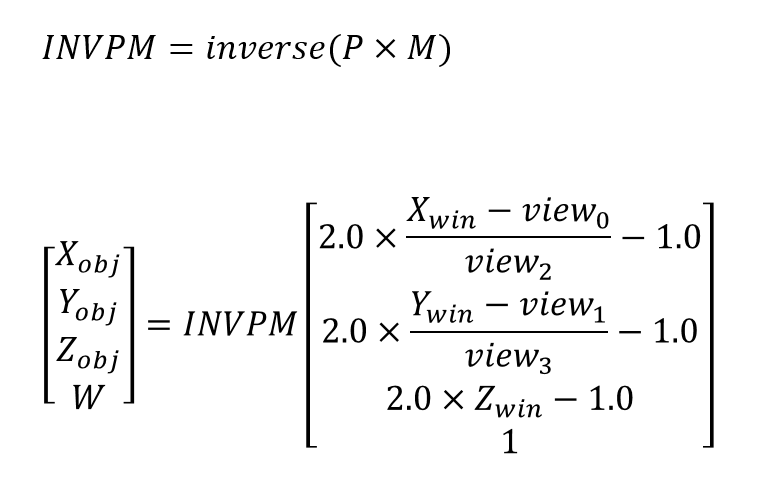
/////////////////////////////////////// // gluUnProject // https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml //! @brief gluUnProjectの自前実装版 //! @param [in] winX 画面上のX座標 //! @param [in] winY 画面上のY座標 //! @param [in] winZ 画面上のZ座標 //! @param [in] model モデルビュー行列 //! @param [in] proj プロジェクション行列 //! @param [in] ビューポート x,y,width,height //! @param [out] objX 空間座標のX //! @param [out] objY 空間座標のY //! @param [out] objZ 空間座標のZ //! @retval true 計算成功 //! @retval false 計算失敗
template<typename real_t> bool myUnProject( real_t winX, real_t winY, real_t winZ, const real_t* model, const real_t* proj, const int* view, real_t* objX, real_t* objY, real_t* objZ ) { real_t pm[16]; real_t invpm[16]; mult_matrix44(pm, proj, model);//pm = P×M bool ret = inverse_matrix44(invpm, pm);// pmの逆行列 if (ret == false) return false; real_t v[4] = { 2 * (winX - view[0]) / view[2] - 1.0 , 2 * (winY - view[1]) / view[3] - 1.0 , 2 * winZ - 1.0, 1 }; real_t vd[4]; mult_matrix_vec41(vd, invpm, v); // vd = invpm × v *objX = vd[0] / vd[3]; *objY = vd[1] / vd[3]; *objZ = vd[2] / vd[3]; return true; }
動作検証
int WIDTH = 300; int HEIGHT = 400; void disp(void) { glViewport(0, 0, WIDTH, HEIGHT); glMatrixMode(GL_PROJECTION); glPushMatrix(); glLoadIdentity(); gluPerspective(45, 0.5, 0.1, 2.5); glMatrixMode(GL_MODELVIEW); glPushMatrix(); glLoadIdentity(); glTranslated(-1, 0, -2); glRotated(1.5, 1.0, 1.0, 1.0);
////作成した変換行列を取得する GLdouble modeld[16]; glGetDoublev(GL_MODELVIEW_MATRIX, modeld); GLdouble projd[16]; glGetDoublev(GL_PROJECTION_MATRIX, projd); GLint view[4]; glGetIntegerv(GL_VIEWPORT, view);
// 三次元座標(出力) double objx, objy, objz; // 二次元ピクセル座標(入力) double winx = (rand() % 1000) / 100.0, winy = (rand() % 1000) / 100.0, winz = (rand() % 1000) / 100.0;
gluUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz); printf("glu %lf %lf %lf\n", objx, objy, objz);
myUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz ); printf("my %lf %lf %lf\n", objx, objy, objz);
puts("-----------"); glMatrixMode(GL_PROJECTION); glPopMatrix(); glMatrixMode(GL_MODELVIEW); glPopMatrix(); }
glu -1.165678 0.640021 1.701902 my -1.165678 0.640021 1.701902 ----------- glu -0.973079 0.946809 1.542299 my -0.973079 0.946809 1.542299 ----------- glu -0.734826 1.333922 1.296449 my -0.734826 1.333922 1.296449 ----------- glu -1.907228 1.907111 0.176182 my -1.907228 1.907111 0.176182 ----------- glu -1.917435 0.198937 1.894649 my -1.917435 0.198937 1.894649 ----------- glu -1.973992 0.975493 1.354121 my -1.973992 0.975493 1.354121 ----------- glu -1.364160 1.002119 1.417683 my -1.364160 1.002119 1.417683 ----------- glu -0.614162 0.527975 1.841761 my -0.614162 0.527975 1.841761 ----------- glu -0.323812 0.312351 1.947271 my -0.323812 0.312351 1.947271 -----------
gluProjectionを自前実装する
行列の積を自前実装できたのでgluProjectionを自前実装する。
数式
公式の式をそのまま使うとなぜか公式の結果と一致しない。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluProject.xml
実装例を見てみるとどうも式が若干違うのでそっちに合わせる。
http://collagefactory.blogspot.com/2010/03/gluproject-source-code.html
コード
//誤差の定義 template<typename T>struct real_error; template<>struct real_error<double> { static constexpr double value = 1e-15; }; template<>struct real_error<float> { static constexpr float value = (float)1e-7; }; //! @brief 誤差の閾値未満かをチェック //! @param [in] value 検査する値 //! @retval true 値の絶対値は閾値より小さい //! @retval false 値の絶対値は閾値より大きい template<typename T> inline bool is_error(const T value) { return abs(value) < real_error<T>::value; } //! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; } //! @brief IxJ行列 × JxK行列 の乗算関数 //https://suzulang.com/cpp-multmatrix44/ //! @param [out] C Cik 計算結果格納先 //! @param [in] A Aijの行列 //! @param [in] B Bjkの行列 //! @param [in] I Aの行列の行数 //! @param [in] J Aの行列の列数 //! @param [in] K Bの行列の列数 //! @return C template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrixIJK(real_tC* C, const real_tA* A, const real_tB* B, const int I, const int J, const int K) { for (int i = 0; i < I; i++) for (int k = 0; k < K; k++) { C[matijI(i, k, I)] = 0.0; for (int j = 0; j < J; j++) { C[matijI(i, k, I)] += A[matijI(i, j, I)] * B[matijI(j, k, J)]; } } return C; } template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix_vec41(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 1); }
// gluProject // https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluProject.xml // http://collagefactory.blogspot.com/2010/03/gluproject-source-code.html
//! @brief gluProjectの自前実装版 //! @param [in] wldX 空間座標のX //! @param [in] wldY 空間座標のY //! @param [in] wldZ 空間座標のZ //! @param [in] model モデルビュー行列 //! @param [in] proj プロジェクション行列 //! @param [in] ビューポート x,y,width,height //! @param [out] pixX 画面上のX座標 //! @param [out] pixY 画面上のY座標 //! @param [out] pixZ 画面上のZ座標 ※計算上は存在する //! @retval true 計算に成功 //! @retval false 計算に失敗 template<typename real_t> inline bool myProject( real_t wldX, real_t wldY, real_t wldZ, const real_t* model, const real_t* proj, const int* view, real_t* pixX, real_t* pixY, real_t* pixZ ) { real_t world[4] = { wldX,wldY,wldZ,1.0 }; real_t tmp[4]; real_t vdd[4]; mult_matrix_vec41(tmp, model, world); // tmp = M×v mult_matrix_vec41( vdd, proj, tmp ); // v'' = P×tmp if (is_error(vdd[3]) == true) return false; vdd[0] /= vdd[3]; vdd[1] /= vdd[3]; vdd[2] /= vdd[3]; //v''' = v'' / v''[3] *pixX = view[0] + view[2] * (vdd[0] + 1) / 2.0; *pixY = view[1] + view[3] * (vdd[1] + 1) / 2.0; *pixZ = (vdd[2] + 1) / 2.0; return true; }
動作チェック
gluProjectionと同じパラメータを入力し同じ結果が出るかを確認する。
テストコード
int WIDTH = 300; int HEIGHT = 400; void disp(void) { glViewport(0, 0, WIDTH, HEIGHT); glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity(); gluPerspective(45, 0.5, 0.1, 2.5); glMatrixMode(GL_MODELVIEW); glPushMatrix();
glLoadIdentity();
glTranslated(-1, 0, -2); glRotated(1.5, 1.0, 1.0, 1.0);
////作成した変換行列を取得する GLdouble modeld[16]; glGetDoublev(GL_MODELVIEW_MATRIX, modeld); GLdouble projd[16]; glGetDoublev(GL_PROJECTION_MATRIX, projd); GLint view[4]; glGetIntegerv(GL_VIEWPORT, view);
// 三次元座標(入力) double objx = (rand() % 1000) / 1000.0, objy = (rand() % 1000) / 1000.0, objz = (rand() % 1000) / 1000.0; // 二次元ピクセル座標(出力) double winx, winy, winz;
gluProject( objx, objy, objz, modeld, projd, view, &winx, &winy, &winz); printf("glu %lf %lf %lf\n", winx, winy, winz);
myProject(objx, objy, objz, modeld, projd, view, &winx, &winy, &winz); printf("my %lf %lf %lf\n", winx, winy, winz);
puts("-----------"); glMatrixMode(GL_PROJECTION); glPopMatrix(); glMatrixMode(GL_MODELVIEW); glPopMatrix(); }
実行結果
glu -269.362487 334.563333 0.978900
my -269.362487 334.563333 0.978900
-----------
glu -127.939462 262.458218 0.960356
my -127.939462 262.458218 0.960356
-----------
glu -207.160157 362.861399 0.941500
my -207.160157 362.861399 0.941500
-----------
glu -63.012933 385.110848 0.985399
my -63.012933 385.110848 0.985399
-----------
glu -353.644733 582.528452 0.940617
my -353.644733 582.528452 0.940617
-----------
glu -201.429535 654.202066 0.942501
my -201.429535 654.202066 0.942501
-----------
glu 72.061917 332.346399 0.977161
my 72.061917 332.346399 0.977161
-----------
glu -10.131515 438.149822 0.985127
my -10.131515 438.149822 0.985127
-----------