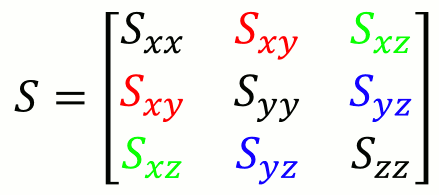スポンサーリンク
主成分分析で三次元点群から平面を求める – 1 – 分散共分散行列を求める
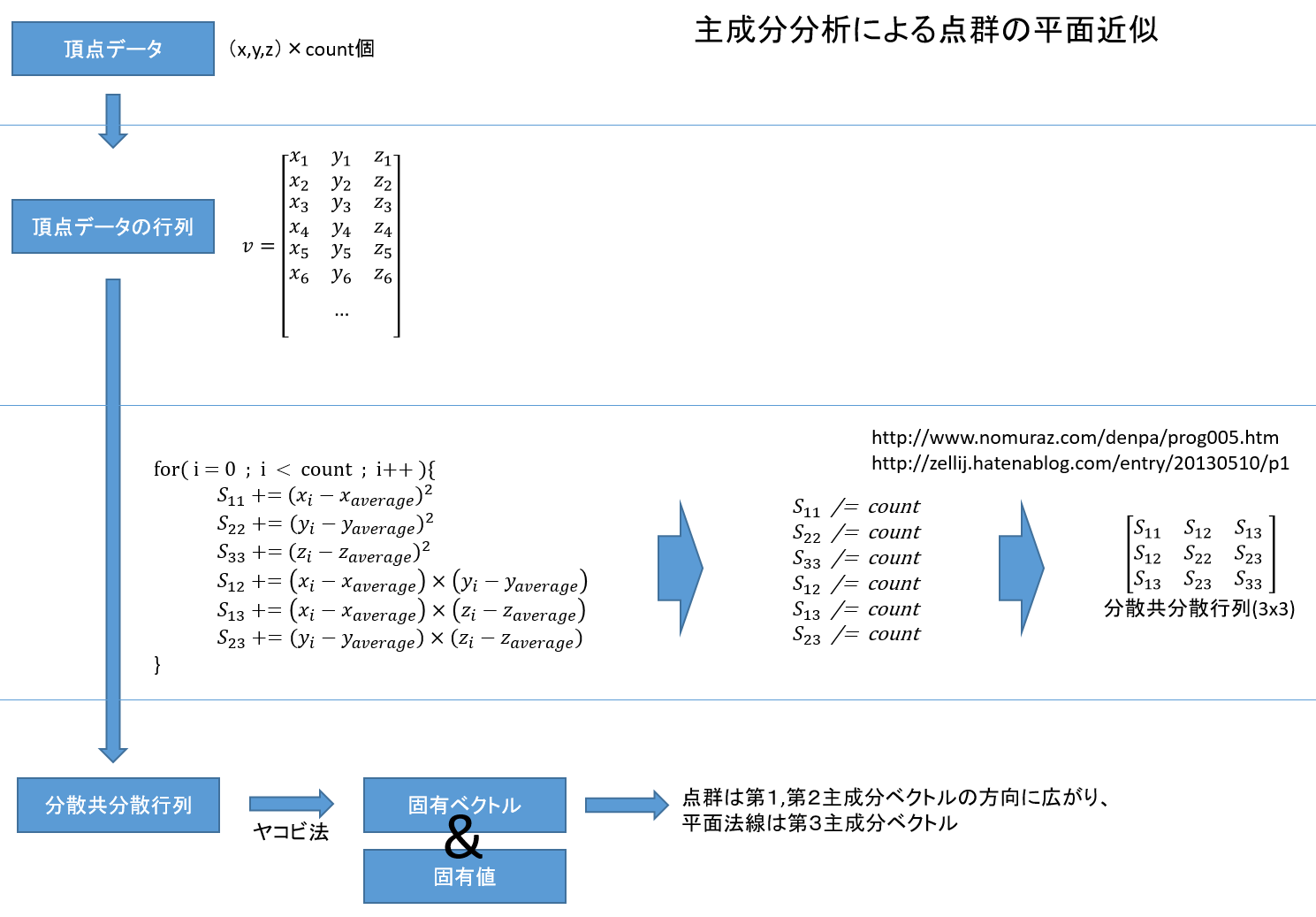
まず、手順としては下の図のようになる。
頂点データを行列として扱う所は特に問題は無いが、行列が苦手な人(自分もだが)のためにコメントすると3×頂点数の行列ができる。つまり例えば3×50000の行列とかにする。コード的な視点から見るとわざわざ「行列型」にする必要はない。構造体の配列で問題ない。
その行列に対して処理をして、最終的に3×3の分散共分散行列を作成する。その行列の固有ベクトル( xyzのベクトルが三つ )を求めればいい。
データ
例えば以下のようなデータの場合、分散共分散行列は3x3の行列になる。
| x | y | z |
|---|---|---|
| -0.9282366037368774 | -4.60659646987915 | 4.179419040679932 |
| -0.6398676633834839 | -4.345795631408691 | 3.8638782501220703 |
| -0.3469808101654053 | -4.115365028381348 | 3.5088584423065186 |
| -0.05463826656341553 | -3.881274938583374 | 3.1585941314697266 |
| 0.2328449785709381 | -3.614520311355591 | 2.850792646408081 |
| -1.0035791397094727 | -3.9636778831481934 | 3.8052620887756348 |
| -0.7170133590698242 | -3.690755844116211 | 3.5054771900177 |
| -0.4283676743507385 | -3.4318137168884277 | 3.1875195503234863 |
| -0.13146033883094788 | -3.2284107208251953 | 2.7973649501800537 |
| 0.15122388303279877 | -2.929394483566284 | 2.531501293182373 |
| -1.0883535146713257 | -3.2573564052581787 | 3.513524055480957 |
| -0.7981395721435547 | -3.0089566707611084 | 3.181861639022827 |
| -0.5119532346725464 | -2.733482599258423 | 2.88539457321167 |
| -0.21177172660827637 | -2.5520896911621094 | 2.466628313064575 |
| 0.08094996213912964 | -2.3205485343933105 | 2.113051414489746 |
| -1.1616857051849365 | -2.6279513835906982 | 3.1217992305755615 |
| -0.8680680990219116 | -2.402432918548584 | 2.7603931427001953 |
| -0.5798090696334839 | -2.140892267227173 | 2.4458136558532715 |
| -0.2915937602519989 | -1.87905752658844 | 2.1316158771514893 |
| 0.002897977828979492 | -1.6594164371490479 | 1.7625699043273926 |
| -1.2396777868270874 | -1.967220664024353 | 2.7707955837249756 |
| -0.9490185976028442 | -1.7218148708343506 | 2.43524169921875 |
| -0.6570032835006714 | -1.4855259656906128 | 2.087836503982544 |
| -0.36362549662590027 | -1.2583959102630615 | 1.7285257577896118 |
| -0.0764693021774292 | -0.9894416332244873 | 1.4235832691192627 |
分散共分散行列
分散共分散行列の形
データがx,y,zの場合、以下のような形をしている
問題はこのSxx,Sxy,Sxz,...をどうやって求めるかなのだが、このSxyは「xとyの共分散」である。
だから「xとxの共分散(=xの分散)」、「xとyの共分散」、...を求める。では共分散はどうやって求めるのか。
共分散の求め方
当然だが、Sxxの場合、「Sxx = (x[i]の偏差)の二乗の合計×(1/要素数)」になる。
偏差の求め方がわかれば共分散が求められ、共分散を求めることができれば分散共分散行列を組み立てることができる。
Excelで動作確認
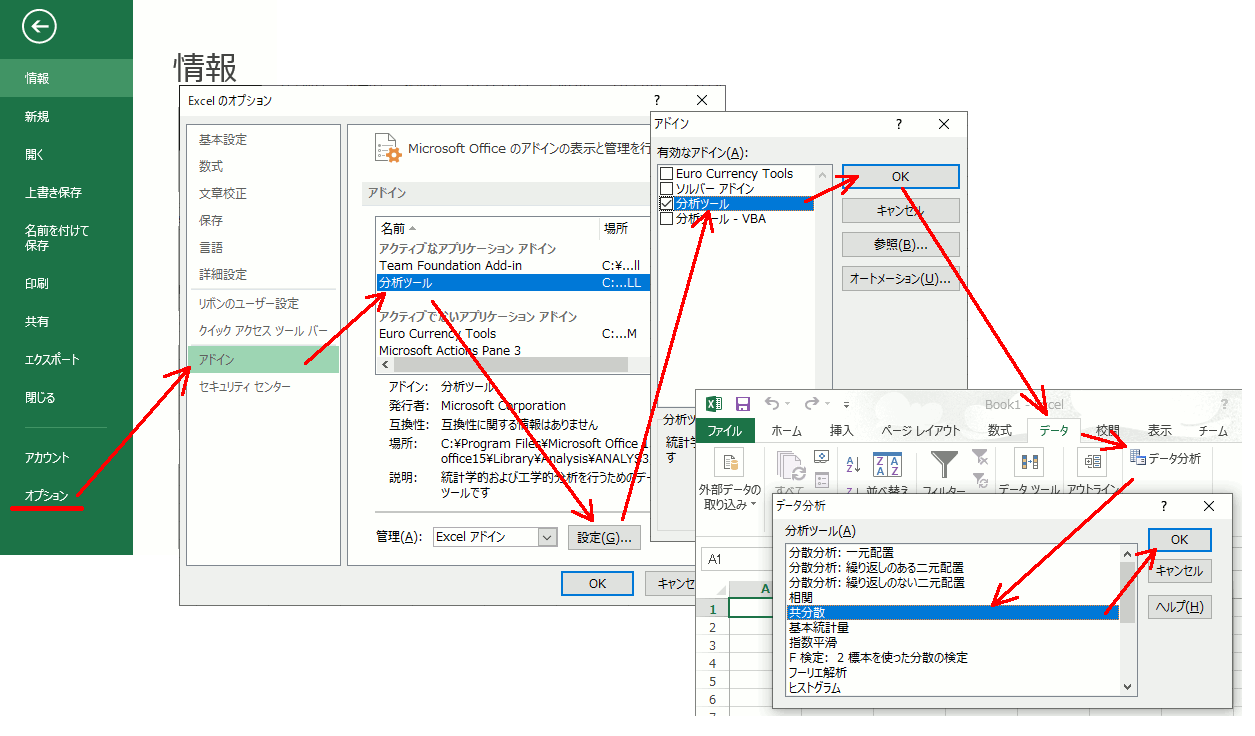
分析ツールの追加
プログラムに起こしたので、Excelに同じデータを入れて正しい答えが出ているかを確認する。
で分析ツールを追加し、データ→データ分析→共分散と操作する。
Excelによる計算結果
自作コードでの計算結果

ソースコード
#include <iostream> #include <vector> #include <array> //! @brief 座標を表すデータ型 struct point { double p[3]; point(double x, double y, double z) { p[0] = x; p[1] = y; p[2] = z; } point() {} };
//! @brief データの平均を求める //! @param [in] vec データの配列 //! @return 各要素の平均 point Covariance_Ave(const std::vector<point>& vec) { // 初期化 point ave; ave.p[0] = 0; ave.p[1] = 0; ave.p[2] = 0; // 各要素平均 for (size_t i = 0; i < vec.size(); i++) { ave.p[0] += vec[i].p[0]; ave.p[1] += vec[i].p[1]; ave.p[2] += vec[i].p[2]; } ave.p[0] /= vec.size(); ave.p[1] /= vec.size(); ave.p[2] /= vec.size(); return ave; }
//! @brief 共分散を求める //! @param [in] average 各要素の平均 //! @param [in] vec データ //! @param [in] param どの要素に対して求めるか。例えばxyzの時、x,yに対する共分散なら{0,1}を与える。 //! @return 偏差の積の和の要素数分の一 double Covariance(const point& average,const std::vector<point>& vec,const std::array<int,2>& param) { double sum = 0.0; for (size_t i = 0; i < vec.size(); i++) { //指定したパラメータの偏差を求める point deviation; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; deviation.p[target] = (vec[i].p[target] - average.p[target]); } //偏差の積 double product = 1.0; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; product *= deviation.p[target]; } //偏差の積の和を更新 sum += product; } //偏差の積の和のN分の一 return 1.0 / vec.size() * sum; }
void data(std::vector<point>& pt);
int main() { std::vector<point> pt; data( pt ); //データの準備 //各要素の平均を求める。 //これは共分散を求めるときに (x[i] - xの平均)×(y[i] - yの平均) 等の計算が必要なため point average = Covariance_Ave(pt); //共分散を求める //第三引数の{0,0}はxxを表す。xyなら{0,1}。これはデータがxyzの順に並んでいる事が前提。 double Sxx = Covariance(average, pt, { 0, 0 }); double Sxy = Covariance(average, pt, { 0, 1 }); double Sxz = Covariance(average, pt, { 0, 2 }); double Syy = Covariance(average, pt, { 1, 1 }); double Syz = Covariance(average, pt, { 1, 2 }); double Szz = Covariance(average, pt, { 2, 2 }); // 分散共分散行列を表示 printf("分散共分散行列\n"); printf("%.5lf %.5lf %.5lf\n", Sxx, Sxy, Sxz); printf("%.5lf %.5lf %.5lf\n", Sxy, Syy, Syz); printf("%.5lf %.5lf %.5lf\n", Sxz, Syz, Szz); int i; std::cin >> i; }
void data(std::vector<point>& pt) { pt.emplace_back(-0.9282366037368774, -4.60659646987915, 4.179419040679932); pt.emplace_back(-0.6398676633834839, -4.345795631408691, 3.8638782501220703); pt.emplace_back(-0.3469808101654053, -4.115365028381348, 3.5088584423065186); pt.emplace_back(-0.05463826656341553, -3.881274938583374, 3.1585941314697266); pt.emplace_back(0.2328449785709381, -3.614520311355591, 2.850792646408081); pt.emplace_back(-1.0035791397094727, -3.9636778831481934, 3.8052620887756348); pt.emplace_back(-0.7170133590698242, -3.690755844116211, 3.5054771900177); pt.emplace_back(-0.4283676743507385, -3.4318137168884277, 3.1875195503234863); pt.emplace_back(-0.13146033883094788, -3.2284107208251953, 2.7973649501800537); pt.emplace_back(0.15122388303279877, -2.929394483566284, 2.531501293182373); pt.emplace_back(-1.0883535146713257, -3.2573564052581787, 3.513524055480957); pt.emplace_back(-0.7981395721435547, -3.0089566707611084, 3.181861639022827); pt.emplace_back(-0.5119532346725464, -2.733482599258423, 2.88539457321167); pt.emplace_back(-0.21177172660827637, -2.5520896911621094, 2.466628313064575); pt.emplace_back(0.08094996213912964, -2.3205485343933105, 2.113051414489746); pt.emplace_back(-1.1616857051849365, -2.6279513835906982, 3.1217992305755615); pt.emplace_back(-0.8680680990219116, -2.402432918548584, 2.7603931427001953); pt.emplace_back(-0.5798090696334839, -2.140892267227173, 2.4458136558532715); pt.emplace_back(-0.2915937602519989, -1.87905752658844, 2.1316158771514893); pt.emplace_back(0.002897977828979492, -1.6594164371490479, 1.7625699043273926); pt.emplace_back(-1.2396777868270874, -1.967220664024353, 2.7707955837249756); pt.emplace_back(-0.9490185976028442, -1.7218148708343506, 2.43524169921875); pt.emplace_back(-0.6570032835006714, -1.4855259656906128, 2.087836503982544); pt.emplace_back(-0.36362549662590027, -1.2583959102630615, 1.7285257577896118); pt.emplace_back(-0.0764693021774292, -0.9894416332244873, 1.4235832691192627); }
参考
https://sci-pursuit.com/math/statistics/covariance.html
http://www.geisya.or.jp/~mwm48961/statistics/syuseibun1.htm
http://www.it.is.tohoku.ac.jp/lecture/pattern/pdf/2012/slide3.pdf
http://www.nomuraz.com/denpa/prog005.htm
http://sysplan.nams.kyushu-u.ac.jp/gen/edu/Algorithms/PlaneFitting/index.html
次回
固有ベクトルを求めるのだけれど、いかんせんヤコビ法が全く分からないので、その部分はコピペで済ます。
この記事のトラックバックURL: