月火水木金土日
glmのベクトル等のデータ型と関数を使って球とレイの交点を求めるプログラムを再考する
正直今更あまり意味がない(なぜあまり意味がないかは後日)のだが、以前つくった球とレイの交点を求めるプログラム。glm::vec使用版。画面をマウスドラッグで回転させたりするときに使ったりする。
cross.hpp
#pragma once #include <gl/glm-0.9.9/glm.hpp> #include <gl/glm-0.9.9/gtx/string_cast.hpp> #include <array> #include<vector> namespace szl {
template<typename T, size_t MAX>//最大二個まで結果を返せるようにしておく class LimitedArray { std::array<T, MAX> _data; size_t count; public: LimitedArray() :count(0) {} void push_back(const T& v) { if (count >= MAX) throw "count >= MAX"; _data[count++] = v; } void pop_back() { if (count == 0) throw "count == 0"; count--; } T& back() { if (count == 0) throw "count == 0"; return _data[count - 1]; } const T& back()const { return _data[count - 1]; } const T* data()const { return _data; } T* data() { return _data; } size_t size()const { return count; } const T& operator[](const size_t index)const { return _data[index]; } T& operator[](const size_t index) { return _data[index]; } };
struct HalfLineSegment { glm::vec3 S; // 始点 float t; // 長さ glm::vec3 V; // 方向 HalfLineSegment() {} HalfLineSegment(glm::vec3 _s, float _t, glm::vec3 _v) :S(_s), t(_t), V(_v) {} glm::vec3 E()const { return S + t * V; } };
//! @brief 球と直線の交点を求める
//! @param [in] center 球の中心
//! @param [in] r 球の半径
//! @param [in] from 直線上の点1
//! @param [in] to 直線状の点2
//! @return 座標値 0個 または 2個
// 参考 https://knzw.tech/raytracing/?page_id=78
LimitedArray< HalfLineSegment, 2> sphere_line_cross( const glm::vec3& center, const float r, const glm::vec3& from, const glm::vec3& to ) { LimitedArray< HalfLineSegment, 2> ret; //線分の始点をpで表す。 //球を0,0,0原点で計算するので、直線の方を球の中心分移動する glm::vec3 p = from - center; //直線の方程式を p + tvとする。 glm::vec3 v = to - from; float A = std::pow(glm::length(v), 2); float B = 2 * glm::dot(p, v); float C = std::pow(glm::length(p), 2) - r * r; float D = B * B - 4 * A * C; //判別式 float A2 = A * 2; if (D < 0.0) return ret; float sqrtD = std::sqrt(D); float t1 = (-B + sqrtD) / A2; float t2 = (-B - sqrtD) / A2; ret.push_back(HalfLineSegment(p + center, t1, v)); ret.push_back(HalfLineSegment(p + center, t2, v)); return ret; }
//! @brief 球と直線の交点を求めてfromに近い方の点を返す
//! @param [in] center 球の中心
//! @param [in] r 球の半径
//! @param [in] from 直線上の点1
//! @param [in] to 直線状の点2
//! @return 座標値
glm::vec3 sphere_line_hit( const glm::vec3& center, const float r, const glm::vec3& from, const glm::vec3& to ) { LimitedArray< HalfLineSegment, 2> hits = sphere_line_cross(center, r, from, to); glm::vec3 ret; switch (hits.size()) { case 1: ret = hits[0].E(); break; case 2: if (glm::distance(from, hits[0].E()) < glm::distance(from, hits[1].E())) { ret = hits[0].E(); } else { ret = hits[1].E(); } break; default: ret = glm::vec3{ std::numeric_limits<float>::infinity(), std::numeric_limits<float>::infinity(), std::numeric_limits<float>::infinity() }; } return ret; }
bool isValid(const glm::vec3& vec) { auto c = glm::isinf(vec); return c.x && c.y && c.z; }
}
テストコード
#include <iostream> #include "cross.hpp" int main() { // テスト値を設定 const glm::vec3 center{ -2.72692 ,-2.51743,3.0258 }; const float r= 2.44975f; const glm::vec3 from{ 1.69882,-1.63121,3.75584 }; const glm::vec3 to{ -7.42946 ,-4.48611 ,2.84412 }; // 交点を計算 auto hits = szl::sphere_line_cross(center, r, from, to); glm::vec3 P = szl::sphere_line_hit(center, r, from, to); // 結果を表示 std::cout << glm::to_string(P) << std::endl; std::cout << glm::to_string(hits[0].E()) << std::endl; std::cout << glm::to_string(hits[1].E()) << std::endl; }
出力
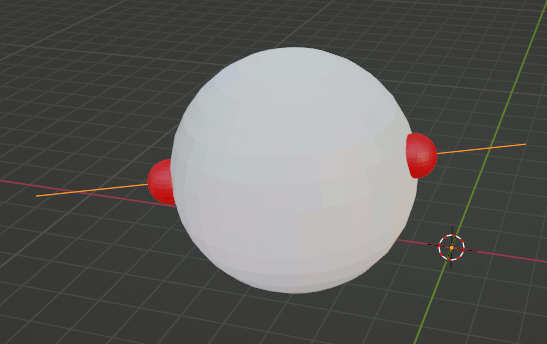
球と直線をBlenderで設定して、出力した座標に球を配置してみる。正しく計算できていることがわかる
vec3(-0.346963, -2.271036, 3.551510)
vec3(-4.877646, -3.688022, 3.098992)
vec3(-0.346963, -2.271036, 3.551510)
vec3(-4.877646, -3.688022, 3.098992)
vec3(-0.346963, -2.271036, 3.551510)