主成分分析で三次元点群から平面を求める – 2 – 固有ベクトルを求める

2020年7月19日公開
2020年7月30日更新

前回はデータから分散共分散行列を求めた。

分散共分散行列（3×3）に対してヤコビ法などを用いると、行列の固有値と固有ベクトルがそれぞれ３つずつ求まる。固有値が最も小さい固有ベクトルが面法線となる。

プログラム

リンク先、先頭のヤコビ法のプログラムをそのまま使用する

http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%B8%C7%CD%AD%C3%CD/%B8%C7%CD%AD%A5%D9%A5%AF%A5%C8%A5%EB

固有ベクトルと固有値

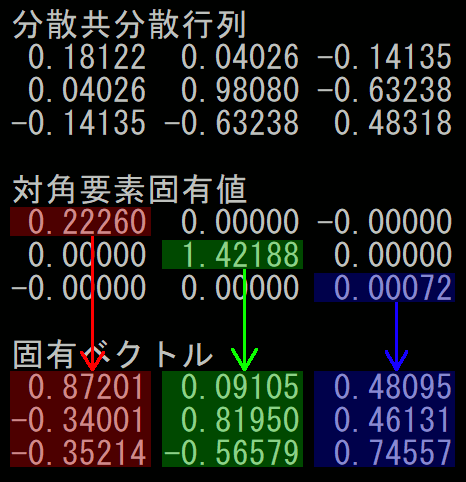
該当部分プログラム

  printf("分散共分散行列\n");
  printf("% 1.5lf % 1.5lf % 1.5lf\n", Sxx, Sxy, Sxz);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", Sxy, Syy, Syz);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", Sxz, Syz, Szz);
  puts("");

  float a[3 * 3] = {
    Sxx,Sxy,Sxz,
    Sxy,Syy,Syz,
    Sxz,Syz,Szz
  };
  float v[3 * 3];
  EigenJacobiMethod(a, v, 3);

  printf("対角要素固有値\n");
  printf("% 1.5lf % 1.5lf % 1.5lf\n", a[0], a[1], a[2]);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", a[3], a[4], a[5]);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", a[6], a[7], a[8]);
  puts("");
  printf("固有ベクトル\n");
  printf("% 1.5lf % 1.5lf % 1.5lf\n", v[0], v[1], v[2]);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", v[3], v[4], v[5]);
  printf("% 1.5lf % 1.5lf % 1.5lf\n", v[6], v[7], v[8]);

面法線の選択

主成分分析で得られるベクトルは、データがどの方向にばらついているかを表していて、一番ばらつきが少ない方向が面法線という事になる

参考：

主成分分析の考え方

ので、一番小さい固有値に対応した固有ベクトルが面法線になる。

参考：

”主成分分析における固有値は、その固有ベクトルの方向に沿ったデータの分散の大きさに対応します。固有値が大きい固有ベクトルほど、データの分散をよく説明している、つまり、データの重要な特徴を捉えていると考えられます。なので、各固有値を固有値の合計で割ったものを寄与率と呼んだり、固有値（寄与率）が大きい主成分から順に、第１主成分（PC1）、第２主成分（PC2）……と呼んだりします。”

https://qiita.com/animegazer/items/c7d99d6d1dee2f3f936f

上記結果では固有値が0.00072のベクトル( 0.00957 , -0.00150 , 0.99995 )が答えになる。

面の特定

面はその面に含まれる一点と法線ベクトルがわかれば求められる。

面に含まれる一点・・・頂点群の重心

面法線・・・頂点群の主成分分析の結果の第三主成分

で面が決定できる。

プログラム全体

#include <iostream>
#include <vector>
#include <array>

//! @struct point
//! @brief 座標を表すデータ型
struct point {
  double p[3];
  point(double x, double y, double z) {
    p[0] = x;
    p[1] = y;
    p[2] = z;
  }
  point() {}
};
//! @brief 固有値・固有ベクトル
struct eigen {
  double val;   //!< 固有値
  double vec[3];//!< 固有ベクトル
};


int EigenJacobiMethod(float* a, float* v, int n, float eps = 1e-8, int iter_max = 100);

void data(std::vector<point>& pt);

//! @brief データの平均を求める
//! @param [in] vec データの配列
//! @return 各要素の平均
point Covariance_Ave(const std::vector<point>& vec) {

  // 初期化
  point ave;
  ave.p[0] = 0;
  ave.p[1] = 0;
  ave.p[2] = 0;

  // 各要素平均
  for (size_t i = 0; i < vec.size(); i++) {
    ave.p[0] += vec[i].p[0];
    ave.p[1] += vec[i].p[1];
    ave.p[2] += vec[i].p[2];
  }
  ave.p[0] /= vec.size();
  ave.p[1] /= vec.size();
  ave.p[2] /= vec.size();

  return ave;

}

//! @brief 共分散を求める
//! @param [in] average 各要素の平均
//! @param [in] vec データ
//! @param [in] param どの要素に対して求めるか。例えばxyzの時、x,yに対する共分散なら{0,1}を与える。
//! @return 偏差の積の和の要素数分の一
double Covariance(const point& average,const std::vector<point>& vec,const std::array<int,2>& param) {

  double sum = 0.0;
  for (size_t i = 0; i < vec.size(); i++) {

    //指定したパラメータの偏差を求める
    point deviation;
    for (size_t j = 0; j < param.size(); j++) {
      int target = param[j];
      deviation.p[target] = (vec[i].p[target] - average.p[target]);
    }

    //偏差の積
    double product = 1.0;
    for (size_t j = 0; j < param.size(); j++) {
      int target = param[j];
      product *= deviation.p[target];
    }

    //偏差の積の和を更新
    sum += product;
  }

  //偏差の積の和のN分の一
  return 1.0 / vec.size() * sum;
}

//! @brief データを主成分分析する
//! @param [out] ev 固有値と固有ベクトル
//! @param [in] average 全データの各要素の平均
//! @param [in] pt 三次元の座標値一覧
//! @return なし
void eigen_vector(eigen* ev, point* average, const std::vector<point>& pt) {

  //各要素の平均を求める。
  //これは共分散を求めるときに (x[i] - xの平均)×(y[i] - yの平均) 等の計算が必要なため
  *average = Covariance_Ave(pt);

  //共分散を求める
  //第三引数の{0,0}はxxを表す。xyなら{0,1}。これはデータがxyzの順に並んでいる事が前提。
  double Sxx = Covariance(*average, pt, { 0, 0 });
  double Sxy = Covariance(*average, pt, { 0, 1 });
  double Sxz = Covariance(*average, pt, { 0, 2 });
  double Syy = Covariance(*average, pt, { 1, 1 });
  double Syz = Covariance(*average, pt, { 1, 2 });
  double Szz = Covariance(*average, pt, { 2, 2 });


  // 分散共分散行列
  float a[3 * 3] = {
    Sxx,Sxy,Sxz,
    Sxy,Syy,Syz,
    Sxz,Syz,Szz
  };


  float v[3 * 3];
  EigenJacobiMethod(a, v, 3);

  ev[0].val = a[0];   //固有値
  ev[0].vec[0] = v[0];//固有値に対応した固有ベクトル
  ev[0].vec[1] = v[3];
  ev[0].vec[2] = v[6];

  ev[1].val = a[4];   //固有値
  ev[1].vec[0] = v[1];//固有値に対応した固有ベクトル
  ev[1].vec[1] = v[4];
  ev[1].vec[2] = v[7];

  ev[2].val = a[8];   //固有値
  ev[2].vec[0] = v[2];//固有値に対応した固有ベクトル
  ev[2].vec[1] = v[5];
  ev[2].vec[2] = v[8];


}

int main()
{

  std::vector<point> pt;

  data( pt );

  //データの準備

  eigen ev[3];
  point average;
  eigen_vector(ev, &average,pt);

  //固有値と固有ベクトルを表示
  printf("[%lf] %lf %lf %lf\n", ev[0].val, ev[0].vec[0], ev[0].vec[1], ev[0].vec[2]);
  printf("[%lf] %lf %lf %lf\n", ev[1].val, ev[1].vec[0], ev[1].vec[1], ev[1].vec[2]);
  printf("[%lf] %lf %lf %lf\n", ev[2].val, ev[2].vec[0], ev[2].vec[1], ev[2].vec[2]);

  printf("\n重心\n");
  printf("%.5lf %.5lf %.5lf\n", average.p[0], average.p[1], average.p[2]);

  int i;
  std::cin >> i;

}

void data(std::vector<point>& pt) {

  pt.emplace_back(-0.9282366037368774, -4.60659646987915, 4.179419040679932);
  pt.emplace_back(-0.6398676633834839, -4.345795631408691, 3.8638782501220703);
  pt.emplace_back(-0.3469808101654053, -4.115365028381348, 3.5088584423065186);
  pt.emplace_back(-0.05463826656341553, -3.881274938583374, 3.1585941314697266);
  pt.emplace_back(0.2328449785709381, -3.614520311355591, 2.850792646408081);
  pt.emplace_back(-1.0035791397094727, -3.9636778831481934, 3.8052620887756348);
  pt.emplace_back(-0.7170133590698242, -3.690755844116211, 3.5054771900177);
  pt.emplace_back(-0.4283676743507385, -3.4318137168884277, 3.1875195503234863);
  pt.emplace_back(-0.13146033883094788, -3.2284107208251953, 2.7973649501800537);
  pt.emplace_back(0.15122388303279877, -2.929394483566284, 2.531501293182373);
  pt.emplace_back(-1.0883535146713257, -3.2573564052581787, 3.513524055480957);
  pt.emplace_back(-0.7981395721435547, -3.0089566707611084, 3.181861639022827);
  pt.emplace_back(-0.5119532346725464, -2.733482599258423, 2.88539457321167);
  pt.emplace_back(-0.21177172660827637, -2.5520896911621094, 2.466628313064575);
  pt.emplace_back(0.08094996213912964, -2.3205485343933105, 2.113051414489746);
  pt.emplace_back(-1.1616857051849365, -2.6279513835906982, 3.1217992305755615);
  pt.emplace_back(-0.8680680990219116, -2.402432918548584, 2.7603931427001953);
  pt.emplace_back(-0.5798090696334839, -2.140892267227173, 2.4458136558532715);
  pt.emplace_back(-0.2915937602519989, -1.87905752658844, 2.1316158771514893);
  pt.emplace_back(0.002897977828979492, -1.6594164371490479, 1.7625699043273926);
  pt.emplace_back(-1.2396777868270874, -1.967220664024353, 2.7707955837249756);
  pt.emplace_back(-0.9490185976028442, -1.7218148708343506, 2.43524169921875);
  pt.emplace_back(-0.6570032835006714, -1.4855259656906128, 2.087836503982544);
  pt.emplace_back(-0.36362549662590027, -1.2583959102630615, 1.7285257577896118);
  pt.emplace_back(-0.0764693021774292, -0.9894416332244873, 1.4235832691192627);

}

/*!
 * Jacobi法による固有値の算出
 * @param[inout] a 実対称行列．計算後，対角要素に固有値が入る
 * @param[out] v 固有ベクトル(aと同じサイズ)
 * @param[in] n 行列のサイズ(n×n)
 * @param[in] eps 収束誤差
 * @param[in] iter_max 最大反復回数
 * @return 反復回数
 * @see http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%B8%C7%CD%AD%C3%CD/%B8%C7%CD%AD%A5%D9%A5%AF%A5%C8%A5%EB
 */
int EigenJacobiMethod(float* a, float* v, int n, float eps, int iter_max)
{
  float* bim, * bjm;
  float bii, bij, bjj, bji;

  bim = new float[n];
  bjm = new float[n];

  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
      v[i * n + j] = (i == j) ? 1.0 : 0.0;
    }
  }

  int cnt = 0;
  for (;;) {
    int i, j;

    float x = 0.0;
    for (int ia = 0; ia < n; ++ia) {
      for (int ja = 0; ja < n; ++ja) {
        int idx = ia * n + ja;
        if (ia != ja && fabs(a[idx]) > x) {
          i = ia;
          j = ja;
          x = fabs(a[idx]);
        }
      }
    }

    float aii = a[i * n + i];
    float ajj = a[j * n + j];
    float aij = a[i * n + j];

    float alpha, beta;
    alpha = (aii - ajj) / 2.0;
    beta = sqrt(alpha * alpha + aij * aij);

    float st, ct;
    ct = sqrt((1.0 + fabs(alpha) / beta) / 2.0);    // sinθ
    st = (((aii - ajj) >= 0.0) ? 1.0 : -1.0) * aij / (2.0 * beta * ct);    // cosθ

    // A = PAPの計算
    for (int m = 0; m < n; ++m) {
      if (m == i || m == j) continue;

      float aim = a[i * n + m];
      float ajm = a[j * n + m];

      bim[m] = aim * ct + ajm * st;
      bjm[m] = -aim * st + ajm * ct;
    }

    bii = aii * ct * ct + 2.0 * aij * ct * st + ajj * st * st;
    bij = 0.0;

    bjj = aii * st * st - 2.0 * aij * ct * st + ajj * ct * ct;
    bji = 0.0;

    for (int m = 0; m < n; ++m) {
      a[i * n + m] = a[m * n + i] = bim[m];
      a[j * n + m] = a[m * n + j] = bjm[m];
    }
    a[i * n + i] = bii;
    a[i * n + j] = bij;
    a[j * n + j] = bjj;
    a[j * n + i] = bji;

    // V = PVの計算
    for (int m = 0; m < n; ++m) {
      float vmi = v[m * n + i];
      float vmj = v[m * n + j];

      bim[m] = vmi * ct + vmj * st;
      bjm[m] = -vmi * st + vmj * ct;
    }
    for (int m = 0; m < n; ++m) {
      v[m * n + i] = bim[m];
      v[m * n + j] = bjm[m];
    }

    float e = 0.0;
    for (int ja = 0; ja < n; ++ja) {
      for (int ia = 0; ia < n; ++ia) {
        if (ia != ja) {
          e += fabs(a[ja * n + ia]);
        }
      }
    }
    if (e < eps) break;

    cnt++;
    if (cnt > iter_max) break;
  }

  delete[] bim;
  delete[] bjm;

  return cnt;
}

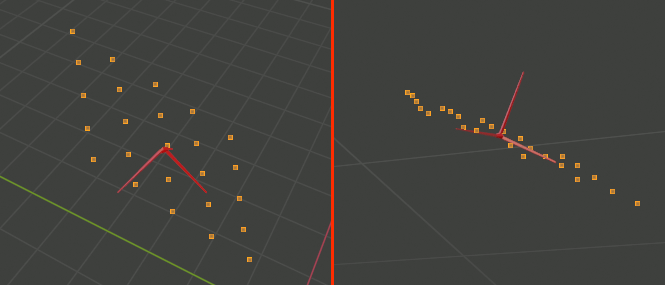
Blenderで可視化

もっと良いツールがあるのかもしれないがＢｌｅｎｄｅｒで重心から各主成分に線を伸ばしたものを作成して結果を確認する

コメントを残すコメントをキャンセル

この記事のトラックバックURL：