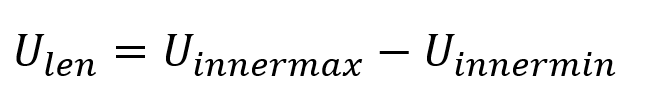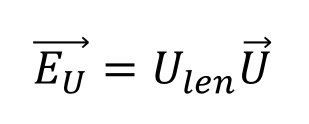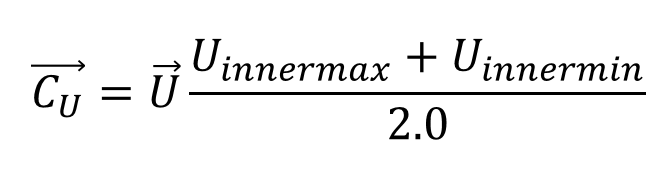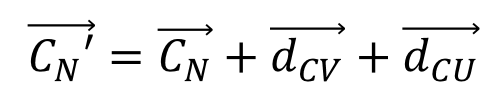OBBを計算する(計算方法)
OBBとAABB
OBBは物体を最小で囲むBoundingBoxの事で、無駄なく囲めるが求めるのが難しい。
AABBは物体のX軸Y軸Z軸の最大-最小からなるBoundingBoxで、求めるのがきわめて簡単だが無駄が多い。
主成分分析
以前、主成分分析で点群の法線を求めた。三次元の点群に主成分分析をかけた結果出てきた第一、第二、第三主成分を使えばOBBが求められる。
参考文献
以下のサイトをなぞっていく。
http://www.nomuraz.com/denpa/prog005.htm
手順
① OBBの各辺の方向を求める
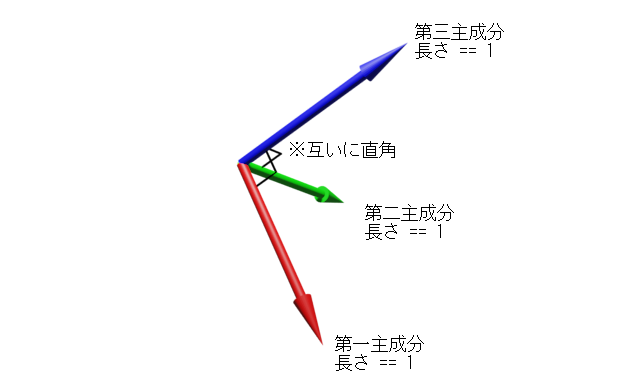
三次元点群データを主成分分析すると、固有ベクトルが三つ(第一、第二、第三主成分)得られる。
この三つのベクトルは互いに垂直で且つ長さが1になっている。
この各ベクトルが、OBBの各辺の方向となる。
つまり、各辺の方向は主成分分析の結果そのものである。
面の抽出の時は広がりの一番小さい方向を表す第三主成分を使ったがOBBの時は三つとも使うことになる。
以下、各ベクトルを→U , →V , →N とする。
② OBBの各辺の長さ
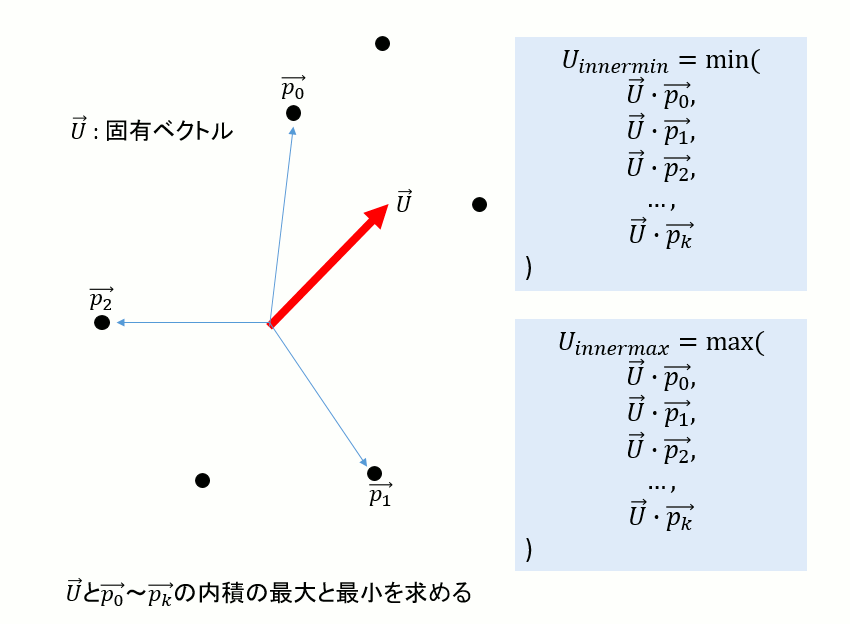
方向がわかったので次は辺の長さを求める。
まず、固有ベクトルについて、そのベクトルとすべての頂点座標(位置ベクトル)の内積をとり、その最大・最小を求める。
こうして求めたU,V,Nの(max-min)の値が、各方向の辺の長さとなる
この計算を、→U , →V , →N それぞれについて行う。
そして、OBBの辺としての長さがわかったので、各辺をベクトルで表すと、
これでエッジの長さと方向を表す→EU , →EV , →ENが求められた。
③ OBBの各辺の中央
各内積の最大と最小を足して2で割り、各ベクトルを掛けると、各辺の中央が求められる
この計算も、→U , →V , →N それぞれについて行う。
これを→CU , →CV , →CNとする。
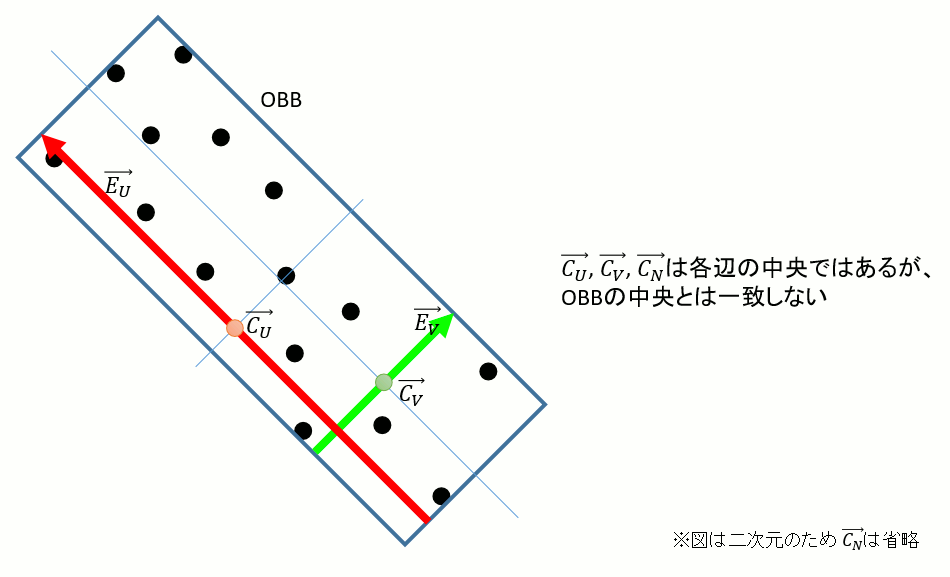
④ OBBの中央の算出
UV平面上の中央を求める
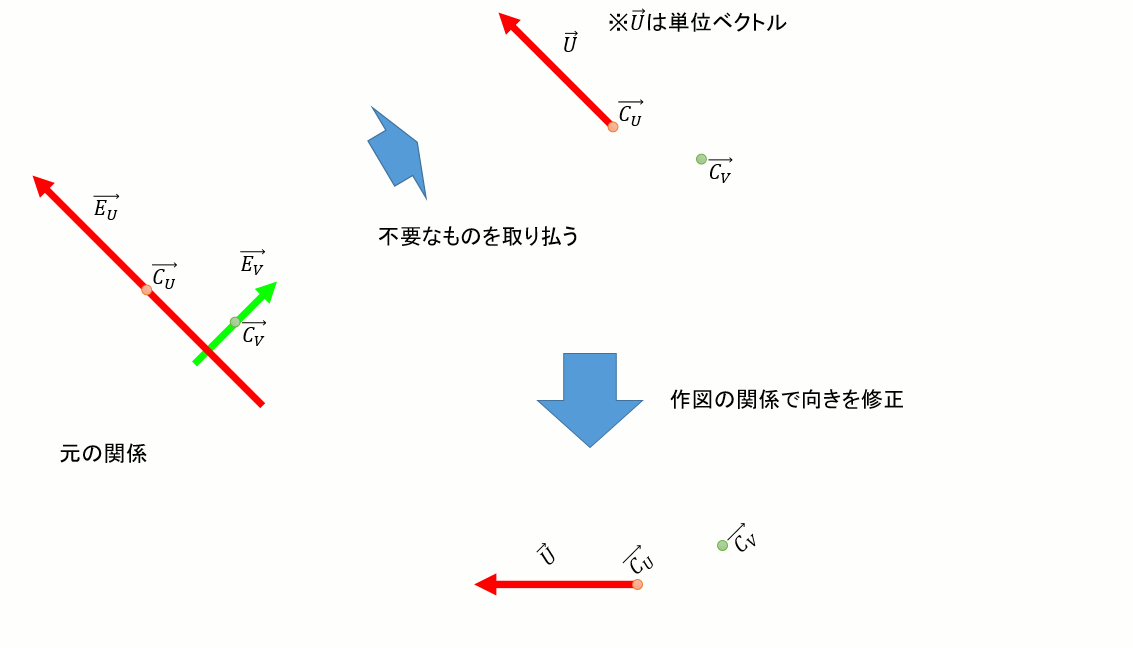
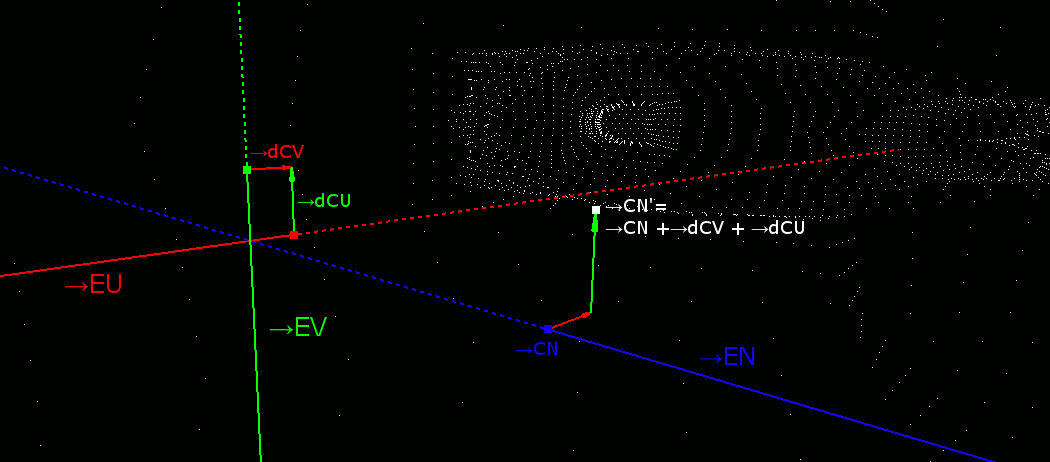
ここまでが上記参考文献の範疇なのだが、この→CU , →CV , →CN、実は一致しない。どうやら各辺の中央ではあるがボックスの中央ではないらしい。つまり以下のような関係になっていて、このまま辺の中央を使うわけにはいかない。
→U,→V,→N,→EU,→EV,→EN,→CU,→CV,→CN,からどうやってOBBの中央を求めればよいか。
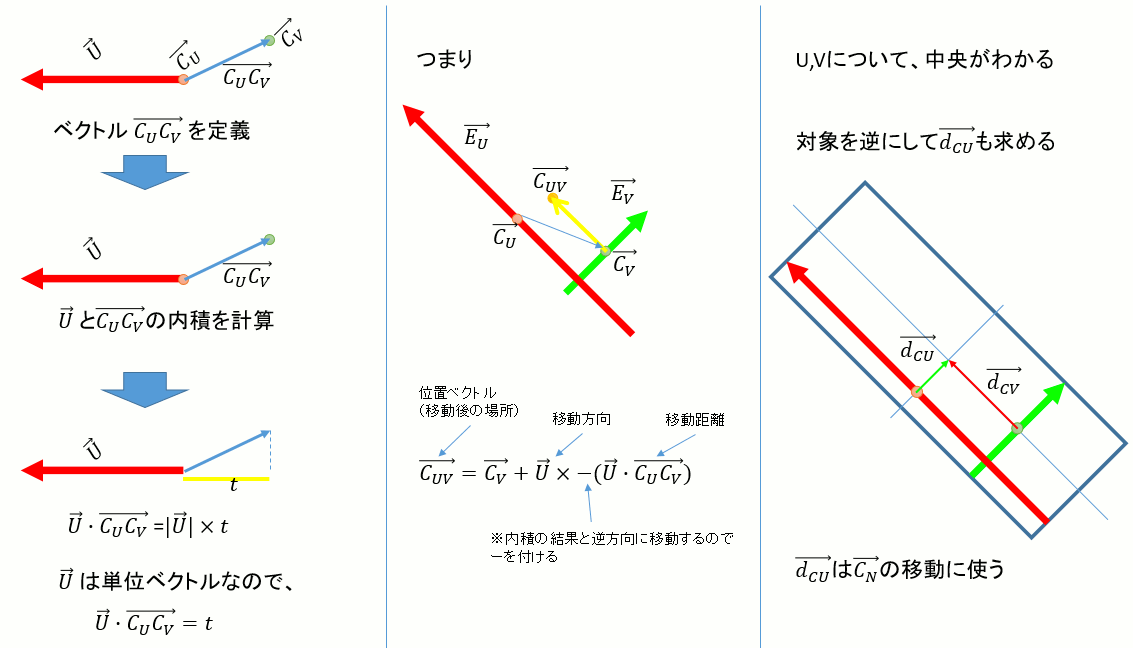
以下のように、内積を使って移動量と方向を表す→dCU,→dCVを求める。
→CVに→dCVを加えるか、あるいは→CUに→dCUを加えれば、UV平面上のOBBの中央が求まる。
なんでこれで求まるのかは以下を参照:
https://www.studyplus.jp/467
【内積とは】ベクトルの内積の意味や公式・計算方法を知って大学合格へ!
→CNを移動する
大変恐縮だが作図がもうめんどくさすぎるのでプログラムのSSで勘弁して欲しい。→CNの移動は、→CN' = →CN + →dCU+ →dCVとなる。
つまり、先ほどずっと計算していたUV平面と平行に移動する。
これでOBBの中央が求まった。
OBBの描画
OBBの中央が求まったら、そこから各方向の辺のベクトルの1/2を引けばOBBの端の点が求められる。
ソースコード
疲れたので次回。
Blender 雲(Volume)のチュートリアル抜粋
元は以下のチュートリアル:
なのだが無駄が多すぎる上に肝心な部分が瞬時に終わってしまうので抜粋する。なお同じ方向性でより優れたチュートリアルが複数あるので本来はそれを紹介したい。今回は手軽さを最優先にしている。
修正
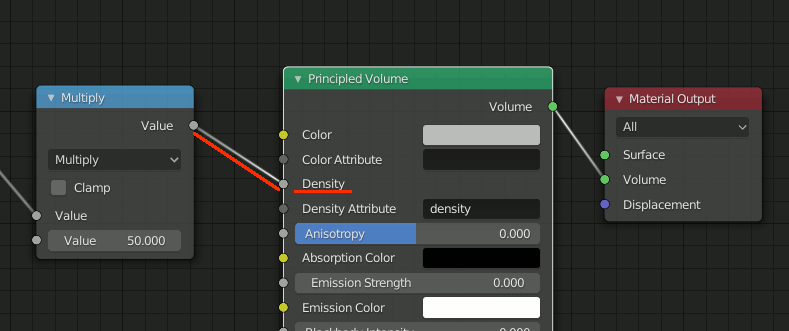
なお以降の画像中、Principled Volume側はDensityに接続する。
アップロードしてからミスに気づいたが修正する気力が無い。
手順
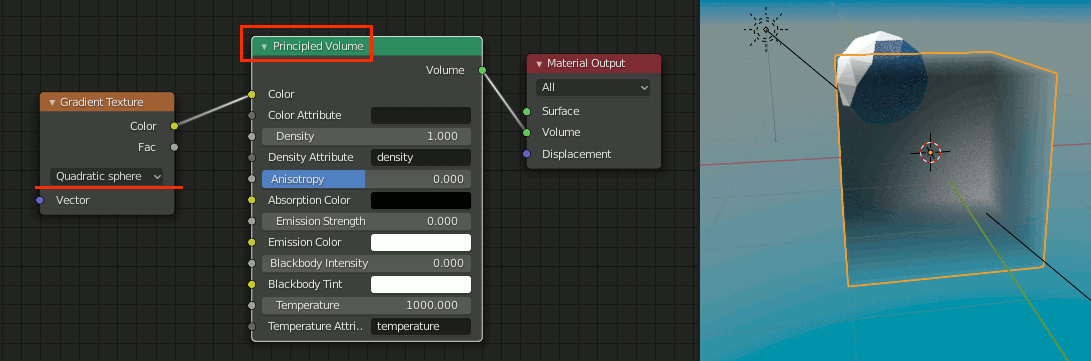
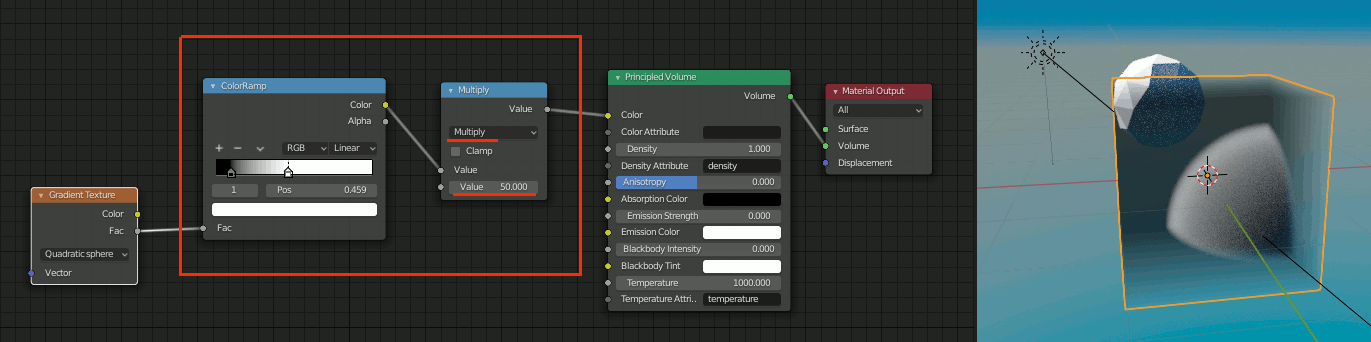
1.Principled Volume + Gradient Texture
[Shift+A]→[Texture]→[Gradient Texture]
[Shift+A]→[Shader]→Principled Volume
の二つを追加し、Gradient TextureをQuadratic sphereに設定
2. ColorRamp + Multiply
[Shift+A]→[Converter]→[ColorRamp]
[Shift+A]→[Converter]→[Math]
を追加し、MathをMultiplyに設定、ColorRampからの出力を50倍などの値に設定
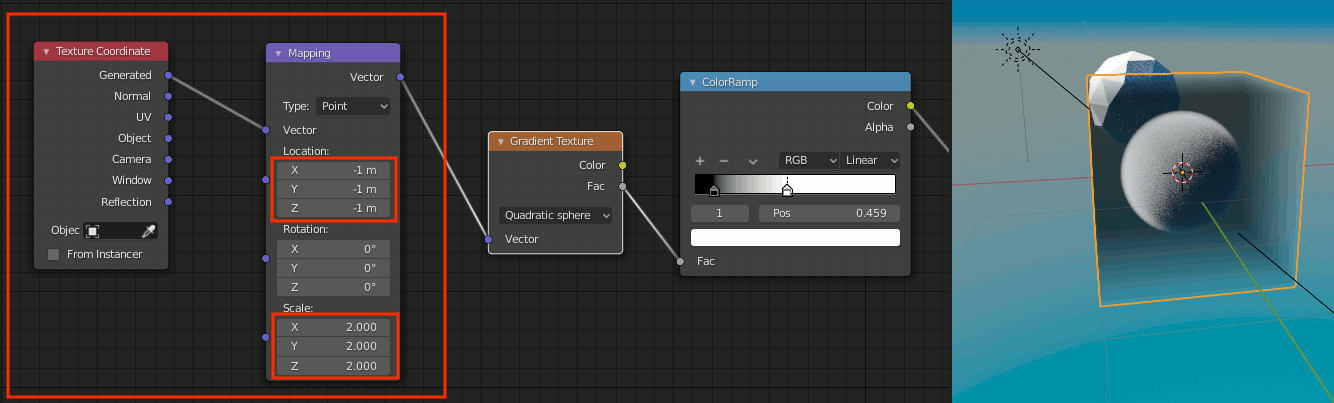
3. Texture Coordinate + Mapping追加
[Shift+A]→[input]→[Texture Coordinate]
[Shift+A]→[Vector]→[Mapping]
を追加し、MappingをLocationを(-1,-1,-1)、Scaleを(2,2,2)に設定する
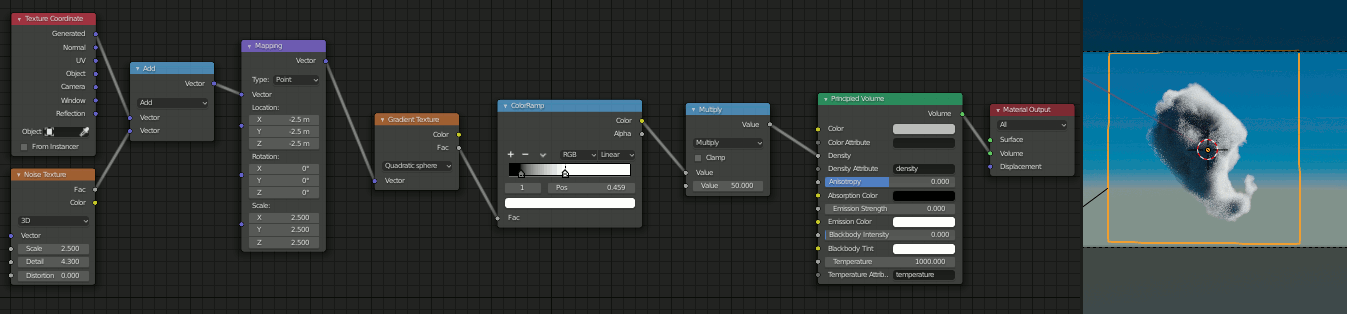
4. Noise Textureを加算
[Shift+A]→[Texture]→[Noise Texture]
[Shift+A]→[Converter]→[Vector Math]
をそれぞれ追加。
Texture CoordinateのGeneratedとNoise Textureを加算し、Mappingへ接続
Mapping側はLocationを(-2.5,-2.5,-2.5)、Scaleを(2.5,2.5,2.5)に変更
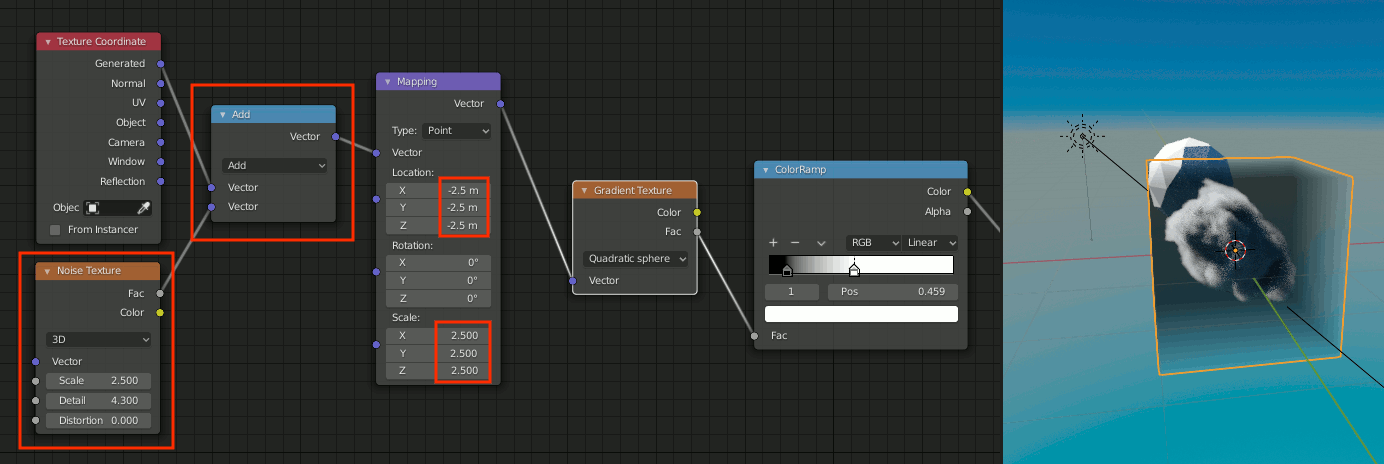
結果
BlenderでOSL
BlenderでOSLを使ってみる
作業の流れ
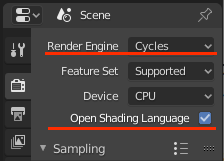
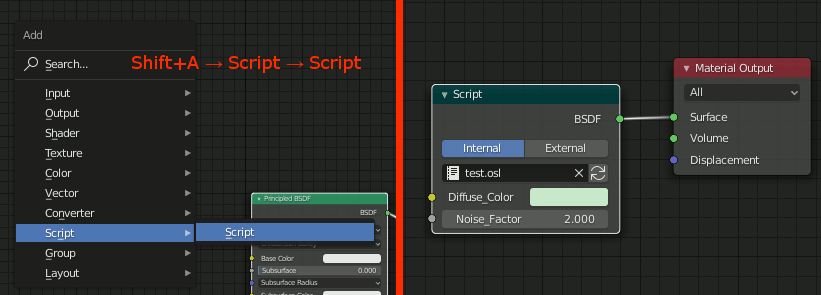
1.レンダラにCyclesを選択し、Open Shading Language にチェックを入れる
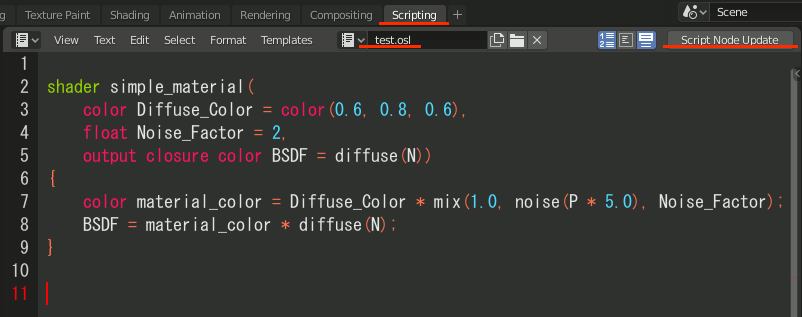
2.Scriptを書き、ファイル名を.oslの拡張子に変更、Script Node Updateをクリック
3.オブジェクトにマテリアルを設定、Shader EditorでScriptノードを追加、Material Outpuに連結
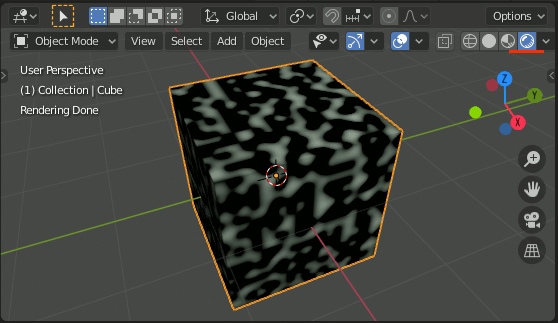
4.Viewport ShadingをRendered等にして結果を確認
詳細
1.レンダラにCyclesを選択し、Open Shading Language にチェックを入れる
2.Scriptを書き、ファイル名を.oslの拡張しに変更、Script Node Updateをクリック
プログラムは以下から。ただし結果がわかりやすいようにNoise_Factorの初期値とPの係数をわずかに変更している。
https://docs.blender.org/manual/ja/2.79/render/cycles/nodes/osl.html
3.オブジェクトにマテリアルを設定、Shader EditorでScriptノードを追加、Material Outpuに連結
4.Viewport ShadingをRendered等にして結果を確認
リンク
こちらのブログがものすごく重要な情報を纏めてくださっております。
公式のマニュアル
http://staffwww.itn.liu.se/~stegu/TNM084-2018/osl-languagespec.pdf
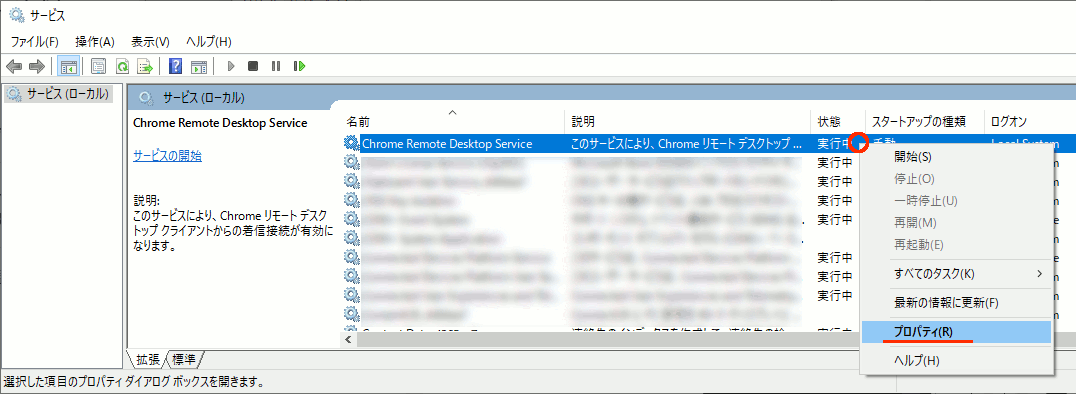
Googleリモートデスクトップのchromotingを停止
Windows 10でGoogleリモートデスクトップのサーバーなるとき、chromotingというサービスがインストールされ、常時起動するようになる。
調べた限りこいつが重大なセキュリティホールになるという話は見つからない。むしろ何らかの原因で停止したために接続できなくなった場合に起動方法を知っておこうという文脈の方が多い。
ただ個人的に、用途が明確にわかっていてかつ使わない遠隔操作用のサービスが動いているというのは気持ちが悪いので停止方法を調べた。
手順
①タスクバーを右クリック→タスクマネージャ
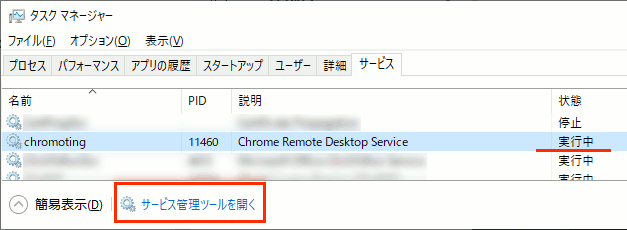
② "サービス" タグ → chromoting を見つけ、「実行中」になっている事を確認し、画面左下から、"サービス管理ツールを開く"
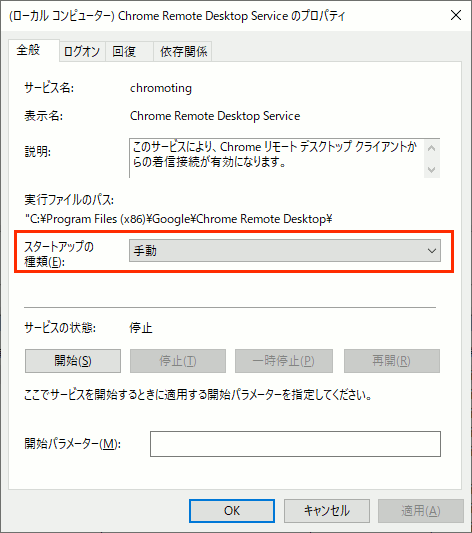
③ "Chrome Remote Desktop Service" を見つけ、右クリック → プロパティ
④ スタートアップの種類を「手動」または「無効」に設定
手動と無効の違い
・「手動」・・・サービスが必要になったときに勝手に実行され、サービスが不要になったときに勝手に停止する
・「停止」・・・ユーザが意図的に実行を指示しない限り動かない
手動だとサービスによっては停止したつもりでも殆ど起動しっぱなしという可能性もある。chromotingは見たところChromeを起動してChromeリモートデスクトップを使用中しか動かないように見えるが、不安なら「停止」にする。その代わり朝の忙しい時にリモートデスクトップの設定をする際に、chromotingの起動の手間が増える。
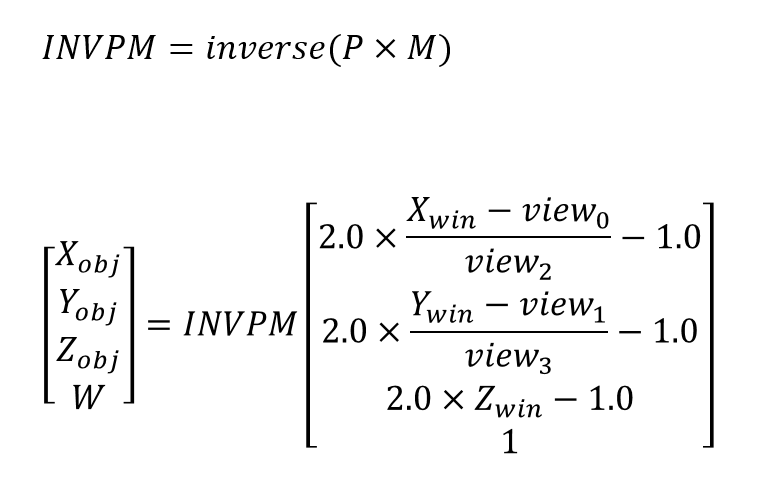
gluUnProjectを自前実装する
逆行列や行列の積に関しては以前の記事参照:
gluUnProjectもkhronosが言っている通りの式では結果が違ってしまうので実装例を確認してそちらに合わせた。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml
template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix44(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 4); } template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix_vec41(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 1); }
/////////////////////////////////////// // gluUnProject // https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml //! @brief gluUnProjectの自前実装版 //! @param [in] winX 画面上のX座標 //! @param [in] winY 画面上のY座標 //! @param [in] winZ 画面上のZ座標 //! @param [in] model モデルビュー行列 //! @param [in] proj プロジェクション行列 //! @param [in] ビューポート x,y,width,height //! @param [out] objX 空間座標のX //! @param [out] objY 空間座標のY //! @param [out] objZ 空間座標のZ //! @retval true 計算成功 //! @retval false 計算失敗
template<typename real_t> bool myUnProject( real_t winX, real_t winY, real_t winZ, const real_t* model, const real_t* proj, const int* view, real_t* objX, real_t* objY, real_t* objZ ) { real_t pm[16]; real_t invpm[16]; mult_matrix44(pm, proj, model);//pm = P×M bool ret = inverse_matrix44(invpm, pm);// pmの逆行列 if (ret == false) return false; real_t v[4] = { 2 * (winX - view[0]) / view[2] - 1.0 , 2 * (winY - view[1]) / view[3] - 1.0 , 2 * winZ - 1.0, 1 }; real_t vd[4]; mult_matrix_vec41(vd, invpm, v); // vd = invpm × v *objX = vd[0] / vd[3]; *objY = vd[1] / vd[3]; *objZ = vd[2] / vd[3]; return true; }
動作検証
int WIDTH = 300; int HEIGHT = 400; void disp(void) { glViewport(0, 0, WIDTH, HEIGHT); glMatrixMode(GL_PROJECTION); glPushMatrix(); glLoadIdentity(); gluPerspective(45, 0.5, 0.1, 2.5); glMatrixMode(GL_MODELVIEW); glPushMatrix(); glLoadIdentity(); glTranslated(-1, 0, -2); glRotated(1.5, 1.0, 1.0, 1.0);
////作成した変換行列を取得する GLdouble modeld[16]; glGetDoublev(GL_MODELVIEW_MATRIX, modeld); GLdouble projd[16]; glGetDoublev(GL_PROJECTION_MATRIX, projd); GLint view[4]; glGetIntegerv(GL_VIEWPORT, view);
// 三次元座標(出力) double objx, objy, objz; // 二次元ピクセル座標(入力) double winx = (rand() % 1000) / 100.0, winy = (rand() % 1000) / 100.0, winz = (rand() % 1000) / 100.0;
gluUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz); printf("glu %lf %lf %lf\n", objx, objy, objz);
myUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz ); printf("my %lf %lf %lf\n", objx, objy, objz);
puts("-----------"); glMatrixMode(GL_PROJECTION); glPopMatrix(); glMatrixMode(GL_MODELVIEW); glPopMatrix(); }
glu -1.165678 0.640021 1.701902 my -1.165678 0.640021 1.701902 ----------- glu -0.973079 0.946809 1.542299 my -0.973079 0.946809 1.542299 ----------- glu -0.734826 1.333922 1.296449 my -0.734826 1.333922 1.296449 ----------- glu -1.907228 1.907111 0.176182 my -1.907228 1.907111 0.176182 ----------- glu -1.917435 0.198937 1.894649 my -1.917435 0.198937 1.894649 ----------- glu -1.973992 0.975493 1.354121 my -1.973992 0.975493 1.354121 ----------- glu -1.364160 1.002119 1.417683 my -1.364160 1.002119 1.417683 ----------- glu -0.614162 0.527975 1.841761 my -0.614162 0.527975 1.841761 ----------- glu -0.323812 0.312351 1.947271 my -0.323812 0.312351 1.947271 -----------
gluProjectionを自前実装する
行列の積を自前実装できたのでgluProjectionを自前実装する。
数式
公式の式をそのまま使うとなぜか公式の結果と一致しない。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluProject.xml
実装例を見てみるとどうも式が若干違うのでそっちに合わせる。
http://collagefactory.blogspot.com/2010/03/gluproject-source-code.html
コード
//誤差の定義 template<typename T>struct real_error; template<>struct real_error<double> { static constexpr double value = 1e-15; }; template<>struct real_error<float> { static constexpr float value = (float)1e-7; }; //! @brief 誤差の閾値未満かをチェック //! @param [in] value 検査する値 //! @retval true 値の絶対値は閾値より小さい //! @retval false 値の絶対値は閾値より大きい template<typename T> inline bool is_error(const T value) { return abs(value) < real_error<T>::value; } //! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; } //! @brief IxJ行列 × JxK行列 の乗算関数 //https://suzulang.com/cpp-multmatrix44/ //! @param [out] C Cik 計算結果格納先 //! @param [in] A Aijの行列 //! @param [in] B Bjkの行列 //! @param [in] I Aの行列の行数 //! @param [in] J Aの行列の列数 //! @param [in] K Bの行列の列数 //! @return C template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrixIJK(real_tC* C, const real_tA* A, const real_tB* B, const int I, const int J, const int K) { for (int i = 0; i < I; i++) for (int k = 0; k < K; k++) { C[matijI(i, k, I)] = 0.0; for (int j = 0; j < J; j++) { C[matijI(i, k, I)] += A[matijI(i, j, I)] * B[matijI(j, k, J)]; } } return C; } template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix_vec41(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 1); }
// gluProject // https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluProject.xml // http://collagefactory.blogspot.com/2010/03/gluproject-source-code.html
//! @brief gluProjectの自前実装版 //! @param [in] wldX 空間座標のX //! @param [in] wldY 空間座標のY //! @param [in] wldZ 空間座標のZ //! @param [in] model モデルビュー行列 //! @param [in] proj プロジェクション行列 //! @param [in] ビューポート x,y,width,height //! @param [out] pixX 画面上のX座標 //! @param [out] pixY 画面上のY座標 //! @param [out] pixZ 画面上のZ座標 ※計算上は存在する //! @retval true 計算に成功 //! @retval false 計算に失敗 template<typename real_t> inline bool myProject( real_t wldX, real_t wldY, real_t wldZ, const real_t* model, const real_t* proj, const int* view, real_t* pixX, real_t* pixY, real_t* pixZ ) { real_t world[4] = { wldX,wldY,wldZ,1.0 }; real_t tmp[4]; real_t vdd[4]; mult_matrix_vec41(tmp, model, world); // tmp = M×v mult_matrix_vec41( vdd, proj, tmp ); // v'' = P×tmp if (is_error(vdd[3]) == true) return false; vdd[0] /= vdd[3]; vdd[1] /= vdd[3]; vdd[2] /= vdd[3]; //v''' = v'' / v''[3] *pixX = view[0] + view[2] * (vdd[0] + 1) / 2.0; *pixY = view[1] + view[3] * (vdd[1] + 1) / 2.0; *pixZ = (vdd[2] + 1) / 2.0; return true; }
動作チェック
gluProjectionと同じパラメータを入力し同じ結果が出るかを確認する。
テストコード
int WIDTH = 300; int HEIGHT = 400; void disp(void) { glViewport(0, 0, WIDTH, HEIGHT); glMatrixMode(GL_PROJECTION);
glPushMatrix();
glLoadIdentity(); gluPerspective(45, 0.5, 0.1, 2.5); glMatrixMode(GL_MODELVIEW); glPushMatrix();
glLoadIdentity();
glTranslated(-1, 0, -2); glRotated(1.5, 1.0, 1.0, 1.0);
////作成した変換行列を取得する GLdouble modeld[16]; glGetDoublev(GL_MODELVIEW_MATRIX, modeld); GLdouble projd[16]; glGetDoublev(GL_PROJECTION_MATRIX, projd); GLint view[4]; glGetIntegerv(GL_VIEWPORT, view);
// 三次元座標(入力) double objx = (rand() % 1000) / 1000.0, objy = (rand() % 1000) / 1000.0, objz = (rand() % 1000) / 1000.0; // 二次元ピクセル座標(出力) double winx, winy, winz;
gluProject( objx, objy, objz, modeld, projd, view, &winx, &winy, &winz); printf("glu %lf %lf %lf\n", winx, winy, winz);
myProject(objx, objy, objz, modeld, projd, view, &winx, &winy, &winz); printf("my %lf %lf %lf\n", winx, winy, winz);
puts("-----------"); glMatrixMode(GL_PROJECTION); glPopMatrix(); glMatrixMode(GL_MODELVIEW); glPopMatrix(); }
実行結果
glu -269.362487 334.563333 0.978900
my -269.362487 334.563333 0.978900
-----------
glu -127.939462 262.458218 0.960356
my -127.939462 262.458218 0.960356
-----------
glu -207.160157 362.861399 0.941500
my -207.160157 362.861399 0.941500
-----------
glu -63.012933 385.110848 0.985399
my -63.012933 385.110848 0.985399
-----------
glu -353.644733 582.528452 0.940617
my -353.644733 582.528452 0.940617
-----------
glu -201.429535 654.202066 0.942501
my -201.429535 654.202066 0.942501
-----------
glu 72.061917 332.346399 0.977161
my 72.061917 332.346399 0.977161
-----------
glu -10.131515 438.149822 0.985127
my -10.131515 438.149822 0.985127
-----------
C++でI×J行列 × J×K行列
4x4行列の積を求めるプログラムをほんの少し改良しただけなのだが、C++でIxJ行列とJxK行列の積を求めるプログラムを書く。与える行列の表現は一次元配列で、OpenGLと同じ表現方法。
コード
//! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; } //! @brief IxJ行列 × JxK行列 の積 //! @param [out] C Cik 計算結果格納先 //! @param [in] A Aijの行列 //! @param [in] B Bjkの行列 //! @param [in] I Aの行列の行数 //! @param [in] J Aの行列の列数 //! @param [in] K Bの行列の列数 //! @return C template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrixIJK(real_tC* C, const real_tA* A, const real_tB* B, const int I, const int J, const int K) { for (int i = 0; i < I; i++) for (int k = 0; k < K; k++) { C[matijI(i, k, I)] = 0.0; for (int j = 0; j < J; j++) { C[matijI(i, k, I)] += A[matijI(i, j, I)] * B[matijI(j, k, J)]; } } return C; }
動作検証
Eigenとの結果比較
#include <Eigen/Dense>
void mult_matrix_check() {
std::cout << "---------- Eigen ------------" << std::endl; Eigen::MatrixXf mat53(5,3); mat53(0, 0) = 00; mat53(0, 1) = 01; mat53(0, 2) = 02; mat53(1, 0) = 10; mat53(1, 1) = 11; mat53(1, 2) = 12; mat53(2, 0) = 20; mat53(2, 1) = 21; mat53(2, 2) = 22; mat53(3, 0) = 30; mat53(3, 1) = 31; mat53(3, 2) = 32; mat53(4, 0) = 40; mat53(4, 1) = 41; mat53(4, 2) = 42; Eigen::MatrixXf mat34(3, 4); mat34(0, 0) = 100; mat34(0, 1) = 101; mat34(0, 2) = 102; mat34(0, 3) = 103; mat34(1, 0) = 110; mat34(1, 1) = 111; mat34(1, 2) = 112; mat34(1, 3) = 113; mat34(2, 0) = 120; mat34(2, 1) = 121; mat34(2, 2) = 122; mat34(2, 3) = 123; std::cout << "---------- Eigen mat 1" << std::endl; std::cout << mat53 << std::endl; std::cout << "---------- Eigen mat 2" << std::endl; std::cout << mat34 << std::endl; std::cout << "---------- Eigen mat1*mat2" << std::endl; std::cout << mat53 * mat34 << std::endl;
std::cout << "---------- 自前実装 ------------" << std::endl; int I; float fmat53[5 * 3]; I = 5; fmat53[matijI(0, 0, I)] = 00; fmat53[matijI(0, 1, I)] = 01; fmat53[matijI(0, 2, I)] = 02; fmat53[matijI(1, 0, I)] = 10; fmat53[matijI(1, 1, I)] = 11; fmat53[matijI(1, 2, I)] = 12; fmat53[matijI(2, 0, I)] = 20; fmat53[matijI(2, 1, I)] = 21; fmat53[matijI(2, 2, I)] = 22; fmat53[matijI(3, 0, I)] = 30; fmat53[matijI(3, 1, I)] = 31; fmat53[matijI(3, 2, I)] = 32; fmat53[matijI(4, 0, I)] = 40; fmat53[matijI(4, 1, I)] = 41; fmat53[matijI(4, 2, I)] = 42; float fmat34[3 * 4]; I = 3; fmat34[matijI(0, 0, I)] = 100; fmat34[matijI(0, 1, I)] = 101; fmat34[matijI(0, 2, I)] = 102; fmat34[matijI(0, 3, I)] = 103; fmat34[matijI(1, 0, I)] = 110; fmat34[matijI(1, 1, I)] = 111; fmat34[matijI(1, 2, I)] = 112; fmat34[matijI(1, 3, I)] = 113; fmat34[matijI(2, 0, I)] = 120; fmat34[matijI(2, 1, I)] = 121; fmat34[matijI(2, 2, I)] = 122; fmat34[matijI(2, 3, I)] = 123; std::cout << "---------- 自前実装 mat 1" << std::endl; std::cout << mat_to_string(fmat53, "%3.0lf", 5, 3); std::cout << "---------- 自前実装 mat 2" << std::endl; std::cout << mat_to_string(fmat34, "%3.0lf", 3, 4); std::cout << "---------- 自前実装 mat1*mat2" << std::endl; float fmat54[5 * 4]; mult_matrixIJK(fmat54, fmat53, fmat34, 5, 3, 4); std::cout << mat_to_string(fmat54, "%5.0lf", 5, 4);
}
出力結果
---------- Eigen ------------ ---------- Eigen mat 1 0 1 2 10 11 12 20 21 22 30 31 32 40 41 42 ---------- Eigen mat 2 100 101 102 103 110 111 112 113 120 121 122 123 ---------- Eigen mat1*mat2 350 353 356 359 3650 3683 3716 3749 6950 7013 7076 7139 10250 10343 10436 10529 13550 13673 13796 13919
---------- 自前実装 ------------ ---------- 自前実装 mat 1 0 1 2 10 11 12 20 21 22 30 31 32 40 41 42 ---------- 自前実装 mat 2 100 101 102 103 110 111 112 113 120 121 122 123 ---------- 自前実装 mat1*mat2 350 353 356 359 3650 3683 3716 3749 6950 7013 7076 7139 10250 10343 10436 10529 13550 13673 13796 13919
OpenGLの行列の表記とC/C++での扱い
やっていると時々混乱し、致命的なミスを犯すので確認しておきたい。
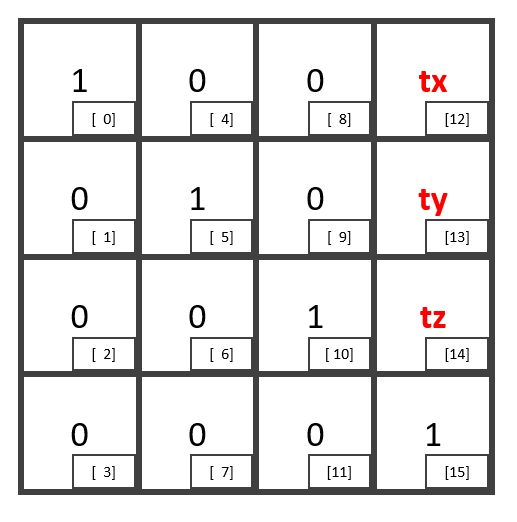
まず、以下はOpenGLの移動行列。一番右側の列に移動パラメータが入る。
そしてこれは揺るがない。数学の世界、概念の世界の話なので。
次に、C/C++でこれがどう表現されているのか。以下のプログラムで確認する。
//OpenGLの機能で変換行列を作成する
glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2);
//作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf);
//取得した変換行列を表示する for (int i = 0; i < 16; i++) { printf("[%2d] = %3.0lf\n",i, modelf[i]); }
結果
[ 1] = 0
[ 2] = 0
[ 3] = 0
[ 4] = 0
[ 5] = 1
[ 6] = 0
[ 7] = 0
[ 8] = 0
[ 9] = 0
[10] = 1
[11] = 0
[12] = -1
[13] = 0
[14] = -2
[15] = 1
これをそのまま4要素区切りで表示すると、以下のように転置でもしたかのように見えてしまう。これはバグでも何でも無く、「現実世界の実物がプログラム中でどう表現されているか」という問題でしかない。
//OpenGLの機能で変換行列を作成する glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2); //作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf); //取得した変換行列を表示する for (int i = 0; i < 16; i++) { if (i % 4 == 0) puts(""); printf("%3.0lf", modelf[i]); }
結果
1 0 0 0 0 1 0 0 0 0 1 0 -1 0 -2 1
そして、OpenGLでは”行列”を、配列を用いて以下の形で表現している。
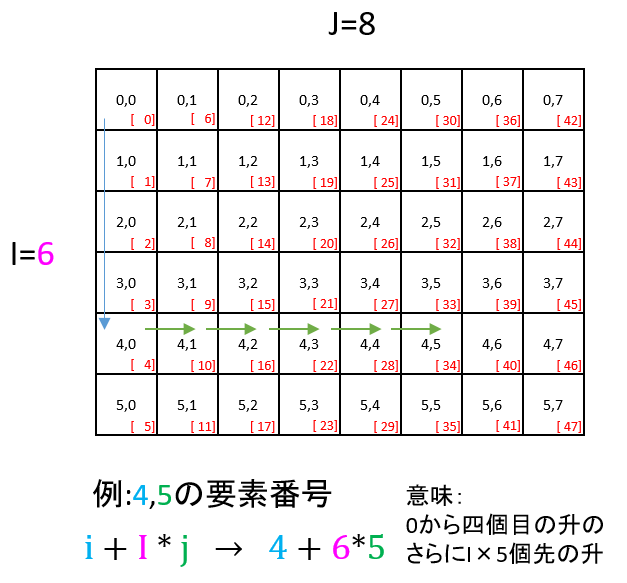
この配列に対して、数学的にアクセスしたい場合、以下のような計算で要素番号を求める。
//! @brief 4x4行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 inline int matij4(const int i, const int j) { return i + 4 * j; }
より一般的なアクセス
OpenGLの行列は4x4や3x3だけ考えればいいが、より一般的な行列演算関数の中でi,jから行列の添え字に変換するにはどうすればいいか。以下のような計算を行う。
//! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; }
この考え方ではまず行を調整し、現在位置から一列の要素数×列番号だけ移動する。(※一列の要素数==行数、一行の要素数==列数)
OpenGL形式の表現の行列を表示する関数
関数本体
//! @brief 指定した行列を表示する関数
//! @param [in] m 行列を表す一次元配列
//! @param [in] format printf形式の書式
//! @param [in] I 行数
//! @param [in] J 列数
template<typename real_t> inline std::string mat_to_string(const real_t* m, const char* format,int I,int J) { std::stringstream s; char tmp[100]; for (int i = 0; i < I; i++) { for (int j = 0; j < J; j++) { sprintf(tmp, format, m[matijI(i, j,I)] ); s << tmp << " "; } s << "\n"; } return s.str(); }
使用例
//OpenGLの機能で変換行列を作成する glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2); //作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf); std::cout << mat_to_string(modelf, "%02.3f", 4, 4);
結果
数学的に表示できていることを確認する。
1.000 0.000 0.000 -1.000 0.000 1.000 0.000 0.000 0.000 0.000 1.000 -2.000 0.000 0.000 0.000 1.000
4×4の逆行列を求める関数
3DCGには欠かせない4×4行列の逆行列を求める関数を自前実装する。
動作チェックはEigenとの差を見て判断する。
逆行列を求める関数
namespace matcalc {
//誤差の定義 template<typename T> struct real_error {static constexpr float value = (float)1e-7;}; template<> struct real_error<double> { static constexpr double value = 1e-15; }; //! @brief 誤差の閾値未満かをチェック //! @param [in] value 検査する値 //! @retval true 値の絶対値は閾値より小さい //! @retval false 値の絶対値は閾値より大きい template<typename T> inline bool is_error(const T value) { return abs(value) < real_error<T>::value; }
//! @brief 4x4行列の行列式を取得 //! @param [in] dm16 4x4行列 //! @return 行列式 template<typename real_t> inline auto determinant44(const real_t* dm16) { using scalar_t = decltype(dm16[0]); const scalar_t a11 = dm16[0]; const scalar_t a12 = dm16[1]; const scalar_t a13 = dm16[2]; const scalar_t a14 = dm16[3]; const scalar_t a21 = dm16[4]; const scalar_t a22 = dm16[5]; const scalar_t a23 = dm16[6]; const scalar_t a24 = dm16[7]; const scalar_t a31 = dm16[8]; const scalar_t a32 = dm16[9]; const scalar_t a33 = dm16[10]; const scalar_t a34 = dm16[11]; const scalar_t a41 = dm16[12]; const scalar_t a42 = dm16[13]; const scalar_t a43 = dm16[14]; const scalar_t a44 = dm16[15]; return a11 * a22* a33* a44 + a11 * a23 * a34 * a42 + a11 * a24 * a32 * a43 + a12 * a21 * a34 * a43 + a12 * a23 * a31 * a44 + a12 * a24 * a33 * a41 + a13 * a21 * a32 * a44 + a13 * a22 * a34 * a41 + a13 * a24 * a31 * a42 + a14 * a21 * a33 * a42 + a14 * a22 * a31 * a43 + a14 * a23 * a32 * a41 - a11 * a22 * a34 * a43 - a11 * a23 * a32 * a44 - a11 * a24 * a33 * a42 - a12 * a21 * a33 * a44 - a12 * a23 * a34 * a41 - a12 * a24 * a31 * a43 - a13 * a21 * a34 * a42 - a13 * a22 * a31 * a44 - a13 * a24 * a32 * a41 - a14 * a21 * a32 * a43 - a14 * a22 * a33 * a41 - a14 * a23 * a31 * a42; }
//! @brief 4x4行列の逆行列を取得 //! @param [out] dst_dm16 結果を格納する一次元配列 //! @param [in] src_dm16 元の行列 //! @retval true 成功した //! @retval false 行列式の大きさが小さすぎて失敗した template<typename real_t> inline bool inverse_matrix44(real_t* dst_dm16, const real_t* src_dm16) { using s_scalar_t = decltype(src_dm16[0]); using d_scalar_t = decltype(dst_dm16[0]); real_t a11 = src_dm16[0]; real_t a12 = src_dm16[1]; real_t a13 = src_dm16[2]; real_t a14 = src_dm16[3]; real_t a21 = src_dm16[4]; real_t a22 = src_dm16[5]; real_t a23 = src_dm16[6]; real_t a24 = src_dm16[7]; real_t a31 = src_dm16[8]; real_t a32 = src_dm16[9]; real_t a33 = src_dm16[10]; real_t a34 = src_dm16[11]; real_t a41 = src_dm16[12]; real_t a42 = src_dm16[13]; real_t a43 = src_dm16[14]; real_t a44 = src_dm16[15]; real_t& b11 = dst_dm16[0]; real_t& b12 = dst_dm16[1]; real_t& b13 = dst_dm16[2]; real_t& b14 = dst_dm16[3]; real_t& b21 = dst_dm16[4]; real_t& b22 = dst_dm16[5]; real_t& b23 = dst_dm16[6]; real_t& b24 = dst_dm16[7]; real_t& b31 = dst_dm16[8]; real_t& b32 = dst_dm16[9]; real_t& b33 = dst_dm16[10]; real_t& b34 = dst_dm16[11]; real_t& b41 = dst_dm16[12]; real_t& b42 = dst_dm16[13]; real_t& b43 = dst_dm16[14]; real_t& b44 = dst_dm16[15]; b11 = a22 * a33 * a44 + a23 * a34 * a42 + a24 * a32 * a43 - a22 * a34 * a43 - a23 * a32 * a44 - a24 * a33 * a42; b12 = a12 * a34 * a43 + a13 * a32 * a44 + a14 * a33 * a42 - a12 * a33 * a44 - a13 * a34 * a42 - a14 * a32 * a43; b13 = a12 * a23 * a44 + a13 * a24 * a42 + a14 * a22 * a43 - a12 * a24 * a43 - a13 * a22 * a44 - a14 * a23 * a42; b14 = a12 * a24 * a33 + a13 * a22 * a34 + a14 * a23 * a32 - a12 * a23 * a34 - a13 * a24 * a32 - a14 * a22 * a33; b21 = a21 * a34 * a43 + a23 * a31 * a44 + a24 * a33 * a41 - a21 * a33 * a44 - a23 * a34 * a41 - a24 * a31 * a43; b22 = a11 * a33 * a44 + a13 * a34 * a41 + a14 * a31 * a43 - a11 * a34 * a43 - a13 * a31 * a44 - a14 * a33 * a41; b23 = a11 * a24 * a43 + a13 * a21 * a44 + a14 * a23 * a41 - a11 * a23 * a44 - a13 * a24 * a41 - a14 * a21 * a43; b24 = a11 * a23 * a34 + a13 * a24 * a31 + a14 * a21 * a33 - a11 * a24 * a33 - a13 * a21 * a34 - a14 * a23 * a31; b31 = a21 * a32 * a44 + a22 * a34 * a41 + a24 * a31 * a42 - a21 * a34 * a42 - a22 * a31 * a44 - a24 * a32 * a41; b32 = a11 * a34 * a42 + a12 * a31 * a44 + a14 * a32 * a41 - a11 * a32 * a44 - a12 * a34 * a41 - a14 * a31 * a42; b33 = a11 * a22 * a44 + a12 * a24 * a41 + a14 * a21 * a42 - a11 * a24 * a42 - a12 * a21 * a44 - a14 * a22 * a41; b34 = a11 * a24 * a32 + a12 * a21 * a34 + a14 * a22 * a31 - a11 * a22 * a34 - a12 * a24 * a31 - a14 * a21 * a32; b41 = a21 * a33 * a42 + a22 * a31 * a43 + a23 * a32 * a41 - a21 * a32 * a43 - a22 * a33 * a41 - a23 * a31 * a42; b42 = a11 * a32 * a43 + a12 * a33 * a41 + a13 * a31 * a42 - a11 * a33 * a42 - a12 * a31 * a43 - a13 * a32 * a41; b43 = a11 * a23 * a42 + a12 * a21 * a43 + a13 * a22 * a41 - a11 * a22 * a43 - a12 * a23 * a41 - a13 * a21 * a42; b44 = a11 * a22 * a33 + a12 * a23 * a31 + a13 * a21 * a32 - a11 * a23 * a32 - a12 * a21 * a33 - a13 * a22 * a31; auto detA = determinant44(src_dm16); if (is_error(detA) == true) return false; detA = static_cast<decltype(detA)>(1.0) / detA; for (int i = 0; i < 16; i++) { dst_dm16[i] *= detA; } return true; }
}
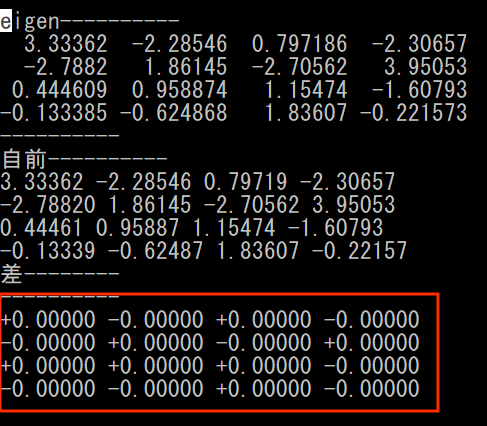
動作チェック
#include<Eigen/Dense> #include "inversematrix.hpp" //自前実装版 void inversematrix_check() { ///////////////////////////////////////////// // 元データ double base[16]; for (size_t i = 0; i < 16; i++) { base[i] = rand() % 1000 / 1000.0; }
///////////////////////////////////////////// // Eigenで求める Eigen::MatrixXd eg(4, 4); eg << base[0], base[1], base[2], base[3], base[4], base[5], base[6], base[7], base[8], base[9], base[10], base[11], base[12], base[13], base[14], base[15]; auto inv = eg.inverse(); std::cout << "eigen----------" << std::endl; std::cout << inv << std::endl; std::cout << "----------" << std::endl;
///////////////////////////////////////////// //自前実装版 double* A = new double[4 * 4]{ base[0], base[1], base[2], base[3] , base[4], base[5], base[6], base[7] , base[8], base[9], base[10], base[11] , base[12], base[13], base[14], base[15] }; double* B = new double[4 * 4]; matcalc::inverse_matrix44(B, A); #pragma warning(push) #pragma warning(disable:4996) std::cout << "自前----------" << std::endl; for (int i = 0; i < 4; i++) { for (int j = 0; j < 4; j++) { printf("%0.5lf", B[i*4+ j]); printf(" "); } puts(""); }
std::cout << "差--------" << std::endl; std::cout << "----------" << std::endl; for (int i = 0; i < 4; i++) { for (int j = 0; j < 4; j++) { printf("%+0.5lf", B[i * 4 + j]-inv(i,j)); printf(" "); } puts(""); }
std::cout << std::endl << std::endl << std::endl; #pragma warning(pop) }
テスト結果
DIBの4バイト境界について。あとDIBの保存。
BMPファイルは1スキャンラインを4バイト境界に合わせなければならないという所を前回確認した。
実はDIB Sectionでアクセスできる画素データは、この4バイト境界が考慮されている。つまり24ビットDIBで幅が4バイトの倍数にない場合、画像内に4バイト境界に合わせるためのダミーデータが点在している。
これはこれでいいのだが、画素データを直接編集したいだけの場合は注意が必要で、普通に画像幅×y座標+x座標の式で目的の画素のアドレスを求められないことになる。といっても画素幅が画素バイトになるだけなのだが。
4の倍数ということは素因数分解したときに2が二つ以上出てくるということで、この条件を満たす数はかなり多い。例えば100は2^2×5^2なので、100の倍数は全て4バイト境界の条件を満たす。だから実験として300x300とかの画像で確認などすると正常に動作してしまい、考慮漏れとなる可能性がある。言うまでもないことだが256や512など2のn乗系の数字は0,1,2以外全部当てはまる。
実験コード
このプログラムでは24bit DIBを作り画面に表示して保存している。画素のアドレスはCalcPosで行っているが、移動方法は
としている。
なお1スキャンラインバイト数の計算とBMPファイルへの書き出しは前回作成したBMPwriter.hppの関数を使っている。
#include<windows.h> #include "BMPwriter.hpp"
BITMAPINFO bmpInfo; //!< CreateDIBSectionに渡す構造体 LPDWORD lpPixel; //!< 画素へのポインタ HBITMAP hBitmap; //!< 作成したMDCのビットマップハンドル HDC hMemDC; //!< 作成したMDCのハンドル //24bit DIB 作成 void createMemDC_24(HDC hdc,int width,int height) { //DIBの情報を設定する bmpInfo.bmiHeader.biSize = sizeof(BITMAPINFOHEADER); bmpInfo.bmiHeader.biWidth = width; bmpInfo.bmiHeader.biHeight = -height; //-を指定しないと上下逆になる bmpInfo.bmiHeader.biPlanes = 1; bmpInfo.bmiHeader.biBitCount = 24; bmpInfo.bmiHeader.biCompression = BI_RGB; hBitmap = CreateDIBSection(hdc, &bmpInfo, DIB_RGB_COLORS, (void**)& lpPixel, nullptr, 0); hMemDC = CreateCompatibleDC(hdc); SelectObject(hMemDC, hBitmap); }
//1スキャンラインのバイト数(何バイト移動すれば次の行へいけるのか)を計算 int get_scanline_bytes(const int width,const int bitcount) { return width * (bitcount / 8) + getbmp4line_err(width, bitcount); //getbmp4line_errはBMPwriter.hpp内 } //! @brief 与えられた座標のアドレスを返す //! @param [in] head 画像の先頭アドレス //! @param [in] width 画像幅(画素数) //! @param [in] height 画像高さ(画素数) //! @param [in] x x座標 //! @param [in] y y座標 //! @param [in] bitcount 1画素のビット数 //! @return x,yの要素のアドレス unsigned char* calcPos( unsigned char* head, int width, int height, int x, int y, int bitcount) { int pixelbyte = bitcount / 8; int scanlinebyte = get_scanline_bytes(width, bitcount); unsigned char* yhead = head + scanlinebyte * y; return yhead + x * pixelbyte; }
//! @brief 画像を灰色で塗りつぶす //! @param [in] 対象となる画像の先頭アドレス //! @param [in] width 画像幅(画素数) //! @param [in] height 画像高さ(画素数) //! @param [in] bitcount DIBの1画素のビット数 //! @return なし void clear_data(unsigned char* img, int width, int height, int bitcount) { int scanlinebyte = get_scanline_bytes(width, bitcount); int size = scanlinebyte * height; for (size_t i = 0; i < size; i++) { img[i] = 200; } } //! @brief 画像の真ん中に線を引く //! @param [in] 対象となる画像の先頭アドレス //! @param [in] width 画像幅(画素数) //! @param [in] height 画像高さ(画素数) //! @param [in] bitcount DIBの1画素のビット数 //! @return なし void drawline_data(unsigned char* img, int width, int height,int bitcount) { for (int y = 0; y < height; y++) { for (int x = 0; x < width; x++) { unsigned char* pos = calcPos(img, width, height, x, y, bitcount); if (x == width / 2) { pos[0] = 255; pos[1] = 0; pos[2] = 0; } } } }
LRESULT CALLBACK WndProc(HWND hwnd, UINT msg, WPARAM wp, LPARAM lp) { PAINTSTRUCT ps; static HPEN hpen1; static HPEN hpen2; static HPEN open; int iwidth = 4*30+1; //4の倍数にならない値を作成 int iheight = 80; switch (msg) { case WM_CREATE: { HDC hdc = GetDC(hwnd); createMemDC_24(hdc, iwidth, iheight);//24bit DIB 作成 ReleaseDC(hwnd, hdc); //DIBを灰色でクリア clear_data((unsigned char*)lpPixel, iwidth, iheight, 24); hpen1 = CreatePen(PS_SOLID, 5, RGB(255, 0, 0));// 何かしら描画する hpen2 = CreatePen(PS_SOLID, 3, RGB(0, 0, 255)); open = (HPEN)SelectObject(hMemDC, hpen1); MoveToEx(hMemDC, 0, 0, nullptr); LineTo(hMemDC, 20, 50); SelectObject(hMemDC, hpen2); MoveToEx(hMemDC, 0, 0, nullptr); LineTo(hMemDC, 50, 20); SelectObject(hMemDC, open); drawline_data((unsigned char*)lpPixel, iwidth, iheight,24);//縦に一本線を入れる。座標計算が間違っていたら斜めの線になる
//bmpファイルに保存。lpPixelは4byte境界が考慮されているのでそのまま出力できる。bmp_writeはBMPwriter.hpp内 bmp_write(L"c:\\data\\a.bmp", lpPixel, iwidth, iheight, 24);
} return 0; case WM_PAINT: { HDC hdc = BeginPaint(hwnd, &ps); BitBlt(hdc, 0, 0, iwidth, iheight, hMemDC, 0, 0, SRCCOPY);// 画像を画面に表示 EndPaint(hwnd, &ps); } return 0; case WM_DESTROY: DeleteObject(hpen1); DeleteObject(hpen2); PostQuitMessage(0); return 0; } return DefWindowProc(hwnd, msg, wp, lp); }
//! @brief エントリポイント //! @param [in] hInstance 現在のインスタンスハンドル //! @param [in] hPrevInstance 以前のインスタンスハンドル //! @param [in] lpCmdLine コマンドライン引数の文字列 //! @param [in] ウィンドウの表示状態 int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, PSTR lpCmdLine, int nCmdShow) { WNDCLASSEX wc; wc.cbSize = sizeof(WNDCLASSEX); wc.style = CS_HREDRAW | CS_VREDRAW; wc.lpfnWndProc = WndProc; wc.cbClsExtra = 0; wc.cbWndExtra = 0; wc.hInstance = hInstance; wc.hIcon = LoadIcon(NULL, IDI_APPLICATION); wc.hCursor = LoadCursor(NULL, IDC_ARROW); wc.hbrBackground = (HBRUSH)GetStockObject(WHITE_BRUSH); wc.lpszMenuName = NULL; wc.lpszClassName = TEXT("SZLCODE"); wc.hIconSm = LoadIcon(NULL, IDI_APPLICATION); if (!RegisterClassEx(&wc)) return 0; const int top = CW_USEDEFAULT; const int left = CW_USEDEFAULT; const int width = 300; const int height = 200; HWND hwnd; hwnd = CreateWindowEx( WS_EX_COMPOSITED, TEXT("SZLCODE"), TEXT("win32api example"), WS_OVERLAPPEDWINDOW | WS_VISIBLE, top, left, width, height, NULL, NULL, hInstance, NULL ); if (hwnd == NULL) return 0; // MSG msg; while (GetMessage(&msg, NULL, 0, 0)) { TranslateMessage(&msg); DispatchMessage(&msg); } return (int)msg.wParam; }