月火水木金土日
VCG LibraryでkdTree
VCGで点群を検索するサンプルです。
0. vcg/space/index/kdtree/kdtree.h をinclude
#include <vcg/space/index/kdtree/kdtree.h>
1.点群を準備
auto itr = vcg::tri::Allocator<MyMesh>::AddVertices(mesh, 30000); for (size_t i = 0; i < 30000; i++) { double k1 = rand() / (double)RAND_MAX; double k2 = rand() / (double)RAND_MAX; double k3 = rand() / (double)RAND_MAX; itr[i].P() = vcg::Point3f(k1, k2, k3); itr[i].dist = 0.6; }
2. 検索結果を格納する配列を定義
// 検索して得られた頂点IDを格納する std::vector<unsigned int> vpid; // 検索して得られた頂点の、指定した座標からの距離を格納する std::vector<float> vpdst;
3.kdTreeで指定した座標付近の点群を取得
vcg::VertexConstDataWrapper<MyMesh> ww(mesh); vcg::KdTree<float> tree(ww); //検索する座標 p を定義 vcg::Point3f p(0.5, 0.5, 0.5); double distance = 0.5; //検索 tree.doQueryDist(p, distance, vpid, vpdst);
4. 取得した点群に対して処理
//検索して得られた頂点に、pとの二乗距離を格納(distメンバ変数は自分で定義したもの) for(int i = 0; i < vpid.size();i++){ mesh.vert[ vpid[i] ].dist = vpdst[i]; }
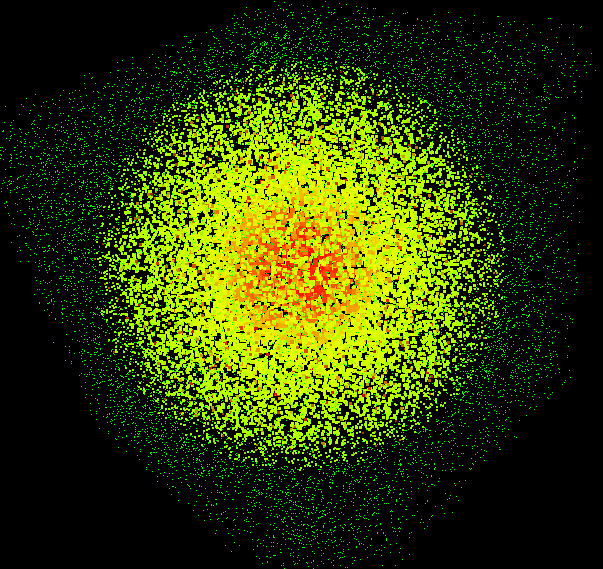
doQueryDist
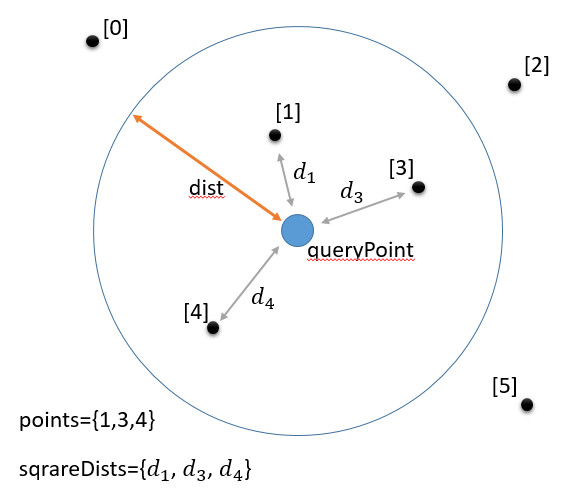
doQueryDist(
const VectorType& queryPoint,
float dist,
std::vector& points,
std::vector& sqrareDists
)
SquareDistance
距離計算に内部で使っているquaredNorm()関数の処理は、
/// Squared euclidian normal inline T SquaredNorm() const { return _v[0]*_v[0] + _v[1]*_v[1] + _v[2]*_v[2] + _v[3]*_v[3]; }
となっていますので、実際の距離を知りたい場合はsqrtする必要があります。
VCG LibraryのBall Pivotingでメッシュ生成
VCG Library ターゲットの周辺のオブジェクトを取得
VCG LibのFace-FaceやEdge-Faceなどの関連付け