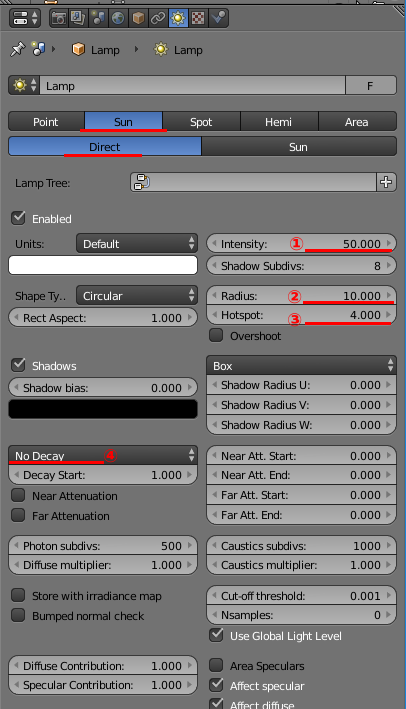
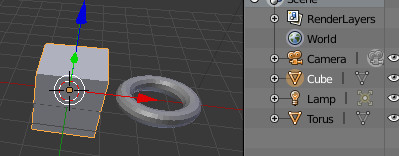
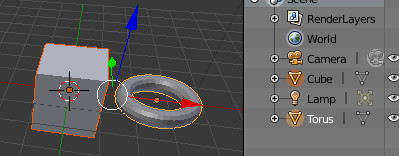
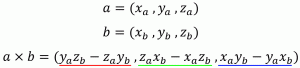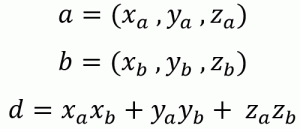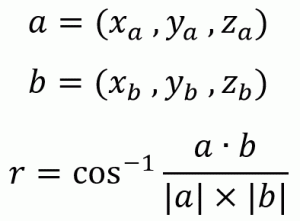vray for blender で Sun(Direct)
Direct Light Parameters (Google翻訳)
Direct - a simple directional light
直接 - 単純な指向性のある光
ということで、Directは太陽光というよりも指向性のライトという扱いです。
各パラメータの変更による結果の変化
①Intensity
とどのつまりはライトの強さです。
②Radius
ライトの径です
③Hotspot
Radius=10の時のhotspotの変化。
半径内の最も光の強い領域のサイズです
④Decay
別ページで掲載
WordPressのファイルの最大アップロードサイズを変更する
記事に画像などをアップロード出来ないことがあります。Wordpressの管理画面の「メディア」→「新規追加」の「最大アップロードサイズ」を上回るファイルはアップロード出来ません。
これが初期状態では2M等小さい値になっています。上限を上げる方法です。
php.iniか.htaccessを変更します。巷ではphp.iniのほうが多いですがそれでは効かない場合があります。やってみて動かなかったら.htaccessを編集しましょう。
ちなみに私はさくらレンタルサーバーを使っていますがphp.iniが効きませんでした。
次のいずれかを行います。
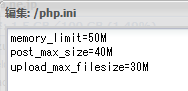
php.ini
追加内容：
post_max_size=40M
upload_max_filesize=30M
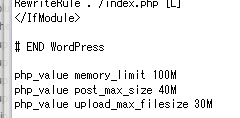
.htaccess
追加内容：
php_value post_max_size 40M
php_value upload_max_filesize 30M
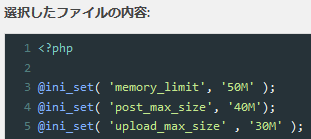
functions.php
追加内容：
@ini_set( 'post_max_size', '40M');
@ini_set( 'upload_max_size', '30M' );
functions.phpの場合、ini_set関数を使います。
ini_setはphp.iniの設定を変える関数です。
@はエラーを出力しないためにつけます。
http://php.net/manual/ja/function.ini-set.php
意味と注意
意味は、
- memory_limit ... スクリプトが確保できる最大メモリ
- post_max_size ... データに許可される最大サイズ
- upload_max_filesize ... アップロードできるファイルの最大サイズ
で、設定するサイズは以下の関係である必要があります。
C言語で、ある三次元ベクトルに垂直なベクトルを求める
C/C++で、ある三次元ベクトルに垂直なベクトルを求めます。
内積・外積を使うので、それらも定義する必要があります。
三次元ベクトルの外積
外積を求める式は、このようになります。
//! @brief 三次元ベクトルの外積を求める //! @param [out] dvec 求めたベクトル //! @param [in] svec1 一つ目の三次元ベクトル //! @param [in] svec2 二つ目の三次元ベクトル //! @return なし void outer(double * const dvec, double const * const svec1, double const * const svec2) { const double& xa = svec1[0]; const double& ya = svec1[1]; const double& za = svec1[2]; const double& xb = svec2[0]; const double& yb = svec2[1]; const double& zb = svec2[2]; dvec[0] = ya * zb - za * yb; dvec[1] = za * xb - xa * zb; dvec[2] = xa * yb - ya * xb; }
三次元ベクトルの内積
内積を求める式は、このようになります。
//! @brief ベクトルの内積を求める //! @param [in] vec1 一つ目の三次元ベクトル //! @param [in] vec2 二つ目の三次元ベクトル //! @return 内積 double inner(double const * const vec1, double const * const vec2) { const double& xa = vec1[0]; const double& ya = vec1[1]; const double& za = vec1[2]; const double& xb = vec2[0]; const double& yb = vec2[1]; const double& zb = vec2[2]; return (xa*xb + ya*yb + za*zb); }
三次元ベクトルの長さ
//! @brief ベクトルの長さを求める関数 //! @param [in] vec 三次元ベクトル //! @return 長さ double vlen(double const * const vec) { const double& x = vec[0]; const double& y = vec[1]; const double& z = vec[2]; return sqrt(x * x + y * y + z * z); }
二つの三次元ベクトルがなす角度（ラジアン）
//! @brief 二つのベクトルの角度をラジアンで求める関数 //! @param [in] vec1 一つ目の三次元ベクトル //! @param [in] vec2 二つ目の三次元ベクトル //! @return 二つのベクトルのなす角（ラジアン） double vangle(double const * const vec1, double const * const vec2) { return acos(inner(vec1, vec2) / (vlen(vec1) * vlen(vec2))); }
上記コードでは省いていますが、acosの引数の範囲は-1～1なので、この範囲を超えると定義域エラーとなります。実用する場合は何らかのエラー処理が必要になります。
ある三次元ベクトルに垂直なベクトルを求める
//! @brief ある三次元ベクトルに垂直な三次元ベクトルを求める //! @param [out] dst3 結果の格納先 //! @param [in] src3 三次元ベクトル void rightvec(double* dst3, double* src3) { double tmp[3] = { 1,0,0 }; //tmpとsrc3の角度０またはそれに近いなら、別なベクトルを用意 if (vangle(tmp, src3) < 0.00174533) { //0.00174533rad=1degree tmp[0] = 0; tmp[1] = 1; tmp[2] = 0; } //外積を求める outer(dst3, tmp, src3); }
ベクトルa,bの外積は、必ずa,b両方に対して垂直になります。
従って、あるベクトルuと、何でも良いからuとは違うベクトルvを用意し、その二つの外積wを求めると、必ずu⊥wとなります。計算が終わったらvは捨てて構いません。
ただし、u≠vでなければなりません。そこで上記プログラムでは、まずv(1,0,0)を用意します。もしuとvの角度が極めて０に近ければ、同じベクトルと考え、vを(0,1,0)に変更した後、外積を求めます
以下動作テスト
#include <Windows.h> #include <gl/GL.h> #include <gl/freeglut.h> #include <math.h> #pragma comment(lib,"opengl32.lib") #pragma comment(lib,"freeglut.lib")
void display(void) { glClear(GL_COLOR_BUFFER_BIT); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); glTranslated(0.0, 0.0, -5.0); glPushMatrix(); static double deg = 0; deg = deg + 1; glRotated(deg, 0, 1, 0); glColor3d(1, 0, 0); //一本目のベクトルを表示 double src3[3] = { 2,-3,4 }; glBegin(GL_LINES); glVertex3d(0, 0, 0); glVertex3dv(src3); glEnd(); glColor3d(0, 1, 0); double dst3[3]; rightvec(dst3, src3); //二本目のベクトルを表示 glBegin(GL_LINES); glVertex3d(0, 0, 0); glVertex3dv(dst3); glEnd(); glPopMatrix(); glFlush(); } void timer(int value) { glutPostRedisplay(); glutTimerFunc(50, timer, 0); } void init(void) { glClearColor(0.0, 0.0, 1.0, 1.0); } void resize(int w, int h) { glViewport(0, 0, w, h); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(30.0, (double)w / (double)h, 1.0, 100.0); } int main(int argc, char *argv[]) { glutInit(&argc, argv); glutInitDisplayMode(GLUT_RGBA); glutCreateWindow(argv[0]); glutDisplayFunc(display); glutReshapeFunc(resize); glutTimerFunc(100, timer, 0); init(); glutMainLoop(); return 0; }
C++のunordered_mapで自作クラスを使う (主にハッシュ値生成について)
概要
C++11以降、ハッシュマップ(hash map)の機能が追加されました。
しかしhash mapの名前の既存ライブラリがたくさんあったので、衝突しないようにunordered_mapという名前にしました。
で、このunorderd_mapは基本型ならそのまま使えるんですが、自作型の場合にはクラスのインスタンスからハッシュ値を作る機能も作ってやる必要があります。
サンプルコード
#include <string> #include <unordered_map> #include <iostream> //////////////////////////////////////////////////////////////// //ハッシュ値を統合する ( 汎用的に使用できる関数 ) // seed in:既存のハッシュ値 out:元のseedとvから作成したハッシュ値を統合した値 // v 新たにハッシュ値を作成する値 template<typename T> void hash_combine(size_t & seed, T const& v) { //基本型に関するハッシュ生成は標準ライブラリが提供している std::hash<T> primitive_type_hash; //生成したハッシュを合成する。このコードはboostものを使用する seed ^= primitive_type_hash(v) + 0x9e3779b9 + (seed << 6) + (seed >> 2); } //////////////////////////////////////////////////////////////// // 自作データ class MyData { public: std::string m_v_str; int m_v_int; double m_v_double; }; //////////////////////////////////////////////////////////////// // 自作データの比較演算子 bool operator==(const MyData& v1, const MyData& v2) { return v1.m_v_str == v2.m_v_str && v1.m_v_int == v2.m_v_int && v1.m_v_double == v2.m_v_double;//本当はdoubleを==比較してはいけません } //////////////////////////////////////////////////////////////// //自作データのハッシュを作成 namespace std { // 標準ライブラリは struct hash<>というデータをハッシュ化する関数オブジェクトのテンプレートを提供している // これは最初から基本型に対しては特殊化されているのでそのまま使える(上記hash_combine内で使用) // 自作クラスの場合は自分で特殊化し、operator()を定義してやる。 template<> struct hash<MyData> { public: size_t operator()(const MyData& data)const { //クラスのメンバの値それぞれについてハッシュ生成して、それらを結合して一つのハッシュ値にする std::size_t seed = 0; hash_combine(seed, data.m_v_str); hash_combine(seed, data.m_v_int); hash_combine(seed, data.m_v_double); return seed; } }; } //////////////////////////////////////////////////////////////// // エントリポイント int main() { std::unordered_map<MyData, int> map; map[ { "hello" , 111 , 6.0e3 } ] = 0; map[ { "goodbye" , 111 , 6.0e3 } ] = 0; map[ { "hello" , 222 , 6.0e3 } ] = 0; map[ { "goodbye" , 222 , 6.0e3 } ] = 0; map[ { "hello" , 222 , 2.0e4 } ] = 0; map[ { "goodbye" , 222 , 3.0e4 } ] = 0; for (int i = 0; i < 3; i++) { map[{"hello" , 111, 6.0e3 }]++; map[{"goodbye", 111, 6.0e3 }]++; } using namespace std; //結果出力 for (auto& data : map) { cout << "( " << data.first.m_v_str << " , " << data.first.m_v_int << " , " << data.first.m_v_double << " ) = " << data.second << std::endl; } int i; cin >> i; return 0; }
実行結果
( hello , 111 , 6000 ) = 3
( goodbye , 111 , 6000 ) = 3
( hello , 222 , 6000 ) = 0
( hello , 222 , 20000 ) = 0
( goodbye , 222 , 30000 ) = 0
要点
unorderd_mapのキーとなる値が
- 基本型やstd::string型の時 ... 何も考えずそのまま使える
- 基本型でないとき ... 基本型のハッシュ値をhash_combineで結合し一つのハッシュ値としてから使用する
std::hash
std::hashはハッシュを生成するクラス(コード上はstruct)のテンプレートです。
これはintやfloat等の基本型や、std::stringやstd::shared_ptr型等の(標準)ライブラリ型に対して特殊化がされており、それらの型のハッシュ値を作成できます。
hash_combine
boost Reference l- 1.55.0 Header <boost/functional/hash.hpp>
これはboostにあった関数です。この関数は、与えられたハッシュ値と、与えられたデータから作成した別のハッシュ値の二つを統合し、一つのハッシュ値を作成します。boostではハッシュ生成にboost::hash_valueという関数が使われています。自前実装するときはstd::hashで作成します。
Blender bpy でvertexとfaceとedgeを追加
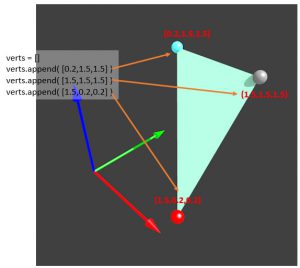
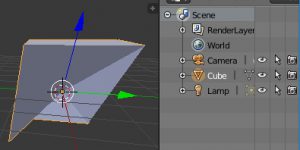
vertexを定義してfaceを追加
import bpy #頂点定義 verts = [] verts.append( [0.2,1.5,1.5] ) verts.append( [1.5,1.5,1.5] ) verts.append( [1.5,0.2,0.2] )
#面を、それを構成する頂点番号で定義 faces =[] faces.append( [0,1,2] )
#頂点と頂点番号からメッシュを作成 mymesh = bpy.data.meshes.new("mymesh") mymesh.from_pydata(verts,[],faces) #作成部分 mymesh.update()
#オブジェクトを作成し、メッシュを登録 obj = bpy.data.objects.new("My_Object", mymesh)
#オブジェクトのマテリアルを作成 mat = bpy.data.materials.new("Mat1") mat.diffuse_color = (0.3,0.7,0.5) obj.active_material = mat
#オブジェクトを登録 scene = bpy.context.scene scene.objects.link(obj)
#作成部分を以下のように変更すると、頂点の登録のみになります。
mymesh.from_pydata(verts,[],[])
エッジ用の頂点リストを作成したうえで、#作成部分を以下のように変更すると、エッジの登録のみになります。
edges = [] edges.append( [0,2] ) # エッジをなす二点の頂点番号 mymesh = bpy.data.meshes.new("mymesh") mymesh.from_pydata(verts,edges,[]) mymesh.update()
WordPressのカスタムフィールド追加（後編 データの保存）
６．コード
<?php /////////////////////////////////////////////////////////////// //カスタムフィールドの入力欄の中のデータをデータベースへ保存する function hook_func_for_save_customfield( $post_id ) { $areaname = "field_1"; $key = "_key_for_field_1"; ///// 正しい手段で送信されたデータであることを確認 //// //① nonceがセットされていなければ不正 if ( ! isset( $_POST[ 'nonce_for_field_1' ] ) ) return $post_id; //② nonceがセットされていても、自分で作成した値でないなら不正 if ( ! wp_verify_nonce( $_POST['nonce_for_field_1'] , 'send_field1' )) return $post_id; if ( ! current_user_can( 'edit_post', $post_id ) ) // ③ 書き込み権限がなければ不正 return $post_id; ///// カスタムフィールドの値を更新 /// $data = $_POST[$areaname]; if(get_post_meta($post_id, $key) == ""){ //新しいデータならデータを作成 add_post_meta($post_id, $key, $data, true); } elseif($data != get_post_meta($post_id, $key, true)){ //既存にあるデータで内容が異なるなら更新 update_post_meta($post_id, $key, $data); }elseif($data == ""){ //入力内容が空ならデータの削除 delete_post_meta($post_id, $key, get_post_meta($post_id, $key, true)); } return $post_id; } add_action( 'save_post', 'hook_func_for_save_customfield' ); ?>
７．動作
- save_postアクションフックにより、更新ボタンが押されたときにhook_func_for_save_customfield関数が実行されます。
- hook_func_for_save_customfield関数では、
①nonceがPOSTされ、
②かつその内容が発行した物と一致し、
③さらに書き込み権限があるときにのみ、次の処理を行います。 - 送信された値を元に、カスタムフィールドの値を、
・まだ値がなければ作成 ... add_post_meta関数で新規作成
・値はあるが内容が異なる ... update_post_metaで更新
・入力内容が空 ... delete_post_metaでデータから削除
を行います。
save_postアクションフック
save_post は投稿や固定ページが作成または更新されたとき実行されるアクションです。インポート、投稿や固定ページの編集画面、XMLRPC、メールによる投稿などがきっかけになります。投稿データは投稿の編集方法に応じて $_POST, $_GET またはグローバルの $post_data に保存されます。例えばクイック編集は $_POST を使います。
８．正しい点順で送信されたデータであることを確認
isset( $_POST[ 'nonce_for_field_1' ]
これはWordpressではなくPHPの世界の話です。
<input type="hidden" id="nonce_for_field_1" name="nonce_for_field_1" value="81b29b57b2" />
というフィールドをPOSTした場合、PHP側では
として受け取ります。issetは'nonce_for_field_1'という変数が送信されてきたかを確認します。nonceが正しいかを調べる前に、そもそも送られてきているかを調べるわけです。
変数がセットされており、それが
NULLでないことを調べます。
wp_verify_nonce関数
wp_nonce_fieldあるいはwp_create_nonceで生成したnonceと、送られてきたnonceが等しいかを検証する関数です。
nonce が正しいもので有効期限が切れていないことを、指定されたアクションとの関係も含めて確かめます。
$nonce, //送られてきたnonce
$action //生成時に指定したアクション
);
似た関数にcheck_admin_refereがありますが、現在は非推奨です。
バージョン 2.0.1 以降、リファラーがチェックされるのは $action 引数を省略（またはデフォルトの -1 をセット）したときだけですが、これは nonce を使わない後方互換性のためです。
つまりリファラーをチェックするときはnonceがチェックされず、nonceがチェックされるときはリファラーがチェックされない・・・ということでしょうか。
まとめると、wp_verify_noceとwp_nonce_fieldは、以下のように対応しています。
<?php //送信時 wp_nonce_field( 'send_field1' , 'nonce_for_field_1' ); ?>
<?php //受信時 wp_verify_nonce( $_POST['nonce_for_field_1'] , 'send_field1' ) ?>
current_user_can関数
ユーザーが権限を所有しているかどうかを調べます。
ページの編集の権利を持っているかどうかを調べるときは、'edit_pages'を指定します。
権限の一覧はこちらが詳しいです：
WordPress私的マニュアル current_user_can
９．カスタムフィールドの値を更新
get_post_meta関数で該当する価を取得します。get_post_meta関数の第三引数がfalseまたは省略した場合、カスタムフィールドの配列が返ります。trueを指定した場合は、配列の内容が全て一つの文字列となって返ります。
その結果に応じて、次の各関数を呼び出し追加・削除・更新を行います。
add_post_meta ($post_id, $key, $data, true);
add_post_meta() は、指定した投稿や固定ページへカスタムフィールド（「メタデータ」とも呼ばれます）を追加します。どんな投稿タイプの投稿でも構いません。ひとつのカスタムフィールドは、実際にはキーと値の組です。
update_post_meta($post_id, $key, $data);
update_post_meta() は、指定した投稿に存在するカスタムフィールドの値を更新します。add_post_meta() の代わりとしても使うことができます。この関数はまず、$post_id で ID を指定した投稿に $meta_key を持つカスタムフィールドが存在することを確認します。もし存在しなければ代わりに
add_post_meta( $post_id, $meta_key, $meta_value )を実行し、その結果を返します。
delete_post_meta($post_id, $key, get_post_meta($post_id, $key, true));
この関数は、投稿から指定したキー（もしくはキーと値）を持つカスタムフィールドをすべて削除します。update_post_meta()、get_post_meta()、add_post_meta() も見てください。
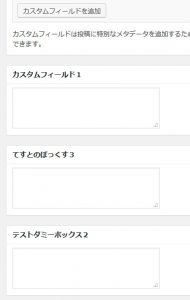
WordPressのカスタムフィールド追加（前編 メタボックス表示）
１．全貌
自分でカスタムフィールドを作成する場合、大きく分けて
- メタボックスを表示するコードの記述
- 値の読み込み/書き込みするコードの記述
の二つが必要になります。
まず、メタボックスを表示します。functions.phpに以下を記述します。
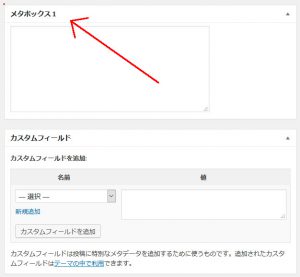
<?php //////////////////////////////////////////////////////////////////// //カスタムフィールドの見た目（入力欄等）を追加する function hook_func_for_metabox(){ // ① メタボックスの特性を定義する add_meta_box( 'metabox_div_id',//メタボックスのdivに指定されるID 'メタボックス１', //タイトル 'html_for_metabox_1_func', //表示用のHTMLを出力するphp関数（下で定義） 'post', //どのタイプの記事入力画面で表示するか 'normal', 'high' ); } // ② メタボックスの中身を実装する function html_for_metabox_1_func($post){ $areaname = "field_1"; $key = "_key_for_field_1"; echo '<textarea name="' . $areaname . '" rows="8" cols="60">' . get_post_meta($post->ID,$key,true) . '</textarea>'; // ③ nonceを作成し、hiddenフィールドとして書き込む wp_nonce_field( 'send_field1' , 'nonce_for_field_1' ); } // ④ カスタムフィールド用のメタボックスを追加する add_action('admin_menu', 'hook_func_for_metabox'); ?>
動作としては、
１．admin_menuアクションフックにより、管理画面が表示されたときにhook_func_for_metaboxが実行されます。
２．hook_func_for_metaboxの中で、メタボックスを追加するadd_meta_box関数が呼び出されます。そしてこの関数から、メタボックスの中身を描画するhtml_for_metabox_1_func関数が呼び出されます。
３．html_for_metabox_1_func関数内で、<textarea></textare>タグをechoし、入力欄を表示します。
これにより、投稿画面に「メタボックス１」というタイトルの、テキスト入力フィールドを一つ持つ領域（通称メタボックス）が作成されます。
２．admin_menuアクションフック
admin_menuアクションフックは、
管理画面メニューの基本構造が配置された後に実行する。
とのことです。
ちなみに、
この一行により、管理画面メニューが配置された後に、hook_func_for_metaboxが実行されるようになります。
ちなみに、add_meta_boxesアクションフックというのもあり、
こちらでもメタボックスを追加出来ます。この場合、下記add_meta_boxの$screenが'dashboard'など、引数によってはメタボックスが追加出来なくなります。
３．add_meta_boxによるメタボックスの定義
add_meta_boxはメタボックスを追加する関数です。
| 引数名 | 今回の例 | 意味 |
| $id | metabox_div_id |
例えばこのように出力されます： <div id="metabox_div_id"> ... </div> |
| $title | メタボックス１ |
タイトルです
|
| $callback | html_for_metabox_1_func | このメタボックスの中身を表示するための関数を指定します（後述） |
| $screen | post |
|
| $context | normal |
メタボックスの表示位置を指定します。
|
| $priority | high | (※) |
| $callback_args |
(※) 表示順と思われます。
<?php function hook_func_for_metabox(){ //メタボックスの特性を定義する add_meta_box( 'metabox_div_id', 'カスタムフィールド１', 'html_for_field1_func', 'post', 'advanced', 'low' ); add_meta_box( 'metabox_div_id_dummy', 'テストダミーボックス２', 'html_for_field1_func', 'post', 'advanced', 'high' ); add_meta_box( 'metabox_div_id_dummy2', 'てすとのぼっくす３', 'html_for_field1_func', 'post', 'advanced', 'high' ); } ?> |
 |
<?php function hook_func_for_metabox(){ //メタボックスの特性を定義する add_meta_box( 'metabox_div_id', 'カスタムフィールド１', 'html_for_field1_func', 'post', 'advanced', 'high' ); add_meta_box( 'metabox_div_id_dummy', 'テストダミーボックス２', 'html_for_field1_func', 'post', 'advanced', 'low' ); add_meta_box( 'metabox_div_id_dummy2', 'てすとのぼっくす３', 'html_for_field1_func', 'post', 'advanced', 'high' ); } ?> |
 |
４．メタボックスの中身の描画
html_for_metabox_1_funcの中ではHTMLをechoしているだけですが、重要な点がいくつかあります。
<?php //メタボックスの中身を実装する function html_for_field1_func($post){ $areaname = "field_1"; $key = "_key_for_field_1"; echo '<textarea name="' . $areaname . '" rows="3" cols="40">' . get_post_meta($post->ID,$key,true) . '</textarea>'; //nonceを作成し、hiddenフィールドとして書き込む wp_nonce_field( 'send_field1' , 'nonce_for_field_1' ); } ?>
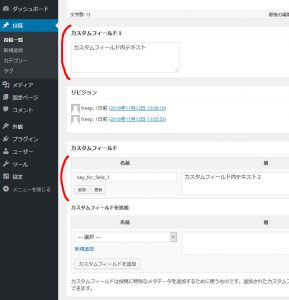
最も重要なのは_key_for_field_1という値で、これがいわゆる、カスタムフィールドの値が保存されている変数名です。
html_for_field1_funcでは<textarea>...</textarea>を表示しますが、その際に既に値が設定されていた場合はその値を表示したいので、get_post_meta関数で、現在のpostの_key_for_field_1の項目を取得して表示しています。
生成されるＨＴＭＬの例：
<textarea name="field_1" rows="3" cols="40"> この記事のカスタムフィールドの内容 </textarea>
注意として、_key_for_field_1のように、キー名は_ (アンダースコア)から始めた方が格好良いです。必須ではないですが、_から始まるキー名でないと、自分で追加したメタボックスの中だけでなく、投稿編集ページに最初からある「カスタムフィールド」の領域にもこのキーのカスタムフィールドの編集欄が出来てしまいます。害はないですが同じ物が二つあるのは気持ちが悪いので避けた方が良いでしょう。
参考 Codex 関数リファレンス/add post meta 見えない カスタムフィールドを作る
最後にwp_noce_fieldとwp_create_nonceですが、これらはセキュリティ的に必要なのでカスタムフィールドの書き込みと読み出しには直接関係はありません。従って省略可能ですが、普通セキュリティ対策は必須なので書きます。
５．wp_nonce_field
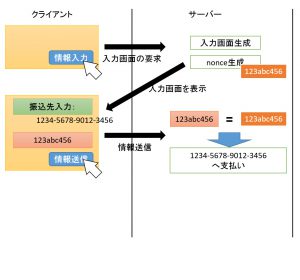
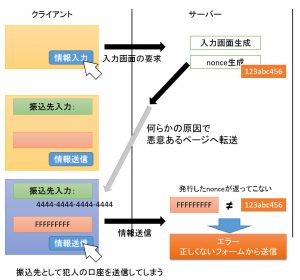
nonce（ノンス）は、ある種の誤使用や悪意のある操作から URL やフォームを守るための「一度だけ使われる数値」です。
私はセキュリティの専門家ではないのですが、もの凄くざっくりとした説明をすると以下のようになります。
|
成功した場合。 WordPress自分が発行したnonceと、「送信」ボタンが押されたときのnonceを比較し、その二つが等しければ 「この通信は、確かに自分が作成した送信フォームから送られた」 と結論します。 |
 |
|
失敗する場合。 何らかの理由により偽フォームに飛んでしまったような場合、そのフォームは自分のWordpressが作成したページではないので、発行したnonceも記載されていません。このフォームから送信した場合、送信されてくるnonce(あれば)と先ほど自分が発行したnonceが異なるので、 「この通信は、偽フォームから送られた」 と考えます。 |
 |
wp_nonce_fieldは、内部で wp_create_nonce 関数を呼び出しています。
wp_create_nonce
nonce を生成して返します。nonce は現在の時刻、$action 引数、現在のユーザー ID に基づいて生成されます。
つまり時間やユーザーや引数を元に、81b29b57b2のような文字列を作成します。そしてHTMLのhiddenフィールドとして出力します。
表記
出力
<input type="hidden" id="nonce_for_field_1" name="nonce_for_field_1" value="81b29b57b2" />
ここで、HTMLのformからPOSTでSubmitした場合、PHP側では
<?php if(isset($_POST[‘nonce_for_field_1’])){ $nonce = $_POST[‘nonce_for_field_1’]; echo $comment; //この結果は81b29b57b2 } ?>
と、$_POSTを使って受け取ることができます。
これで表示が終わったので、次回にはこのカスタムフィールドの値が「投稿」ボタンや「下書き」ボタンが押されたときにデータベースに保存するコードを記述します。
三次元オブジェクトをマウス回転(glut使用)
入門者がOpenGLを使う時、コードと出力結果だけでは何がどうなったのかわかりにくい事があります。
せめて回転ぐらいはしたいので、マウスの左ドラッグで描画対象を回転できるシンプルなコードを作成しました。
（例のごとく同種のものはいくらでもあると思います）
使い方：
マウス押下時に、dragstartを呼び出して回転開始を宣言します。
その後、マウスが動くたびにdragtoを呼び出して、回転状態を更新します。
最後、マウスボタンが離された時にdragendを呼び出して、回転の終了を宣言します。
球と直線の交差に関する式は
The Textbook of RayTracing @TDU
を参考にしました。
#pragma once #include <windows.h> #include <GL/gl.h> #include <GL/freeglut.h> #include "nurotate.h" #include "cube.h" int width, height; //回転オブジェクト定義 nu::mrotate camr; void disp(void) { glClear(GL_COLOR_BUFFER_BIT); glViewport(0, 0, width, height); glPushMatrix(); //原点を視線方向に0.5ずらす glTranslated(0, 0, -0.5); //回転行列を適用 double mat[16]; glMultMatrixd(camr.getmatrix(mat)); //一辺0.7のキューブを描画 cube(0.7); glPopMatrix(); glFlush(); } void reshape(int w, int h) { width = w; height = h; //クライアント領域のサイズを指定 //Win32APIの場合はGetClientRectで求めたrightとbottomだがglutではwとh camr.setWindowSize(width, height); //クライアント領域のどこの範囲に描画しているかを指定。 //glViewportで一画面丸々描画しているので、クライアント領域の(0,0)-(width,height)に書いていることになる camr.setRenderRect(0, 0, width, height); disp(); } //マウスクリック時のイベント void mouse(int button, int state, int x, int y) { if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) { camr.dragstart(x, y);//最初の回転軸を決定 } else if (state == GLUT_UP) { camr.dragend();//ドラッグ終了 } glutPostRedisplay(); } //ドラッグ時のイベント void motion(int x, int y) { camr.dragto(x, y);//移動中の回転軸を更新 disp(); } //エントリポイント int main(int argc, char ** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(400, 300); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("MouseRotateSample"); glutDisplayFunc(disp); glutReshapeFunc(reshape); glutMouseFunc(mouse); glutMotionFunc(motion); glutMainLoop(); return 0; }
呼出元のコードは見ての通りglutを使用していますが、freeglutを使っています。
また回転行列はglMultMatrixdで掛け合わせていますのでglRotate*等は使っていません。
#pragma once #include <cmath> namespace nu { //////////////////////////////////// //! @brief マウス回転用クラス class mrotate { double m_cam_matrix[16]; //!< @brief 現在の行列 double m_tmp_matrix[16]; //!< @brief マウス回転中に使用する一時的な行列 double m_vstart[3]; //!< @brief 回転スタート時の、「球の中心→"クリック位置のレイと球の交点"」 のベクトル double m_vend[3]; //!< @brief マウスが移動中の、〃 double m_raxis[3]; //vstartとvendの外積から算出した、回転中の回転軸(ベクトル) //viewportで指定した表示範囲をウィンドウ座標系で指定 int m_rectLTx, m_rectLTy; int m_rectRBx, m_rectRBy; //ウィンドウのサイズ int windowSizeX, windowSizeY; //マウスボタンが押されている間はtrueになり、trueの間は回転処理を行う bool m_fmousepush; public: mrotate(); ~mrotate(); //! @brief クライアント領域のサイズを指定する //! @param [in] width ウィンドウのクライアント領域の幅(ピクセル) //! @param [in] height ウィンドウのクライアント領域の高さ(ピクセル) void setWindowSize(const int width, const int height) { windowSizeX = width; windowSizeY = height; } //! @brief クライアント領域内にOpenGLで描画する範囲を矩形で指定。glviewportと同じだがこちらはクライアント座標系で矩形の四隅の座標を指定する void setRenderRect(int LeftTopX, int LeftTopY, int RightBottomX, int RightBottomY) { m_rectLTx = LeftTopX; m_rectLTy = LeftTopY; m_rectRBx = RightBottomX; m_rectRBy = RightBottomY; } //! @brief ドラッグ開始時に呼び出す //! @param [in] x クライアント座標系のマウスのx座標 //! @param [in] y クライアント座標系のマウスのy座標 //! @return なし void dragstart(int curx, int cury); //! @brief ドラッグ中に呼び出す //! @param [in] curx クライアント座標系のマウスのx座標 //! @param [in] cury クライアント座標系のマウスのy座標 //! @return なし void dragto(int curx, int cury); //! @brief ドラッグ終了時に呼び出す //! @return なし void dragend(); //! @brief 現在の回転行列を取得する const double* getmatrix(double* const dst)const; }; //////////////////////////////////// ///////////////////////////////////////////// //以下ベクトルと行列演算用の汎用的な関数//////// //三次元ベクトルの長さを求める inline double length3(const double* const vec3) { return std::sqrt(vec3[0] * vec3[0] + vec3[1] * vec3[1] + vec3[2] * vec3[2]); } //三次元ベクトルの外積を求める inline double inner3(const double * const vec1, const double * const vec2) { return ((vec1[0])*(vec2[0]) + (vec1[1])*(vec2[1]) + (vec1[2])*(vec2[2])); } inline void outer3(double * const dvec, double const * const svec1, double const * const svec2) { const double& x1 = svec1[0]; const double& y1 = svec1[1]; const double& z1 = svec1[2]; const double& x2 = svec2[0]; const double& y2 = svec2[1]; const double& z2 = svec2[2]; dvec[0] = static_cast<double>(y1 * z2 - z1 * y2); dvec[1] = static_cast<double>(z1 * x2 - x1 * z2); dvec[2] = static_cast<double>(x1 * y2 - y1 * x2); } inline double vangle3(double const * const vec1, double const * const vec2) { return acos(inner3(vec1, vec2) / (length3(vec1) * length3(vec2))); } inline void GetRotateMatrix(double* const m, const double radian, const double * const axis) { double s = sin(radian); double c = cos(radian); double len = length3(axis); double x = axis[0] / len; double y = axis[1] / len; double z = axis[2] / len; m[0] = x * x*(1 - c) + c; m[4] = x * y*(1 - c) - z * s; m[8] = x * z*(1 - c) + y * s; m[12] = 0; m[1] = x * y*(1 - c) + z * s; m[5] = y * y*(1 - c) + c; m[9] = y * z*(1 - c) - x * s; m[13] = 0; m[2] = x * z*(1 - c) - y * s; m[6] = y * z*(1 - c) + x * s; m[10] = z * z*(1 - c) + c; m[14] = 0; m[3] = 0; m[7] = 0; m[11] = 0; m[15] = 1; } inline bool normalize3(double * const pV) { double len; double& x = pV[0]; double& y = pV[1]; double& z = pV[2]; len = sqrt(x * x + y * y + z * z); if (len < 1e-6) return false; len = 1.0 / len; x *= len; y *= len; z *= len; return true; } inline double* CopyMat44(double* const dst16, const double* const src16) { for (int i = 0; i < 16; i++) { dst16[i] = src16[i]; } return dst16; } inline double* MultMatrix(double* const dst, const double* const m1, const double* const m2) { for (int i = 0; i < 16; i++) dst[i] = 0.0; double d1, d2; for (size_t j = 0; j < 4; j++) for (size_t k = 0; k < 4; k++) for (size_t c = 0; c < 4; c++) { d1 = m1[4 * j + c]; d2 = m2[4 * c + k]; dst[4 * j + k] += d1 * d2; } return dst; } inline double* MultMatrix(double* dst, const double* const src) { double m1[16]; for (int i = 0; i < 16; i++) { m1[i] = dst[i]; } MultMatrix(dst, m1, src); return dst; } inline void loadIdentity16(double * const mat) { for (int i = 0; i < 16; i++) { mat[i] = 0; } mat[0] = 1; mat[5] = 1; mat[10] = 1; mat[15] = 1; } }
前半はクラスの定義です。後半はベクトルや行列に関する演算用の汎用的な関数です。
#include "nurotate.h" #include <cstdio> namespace nu { mrotate::mrotate() { loadIdentity16(m_cam_matrix); loadIdentity16(m_tmp_matrix); m_fmousepush = false; } mrotate::~mrotate() { } const double* mrotate::getmatrix(double* const dst)const { CopyMat44(dst, m_cam_matrix); MultMatrix(dst, m_tmp_matrix); return dst; } void mrotate::dragstart(int curx, int cury) { //本来はマウスが押されている間に呼び出されることはない //もしそういうことが起こったら何もせずに抜ける if (m_fmousepush == true) return; //ドラッグ中であることを示す m_fmousepush = true; printf(" dragstart\n"); const long cx = (m_rectRBx - m_rectLTx) / 2;//開始点を左上と考えた時の、画面中央の座標 const long cy = (m_rectRBy - m_rectLTy) / 2;// const long x = curx - m_rectLTx - cx;//cx,cyを0と考えた時のマウスの座標(左下原点) const long y = (windowSizeY - cury) - m_rectLTy - cy; //球の半径 double r = std::fmin((m_rectRBx - m_rectLTx), (m_rectRBy - m_rectLTy)); //レイの方程式 p = s + td double s[3] = { (double)x,(double)y,-1000 }; double d[3] = { 0,0,1 }; double A = std::pow(length3(d), 2); double B = 2 * inner3(s, d); double C = std::pow(length3(s), 2) - r * r; double t1 = (-B + std::sqrt(B*B - 4 * A * C)) / (2 * A); double t2 = (-B - std::sqrt(B*B - 4 * A * C)) / (2 * A); //交点 double p[3] = { s[0] + t1 * d[0], s[1] + t1 * d[1], s[2] + t1 * d[2] }; normalize3(p); //中心→交点のベクトル m_vstart[0] = p[0]; m_vstart[1] = p[1]; m_vstart[2] = p[2]; } void mrotate::dragto(int curx, int cury) { //マウスドラッグ中でないなら何もしない if (m_fmousepush == false) return; printf(" dragend\n"); const long cx = (m_rectRBx - m_rectLTx) / 2;//開始点を左上と考えた時の、画面中央の座標 const long cy = (m_rectRBy - m_rectLTy) / 2;// const long x = curx - m_rectLTx - cx;//cx,cyを0と考えた時のマウスの座標(左下原点) const long y = (windowSizeY - cury) - m_rectLTy - cy; //球の半径 double r = std::fmin((m_rectRBx - m_rectLTx), (m_rectRBy - m_rectLTy)); //レイの方程式 p = s + td double s[3] = { (double)x,(double)y,-1000 }; double d[3] = { 0,0,1 }; double A = std::pow(length3(d), 2); double B = 2 * inner3(s, d); double C = std::pow(length3(s), 2) - r * r; double t1 = (-B + std::sqrt(B*B - 4 * A * C)) / (2 * A); double t2 = (-B - std::sqrt(B*B - 4 * A * C)) / (2 * A); //交点 double p[3] = { s[0] + t1 * d[0], s[1] + t1 * d[1], s[2] + t1 * d[2] }; normalize3(p); //中心→交点のベクトル m_vend[0] = p[0]; m_vend[1] = p[1]; m_vend[2] = p[2]; outer3(m_raxis, m_vstart, m_vend); normalize3(m_raxis); double angle = vangle3(m_vstart, m_vend) * 3; if (abs(angle) < 1e-6) return; GetRotateMatrix(m_tmp_matrix, angle, m_raxis); } void mrotate::dragend() { //マウスが押されている間しか処理しない if (m_fmousepush == false) return; //マウスドラッグが終わったことを示す m_fmousepush = false; MultMatrix(m_cam_matrix, m_tmp_matrix); loadIdentity16(m_tmp_matrix); } }
クラスの実装です。
Blender bpy で各データへアクセス
調査中のメモです。
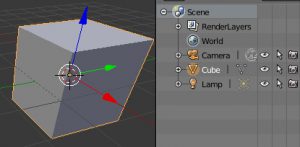
１．現在アクティブなオブジェクトへアクセス
import bpy; print ( bpy.context.active_object )
結果出力
結果出力
「アクティブなオブジェクト」というのはオレンジ色で強調されているもののことで、複数選択されているときも、アクティブなオブジェクトは一つだけです。
２．現在選択中のオブジェクトへアクセス
２．１ 選択中のオブジェクトを列挙
import bpy; print ( bpy.context.selected_objects )
結果出力
２．２ 選択中のオブジェクトの個数を取得
import bpy; print ( len(bpy.context.selected_objects) )
結果出力
３．オブジェクトの頂点へアクセス
３．１ オブジェクトの頂点の個数を取得
import bpy; print( len(bpy.context.active_object.data.vertices) )
結果出力
３．２ オブジェクトの頂点の座標を取得
import bpy; print( bpy.context.active_object.data.vertices[0].co )
結果出力
３．３ オブジェクトの頂点の座標を設定
import bpy bpy.context.active_object.data.vertices[ 0 ].co = [0.0,0.0,0.0]
実行結果
４．オブジェクトのエッジへアクセス
４．１ オブジェクトのエッジの個数を取得
import bpy; print( len(bpy.context.active_object.data.edges) )
結果出力
４．２ あるエッジを構成する頂点のインデクスを取得
import bpy; print( "vtx1 : " , bpy.context.active_object.data.edges[1].vertices[0] ) print( "vtx2 : " , bpy.context.active_object.data.edges[1].vertices[1] )
結果出力
vtx2 : 3
４．３ あるエッジを構成する頂点のインデクスから各座標を取得する
import bpy; print( "vtx1 : " , bpy.context.active_object.data.vertices[ bpy.context.active_object.data.edges[1].vertices[0] ].co ) print( "vtx2 : " , bpy.context.active_object.data.vertices[ bpy.context.active_object.data.edges[1].vertices[1] ].co )
結果出力
vtx2 : <Vector (-1.0000, 1.0000, -1.0000)>
glutのマウス操作
GLUTでのマウス操作一覧です。
#include <Windows.h> #include <gl/GL.h> #include <gl/freeglut.h> #pragma comment(lib,"opengl32.lib") #pragma comment(lib,"freeglut.lib") void disp(void) {} void mouse(int button, int state, int x, int y) { if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) { printf("left button down\n");//左ボタンダウン } if (button == GLUT_LEFT_BUTTON && state == GLUT_UP) { printf("left button up\n");//左ボタンアップ } if (button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN) { printf("right button down\n");//右ボタンダウン } if (button == GLUT_RIGHT_BUTTON && state == GLUT_UP) { printf("right button up\n");//右ボタンアップ } if (button == GLUT_MIDDLE_BUTTON && state == GLUT_DOWN) { printf("middle button down\n");//中ボタンダウン } if (button == GLUT_MIDDLE_BUTTON && state == GLUT_UP) { printf("middle button up\n");//中ボタンアップ } } //ドラッグ void motion(int x, int y) { printf("drag ... %d %d\n",x,y); } //ホイール void mouseWheel(int button, int dir, int x, int y) { if (dir > 0) { printf("wheel up\n"); } else { printf("wheel down\n"); } return; } int main(int argc,char** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(400, 300); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("mouse demo"); glutDisplayFunc(disp); glutMouseFunc(mouse); glutMotionFunc(motion); glutMouseWheelFunc(mouseWheel); glutMainLoop(); return 0; }