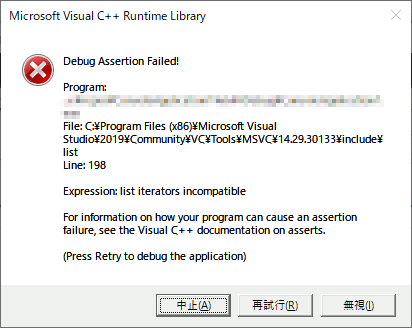
std::listを使っていてlist iterators incompatibleが出た。
以下のプログラムをデバッグモードで(←重要)走らせたところエラーが発生。
#include <iostream> #include <list> int main() { std::list<int> aa,bb; aa.push_back(0); bb.push_back(1); // 違うリストのイテレータを比較 if (aa.begin() == bb.begin()) std::cout << "same" << std::endl; }
原因と王道的な回避策
このエラーは、
・違うリストのイテレータ同士を比較し
かつ
・_ITERATOR_DEBUG_LEVEL==2の時
のとき起こる。だからデバッグーモードでは起こるがリリースモードでは起こらないということがありうる。
このエラーが出ている個所のコードを抜粋すると以下のようになっている。
_NODISCARD bool operator==(const _List_const_iterator& _Right) const noexcept { #if _ITERATOR_DEBUG_LEVEL == 2 _STL_VERIFY(this->_Getcont() == _Right._Getcont(), "list iterators incompatible"); #endif // _ITERATOR_DEBUG_LEVEL == 2 return this->_Ptr == _Right._Ptr; }
つまりイテレータのoperator==()の中でイテレータの正当性をチェックし、意味のない比較が行われたときは意図してエラーを出している。
従って、
などを指定してやれば回避できる。
ほかの解決方法を考える
この部分はイテレータの正当性をチェックし意図的に発生させているエラーなので、自前で書いてしまえばoperator==の前に検出できる。
#include <iostream> #include <list> int main() { std::list<int> aa,bb; aa.push_back(0); bb.push_back(1); std::list<int>::iterator i1 = aa.begin(); std::list<int>::iterator i2 = bb.begin(); #if _ITERATOR_DEBUG_LEVEL==2
// デバッグ時、異なるリスト同士の比較が生じる前にチェックする if (i1._Getcont() != i2._Getcont()) { std::cout << " i1 != i2 " << std::endl; } else
#endif
{ // デバッグ時、異なるリスト同士の比較が生じることはない if (i1 == i2) { std::cout << "i1 == i2" << std::endl; } else { std::cout << "i1 != i2" << std::endl; } }
}
ICUライブラリのicu::UnicodeStringを前方宣言したらC2757が発生
経緯
icuライブラリのラッパーを作成したくなり、hppにicu::UnicodeStringのポインタを持たせ、cpp内でnewする構造にした。この時、前方宣言したらエラーC2757が発生。原因はicuという名前空間が実は存在していないかららしい。
まず、エラーの出るコードは以下。
エラーの出るコード
icuwrap.hpp
#pragma once // クラスが名前空間に入っている時は前方宣言をこうする namespace icu{ // C2757 class UnicodeString; } // icu::UnicodeStringのラッパー struct MyICU { icu::UnicodeString* ustr; }; // ICUライブラリのUnicodeStringのラッパーを作成 MyICU make_my_icu(const char16_t* text);
icuwrap.cpp
#include <unicode/ucnv.h> #include <unicode/brkiter.h> #include"icuwrap.h" // 要リンク #pragma comment(lib, "icuuc.lib") #pragma comment(lib, "icudt.lib") MyICU make_my_icu(const char16_t* text) { MyICU tmp; tmp.ustr = new icu::UnicodeString(text); return tmp; }
main.cpp
#include "icuwrap.h" int main() { MyICU micu = make_my_icu(u"hello"); }
すると以下のコンパイルエラーが発生する
原因
構造
icuというリテラルは unicode/uversion.h の中で定義されているのだが、実はこれはU_ICU_NAMESPACEマクロで生成されたもののエイリアスで、さらにこれはU_ICU_ENTRY_POINT_RENAMEマクロで作成されている
unicode/uversion.h Line 105~
# define U_ICU_NAMESPACE U_ICU_ENTRY_POINT_RENAME(icu) namespace U_ICU_NAMESPACE { } namespace icu = U_ICU_NAMESPACE;
ではこの U_ICU_ENTRY_POINT_RENAME マクロの定義はというと、こちらは unicode/uvernum.h で定義されている。
unicode/uversion.h Line 128~
# define U_DEF_ICU_ENTRY_POINT_RENAME(x,y) x ## y # define U_DEF2_ICU_ENTRY_POINT_RENAME(x,y) U_DEF_ICU_ENTRY_POINT_RENAME(x,y) # define U_ICU_ENTRY_POINT_RENAME(x) U_DEF2_ICU_ENTRY_POINT_RENAME(x,U_ICU_VERSION_SUFFIX)
ここで ## はトークン結合演算子で、x は 「icu」、U_ICU_VERSION_SUFFIXは「_69」など、_ + ライブラリのバージョンが入っている
unicode/uversion.h Line 89
#define U_ICU_VERSION_SUFFIX _69
つまり「icu」は、「icu_69」のエイリアスである。
つまり
前方宣言で自分が定義した「namespace icu」というモノが既にあるのに、同じ「icu」をicu_69のエイリアスとして使おうとしたことになって、エラーが起こっている。
エラーの回避策
バージョンが固定でいいなら以下のように正規の名前空間で前方宣言すれば解決する
// クラスが名前空間に入っている時は前方宣言をこうする namespace icu_69{ class UnicodeString; } struct MyICU { icu_69::UnicodeString* ustr; }; // ICUライブラリのUnicodeStringのラッパーを作成 MyICU make_my_icu(const char16_t* text);
しかしどうせ隠すなら素直にpimplとして完全に隠す方がいい。
余談
U_DISABLE_RENAMINGマクロを使えば解決しそうに見えるが、マニュアルには「内部処理用だから使うな」と書いてあるのであきらめる。
OpenGL(GLSL)でfloat型のテクスチャを使う
rgbaがfloat[4]のテクスチャを使う。
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA32F, TEXWIDTH, TEXHEIGHT, 0,GL_RGBA, GL_FLOAT, texdata);
GL_RGBA32F,GL_RGBA,GL_FLOATを指定する。他はunsigned charの時と変わらない。
サンプル
#pragma comment(lib,"glew32s.lib") #define GLEW_STATIC #include <gl/glew.h> #include <GL/glut.h> GLuint ProgramID; GLuint FragmentShaderID; GLuint VertexShaderID; typedef GLfloat rgba_t[4]; //テクスチャ用 typedef GLfloat points_t[3]; //モデルの座標用 typedef GLfloat texcoord_t[2];//テクスチャ座標用 const int P_COUNT = 4; //頂点データ GLuint vertexbuffer; points_t position[P_COUNT]; //テクスチャ座標データ texcoord_t texcoord[P_COUNT]; GLuint texcoordbuffer; //テクスチャデータ rgba_t texdata[P_COUNT]; GLuint textureID; void prepare_buffers() { //テクスチャ(画像)作成 // 2*2の画像 texdata[0][0] = 1.0; texdata[0][1] = 0; texdata[0][2] = 0; texdata[0][2] = 0; texdata[1][0] = 0; texdata[1][1] = 1.0; texdata[1][2] = 0; texdata[0][2] = 0; texdata[0][2] = 0; texdata[2][0] = 0; texdata[2][1] = 0; texdata[2][2] = 1.0; texdata[0][2] = 0; texdata[3][0] = 1.0; texdata[3][1] = 1.0; texdata[3][2] = 1.0; texdata[0][2] = 0; ////////////////////////////////////////// ////////////////////////////////////////// //頂点座標の定義 (四角形) // いつもなら glVertex3fv等て指定するもの position[0][0] = -0.7; position[0][1] = 0.7; position[0][2] = 0; position[1][0] = -0.7; position[1][1] = -0.7; position[1][2] = 0; position[2][0] = 0.7; position[2][1] = -0.7; position[2][2] = 0; position[3][0] = +0.7; position[3][1] = +0.7; position[3][2] = 0; ////////////////////////////////////////// ////////////////////////////////////////// //テクスチャ座標の定義 //いつもならglTexCoord2f等で指定するもの texcoord[0][0] = 0; texcoord[0][1] = 1; texcoord[1][0] = 0; texcoord[1][1] = 0; texcoord[2][0] = 1; texcoord[2][1] = 0; texcoord[3][0] = 1; texcoord[3][1] = 1; ////////////////////////////////////////// ////////////////////////////////////////// //テクスチャの作成 // 普通のテクスチャ作成 glGenTextures(1, &textureID); glBindTexture(GL_TEXTURE_2D, textureID); int TEXWIDTH = 2; // 2*2の画素数 int TEXHEIGHT = 2; glPixelStorei(GL_UNPACK_ALIGNMENT, 1); // テクスチャの割り当て glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA32F, TEXWIDTH, TEXHEIGHT, 0,GL_RGBA, GL_FLOAT, texdata); // テクスチャを拡大・縮小する方法の指定 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST); ////////////////////////////////////////// ////////////////////////////////////////// //頂点バッファの作成 glGenBuffers(1, &vertexbuffer); glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer); glBufferData(GL_ARRAY_BUFFER, 3 * P_COUNT * sizeof(GLfloat), position, GL_STATIC_DRAW); //テクスチャ座標バッファの作成 glGenBuffers(1, &texcoordbuffer); glBindBuffer(GL_ARRAY_BUFFER, texcoordbuffer); glBufferData(GL_ARRAY_BUFFER, 2 * P_COUNT * sizeof(GLfloat), texcoord, GL_STATIC_DRAW); } void display(void) { glClearColor(0, 0, 0, 1); glClear(GL_COLOR_BUFFER_BIT); glDisable(GL_CULL_FACE);//カリングを無効にする /////////////////////////////////// // 行列の設定 glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(65, 1, 0.1, 10); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); glTranslated(0.0, 0.0, -3); /////////////////////////////////// // シェーダを使う glUseProgram(ProgramID); /////////////////////////////////// // 頂点バッファを有効化 glEnableVertexAttribArray(0); glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer); glVertexAttribPointer( 0, // 属性0 3, // 1要素の個数。GLfloatのx,y,zなので3 GL_FLOAT, // タイプ GL_FALSE, // 正規化しない(データが整数型の時) 0, // ストライド (void*)0 // 配列バッファオフセット ); /////////////////////////////////// //テクスチャ座標バッファの有効化 glEnableVertexAttribArray(1); glBindBuffer(GL_ARRAY_BUFFER, texcoordbuffer); glVertexAttribPointer( 1, // 属性1 2, // 1要素の個数。GLfloatのu,vなので2 GL_FLOAT, // タイプ GL_FALSE, // 正規化しない(データが整数型の時) 0, // ストライド (void*)0 // 配列バッファオフセット ); /////////////////////////////////// // 四角形の描画 glDrawArrays(GL_TRIANGLE_FAN, 0, P_COUNT); glDisableVertexAttribArray(0); glDisableVertexAttribArray(1); glFlush(); }
Assimpのテスト
非常に多くのモデルデータを読み込めるBSDライセンスのライブラリ。
ビルドはそんなに難しくないのでとりあえずサンプルコードを先に置いておく。
元のサンプルコード
http://assimp.sourceforge.net/lib_html/usage.html
Bunnyのデータ
https://commons.wikimedia.org/wiki/File:Stanford_Bunny.stl
なおstanford bunnyは(スケールが)大きいのでgluLookatで少し遠いところにカメラを設置している。
#include <iostream> #include <vector> #include <array> //////////////////////////// // 表示用のOpenGL // NOMINMAXをしておかないとmaterial.inlでstd::minでエラーが起こる #define NOMINMAX #include <Windows.h> #include <gl/GL.h> #include <gl/GLU.h> #include <gl/freeglut.h> //////////////////////////// // Assimp #include <assimp/Importer.hpp> // C++ importer interface #include <assimp/scene.h> // Output data structure #include <assimp/postprocess.h> // Post processing flags #pragma comment(lib,"assimp-vc142-mt.lib") //////////////////////////// //読み込んだポリゴンデータの格納先 std::vector<std::array<unsigned int, 3>> triangles; std::vector<std::array<float, 3>> points; ////////////////////////////
//! @brief メッシュファイルを読み込み //! @sa http://assimp.sourceforge.net/lib_html/usage.html bool MyDataImporter( std::vector<std::array<unsigned int, 3>>& faces, std::vector<std::array<float, 3>>& coords, const std::string& pFile) { // Create an instance of the Importer class Assimp::Importer importer; const aiScene* scene = importer.ReadFile(pFile, aiProcess_CalcTangentSpace | //接ベクトル空間を計算する aiProcess_Triangulate | //全ての面を三角形分割する aiProcess_JoinIdenticalVertices //重複頂点をマージする ); // If the import failed, report it if (!scene) { printf("失敗:%s\n", importer.GetErrorString()); return false; } if (scene->HasMeshes()) { //メッシュの配列 aiMesh** p = scene->mMeshes; //最初のメッシュへアクセス aiMesh* mesh0 = p[0];
//三角形一覧取得 int face_count = mesh0->mNumFaces; for (size_t findex = 0; findex < face_count; findex++) { aiFace& face = mesh0->mFaces[findex]; if (face.mNumIndices == 3) { faces.push_back( std::array<unsigned int, 3>{ face.mIndices[0], face.mIndices[1], face.mIndices[2] } ); } }
//頂点一覧取得 int vertex_count = mesh0->mNumVertices;
for (size_t vindex = 0; vindex < vertex_count; vindex++) {
aiVector3D& vtx = mesh0->mVertices[vindex]; coords.push_back( std::array<float, 3>{vtx.x, vtx.y, vtx.z} );
} } // 終了(解放不要) return true; }
//ウィンドウの幅と高さ int width, height; //描画関数 void disp(void) { glViewport(0, 0, width, height); glClearColor(0.2, 0.2, 0.2, 1); glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glMatrixMode(GL_PROJECTION); glLoadIdentity(); gluPerspective(45, 1, 0.1, 500); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); gluLookAt( 100, 200, 100, 0, 0, 50, 0, 0, 1); glEnable(GL_CULL_FACE); double v = 0.7; glColor3d(1, 0, 0); for (size_t f = 0; f < triangles.size(); f++) { int p0 = triangles[f][0]; int p1 = triangles[f][1]; int p2 = triangles[f][2]; glBegin(GL_LINE_LOOP); glVertex3fv(points[p0].data()); glVertex3fv(points[p1].data()); glVertex3fv(points[p2].data()); glEnd(); } glEnd(); glFlush(); } //ウィンドウサイズの変化時に呼び出される void reshape(int w, int h) { width = w; height = h; disp(); } //エントリポイント int main(int argc, char** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(500, 500); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("sample"); glutDisplayFunc(disp); glutReshapeFunc(reshape); std::string f = R"(D:\dev\Stanford_Bunny.stl)"; MyDataImporter(triangles, points, f); glutMainLoop(); return 0; }
実行結果
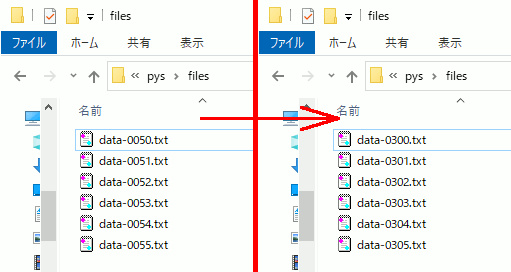
連番ファイル名の番号をシフトするpythonスクリプト
import os import random, string
# @brief ダミーファイル名を作成 # @details 処理時、一度この名前でファイルを書き換えてから目的の名前に変更する # @sa https://qiita.com/Scstechr/items/c3b2eb291f7c5b81902a def create_random_filename(): n = 10 dummy = '' while True: dummy = ''.join(random.choices(string.ascii_letters + string.digits, k=n)) # 生成した文字列をファイル名とするファイルが存在しなければ処理を終了 if os.path.exists(dummy) == False: break return dummy
# @brief ファイル名の変更規則一覧作成 # @param [in] _format_ ファイル名の書式 # @param [in] _range_ 元のファイルの番号の範囲 # @param [in] _new_offset_ 新しい番号の先頭番号 # @return [ 現在のファイル名 , ダミーファイル名 , 変更後のファイル名 ] のリスト def sequence_filename( _format_ , _range_, _new_offset_ ): Li=[] dir = os.path.dirname( _format_ ) + "/" for i in _range_: # 変更したい対象のファイル名を作成 fname = _format_ % i retfname = _format_ % (_new_offset_ + i - _range_[0])# 新たなファイル名を作成 # ランダムなファイル名作成 dummyname = dir + create_random_filename() Li.append([fname,dummyname,retfname]) return Li
def filename_shift( _format_ , _start_,_stop_, _new_offset_): Li = sequence_filename( _format_ , range(_start_,_stop_+1), _new_offset_ ) # 現在のファイル名 → ダミーファイル名 for j in Li: os.rename(j[0],j[1]) # ダミーファイル名 → 目的のファイル名 for j in Li: os.rename(j[1],j[2])
############################################ ############################################ ############################################ # 50番~のファイル名を300番~に変更 filename_shift( "files/data-%04d.txt" , 50,55,300 )
Windowsのゴミ箱にあまりにも大量のファイルを入れすぎて迂闊に表示もできなくなった場合の対応
状況
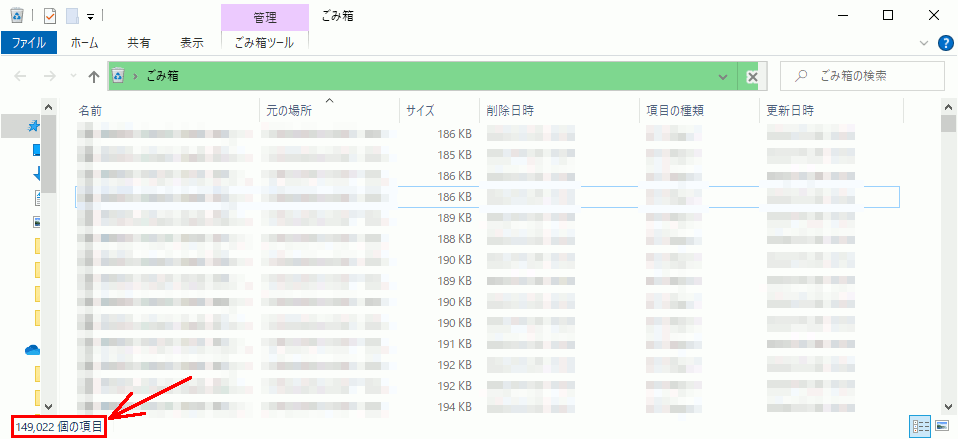
ファイルを捨てすぎて、ゴミ箱を開くのすら数分~数十分かかるような場合。
下手にゴミ箱から直接ファイルを削除しようものならOSごとフリーズする(復帰不可)。
しかもフリーズしたからと電源を落とすと「起動ドライブが見つかりません」のようなメッセージが出てドライブが認識できなくなる(電源落としてしばらく放置で解消を確認)
という事態に職場のPCで(←重要)陥り、とりあえず確実に安全と言えそうな手段を模索している。
なお上記図では149,022個の項目とあるが、これでもだいぶ減らした。
目的
1.ゴミ箱を再び使えるようにする。
2.ゴミ箱に圧迫されているドライブの領域を解放する
3.安全に対処する。上記1,2を満たす限り、安全でさえあれば他はどうでもいい。
手順
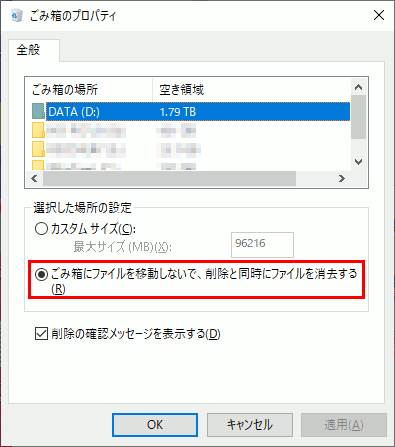
1.ファイルをゴミ箱に入れずに削除する設定にする
必須ではないが、Shiftを押しながら削除では押し忘れてゴミ箱に逆戻りしてしまう可能性があるので設定を変更しておいた方が無難。
2.別の空フォルダを用意
3.ゴミ箱を開き、ファイル一覧が表示された時点で読み込みを中断する
ゴミ箱の中身のファイル一覧は全て読み込まれなくてもある程度で一覧表示がされる。完全に終わらせようと待っているとそれだけでフリーズする。とりあえず一覧が出てファイルが多少なりとも見えた時点で読み込みを中止する。
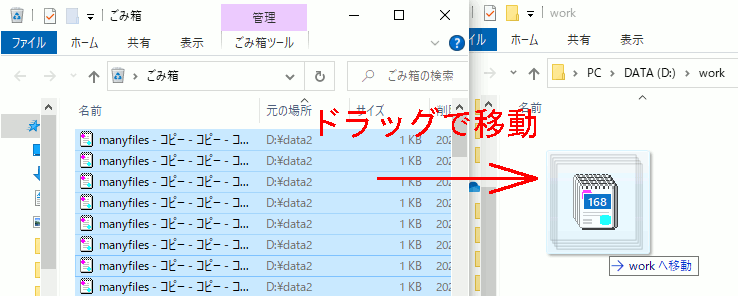
4.先に用意した空フォルダへゴミ箱のファイルを数千件だけ移動
私の環境を基準に言えば、一度に5000件以上はやらない方がいい。
5.フォルダごと削除
ゴミ箱に移動せずに削除する設定をしていない場合、Shiftキーを押しながら削除する。
6.2~4を繰り返す
感想
1.このトラブルは、「一つのフォルダの中に」ファイルが大量に入っていると処理が異常に重くなるらしいことが恐らくは重要である。
2.なお今回のゴミ箱はDドライブの物だったのだが、作業中どんどんCドライブの空き容量が減っていったので、恐らくはページファイルが作成されている。フリーズの原因か。
3.そういえばリストボックスは項目数が多くなると挙動が非常に重くなるので、扱う件数が非常に多いことが想定される場合はオーナードローリストボックスを使えとWindowsプログラミングでは言われている。
4.右クリックで「ごみ箱を空にする」ではどうなのか。怖くて試していない。
cudaMalloc/cudaFreeをcuda DLLの外側から呼び出す
mallocしたメモリはfreeするまで解放されない。それは知っている。
知っているが、CUDAプログラムをdll化した場合、まさかdll内関数から出た瞬間に自動解放されたりしないだろうな・・・?
という不安が頭をよぎったのでテスト。
以下、gpu_my_allocやdevice_to_hostなどは全てcuファイル内に書かれている。
C++側から別個に呼び出してもちゃんと動作するらしい。
C++側
#include <iostream> #pragma warning(disable:4996) #include "../CudaRuntime1/mytest.h" #pragma comment(lib,"CudaRuntime1.lib") void pnmP3_Write(const char* const fname, const int vmax, const int width, const int height, const unsigned char* const p); int main() { data_t dat; dat.width = 100; dat.height = 50; unsigned char *c = new unsigned char[dat.width * dat.height * 3]; for (size_t i = 0; i < dat.width * dat.height; i++) { c[i * 3 + 0] = 0; c[i * 3 + 1] = 0; c[i * 3 + 2] = 255; } dat.rgbdata = c; //GPU側メモリ確保 void* device = gpu_my_alloc(dat.width, dat.height); //GPU側へデータ転送 host_to_device(&dat, device); //処理実行 func_inverse(dat.width, dat.height, device); //CPU側へ結果を返却 device_to_host(device, &dat); //GPU側のメモリ解放 gpu_my_free(device); pnmP3_Write("test.ppm", 255, dat.width, dat.height, dat.rgbdata); } ///////////////////////////////////////////// //画像ファイル書き出し///////////////////////// //! @brief PPM(RGB各1byte,カラー,テキスト)を書き込む //! @param [in] fname ファイル名 //! @param [in] vmax 全てのRGBの中の最大値 //! @param [in] width 画像の幅 //! @param [in] height 画像の高さ //! @param [in] p 画像のメモリへのアドレス //! @details RGBRGBRGB....のメモリを渡すと、RGBテキストでファイル名fnameで書き込む void pnmP3_Write(const char* const fname, const int vmax, const int width, const int height, const unsigned char* const p) { // PPM ASCII FILE* fp = fopen(fname, "wb"); fprintf(fp, "P3\n%d %d\n%d\n", width, height, vmax); size_t k = 0; for (size_t i = 0; i < (size_t)height; i++) { for (size_t j = 0; j < (size_t)width; j++) { fprintf(fp, "%d %d %d ", p[k * 3 + 0], p[k * 3 + 1], p[k * 3 + 2]); k++; } fprintf(fp, "\n"); } fclose(fp); }
CUDA側
mytest.h
#ifdef __DLL_EXPORT_DO #define DLL_PORT extern "C" _declspec(dllexport) #else #define DLL_PORT extern "C" _declspec(dllimport) #endif struct data_t { int width; int height; unsigned char* rgbdata; }; //GPU側メモリ確保 DLL_PORT void* gpu_my_alloc(int width, int height); //処理実行 DLL_PORT void func_inverse(int width,int height, void* device); //GPU側へデータ転送 DLL_PORT void host_to_device(data_t* host, void* device); //CPU側へ結果を返却 DLL_PORT void device_to_host(void* device, data_t* host); //GPU側のメモリ解放 DLL_PORT void gpu_my_free(void* gpuptr);
mytest.cu
#include "cuda_runtime.h" #include "device_launch_parameters.h" #include <stdio.h> #include "mytest.h" struct gpudata { int width; int height; unsigned char* c; }; __device__ void color_inverse(unsigned char* c, int width, int height) { c[0] = 255 - c[0]; c[1] = 255 - c[1]; c[2] = 255 - c[2]; } __global__ void thread_inverse(gpudata data) { //このスレッドが担当する画素の位置を二次元座標で求める size_t xpos = blockIdx.x * blockDim.x + threadIdx.x; size_t ypos = blockIdx.y * blockDim.y + threadIdx.y; if (xpos < data.width && ypos < data.height) { size_t pos = (ypos * data.width + xpos) * 3; unsigned char* c = data.c + pos; // この関数はfunction.cuで定義されている color_inverse(c, xpos, ypos); } } void func_inverse(int width, int height, void* device){ // 16*16 == 256 < 512 int blockw = 16; int blockh = 16; dim3 block(blockw, blockh); int gridw = width / blockw + 1; int gridh = height / blockh + 1; dim3 grid(gridw,gridh); gpudata gpud; gpud.width = width; gpud.height = height; gpud.c = (unsigned char*)device; thread_inverse<<<grid,block>>> (gpud);//GPU側の関数を呼出 } void host_to_device(data_t* host, void* device) { cudaMemcpy( device, host->rgbdata, host->width * host->height * 3, cudaMemcpyHostToDevice);//GPU側へ処理したいデータを転送 } void device_to_host(void* device, data_t* host) { cudaMemcpy( host->rgbdata, device, host->width * host->height * 3, cudaMemcpyDeviceToHost);//GPU側から実行結果を取得 } void* gpu_my_alloc(int width, int height) { unsigned char* g_gpu; cudaMalloc( (void**)&g_gpu, width * height * 3);//GPU側メモリ確保 return g_gpu; } void gpu_my_free(void* gpuptr) { cudaFree(gpuptr);//GPU側のメモリを解放 }
GLFW3でタイマー(と同じ事)を使う
glfw3にはタイマー、つまり指定した時間が経ったら呼び出されるコールバック関数を指定するような機能が無い。従ってループ内でglfwGetTime()関数で現在時刻を秒単位で取得し、前回時刻取得時から目的の秒数だけ経ったら処理を実行することでタイマーと同じ効果を出す。
#include <cstdlib> #include <iostream> #include <Windows.h> #include <gl/GL.h> #include <GLFW/glfw3.h> #pragma comment(lib,"opengl32.lib") #pragma comment(lib,"glfw3.lib") int main() { //////////////////////////////////////////////////////////////////////////////// // GLFW の初期化 if (glfwInit() == GL_FALSE) { // 初期化に失敗したら終了 return 1; } //////////////////////////////////////////////////////////////////////////////// // ウィンドウを作成 GLFWwindow* window = glfwCreateWindow( 400, //width 400, //height "window title",//title NULL, //monitor NULL //share ); //////////////////////////////////////////////////////////////////////////////// // ウィンドウを作成できなければ終了 if (window == nullptr) { glfwTerminate(); return 1; } glfwMakeContextCurrent(window);
double prev = glfwGetTime(); const double TIME = 0.1;
int angle = 0; while (glfwWindowShouldClose(window) == GL_FALSE) { int width, height; glfwGetFramebufferSize(window, &width, &height); ///////////////////// // 描画 glViewport(0, 0, width, height); glOrtho(-1, 1, -1, 1, -1, 1); glClearColor(0, 0, 0, 1); glClear(GL_COLOR_BUFFER_BIT); glLoadIdentity(); glPushMatrix();
// glfwGetTime()で現在時刻を秒で取得 double now = glfwGetTime(); // 現在時刻 - 前回更新時刻 が TIME秒より開いていたら // 定期的に行いたい処理を実行する if (now - prev > TIME) { prev = now; // 前回更新時刻更新 // ここで関数呼び出しなど必要な処理を行う // 今回はangleを増加するのみ。 printf("angle %d\n",angle); angle += 15; }
glRotatef(angle, 1, 0, 0); glBegin(GL_QUADS); glColor3d(1, 0, 0); glVertex2d(-0.7, -0.7); glColor3d(0, 1, 0); glVertex2d(-0.7, 0.7); glColor3d(0, 0, 1); glVertex2d(0.7, 0.7); glColor3d(1, 1, 1); glVertex2d(0.7, -0.7); glEnd(); glPopMatrix(); glFlush(); glfwSwapBuffers(window); // イベント取得 //glfwWaitEvents(); glfwPollEvents(); } glfwTerminate(); }
Ubuntu 22.04でFirefoxが起動できなかったので設定変更
firefoxを起動しようとしたら謎の長いエラーが出た。
user:~$ firefox
Gtk-Message: 20:10:15.794: Failed to load module "canberra-gtk-module"
Gtk-Message: 20:10:15.795: Failed to load module "canberra-gtk-module"
ATTENTION: default value of option mesa_glthread overridden by environment.
ATTENTION: default value of option mesa_glthread overridden by environment.
ATTENTION: default value of option mesa_glthread overridden by environment.
(firefox:14675): Gdk-WARNING **: 20:10:17.713: The program 'firefox' received an X Window System error.
This probably reflects a bug in the program.
The error was 'BadAlloc'.
(Details: serial 527 error_code 11 request_code 146 (unknown) minor_code 7)
(Note to programmers: normally, X errors are reported asynchronously;
that is, you will receive the error a while after causing it.
To debug your program, run it with the GDK_SYNCHRONIZE environment
variable to change this behavior. You can then get a meaningful
backtrace from your debugger if you break on the gdk_x_error() function.)
Exiting due to channel error.
対応
セーフモードで起動
ハードウェアアクセラレーションの無効化
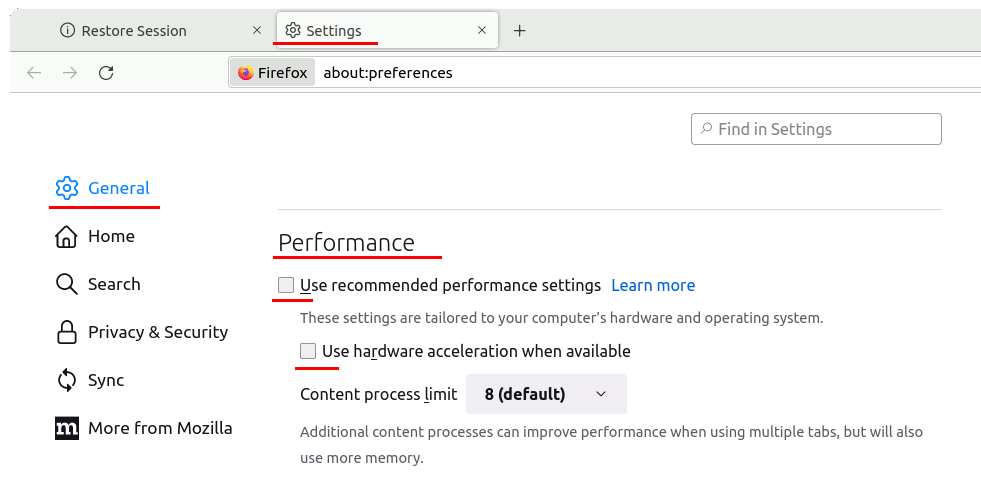
Performance → Use recommended performance setting → Use hardware acceleration when available
のチェックを外す。
CUDAのベクトル型を加減乗除する演算子
CUDAにはfloat3型などのベクトル型はあるが、ベクトル同士を計算する+,-などの演算子は定義されていない。
ではどうするかというと、CUDAのサンプルの中にhelper_math.hがあるので、これをダウンロードしてプロジェクトに追加する。
ダウンロード
https://github.com/NVIDIA/cuda-samples
導入
cuda-samples-master/Common/helper_math.h
使用例
#include "helper_math.h" // helper_math.h でincludeされているので不要 // #include "cuda_runtime.h" #include "device_launch_parameters.h" float3 my_calc(float3 a, float3 b) { return a + b; }