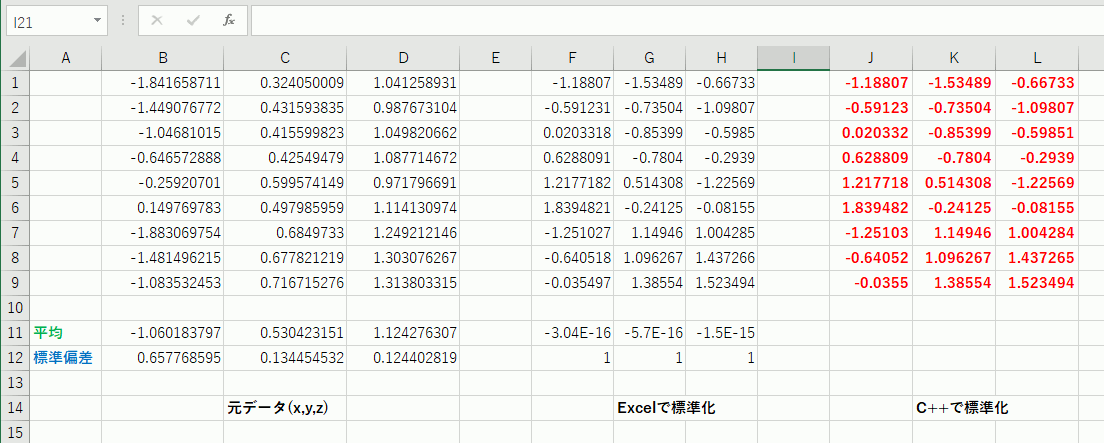
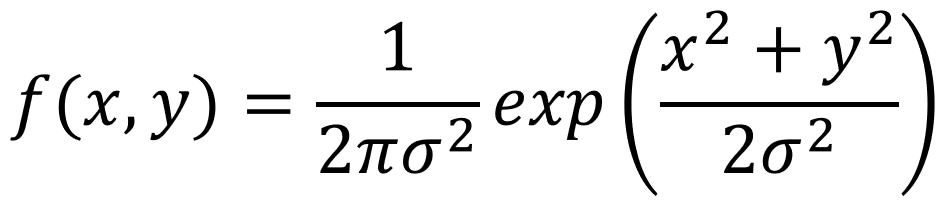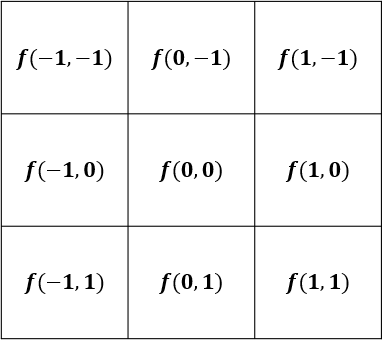Blenderのテクスチャを渦巻にする理屈
前に試したBlenderのボリュームで銀河を作るやつで、テクスチャを渦巻状にしていた。
Create a Galaxy in Blender – Iridesiumを試す(1)
改めて説明しろと言われるとやりにくいのでまとめておく。
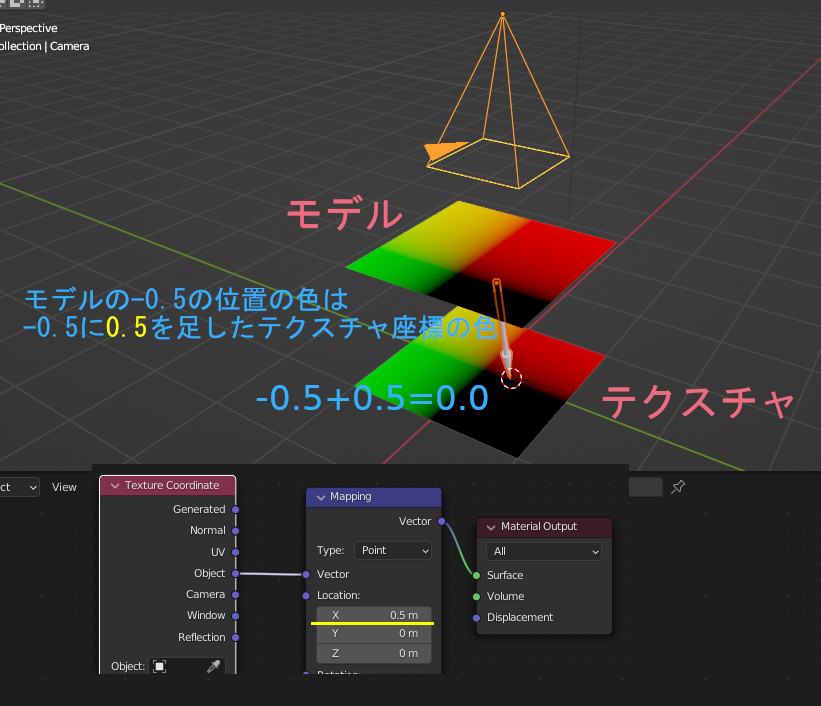
モデルにテクスチャが張り付いているとき、モデル上のある点の色は、テクスチャ上のどこかからとってきている。従って、テクスチャ座標を変換することでずらしたりできる。
テクスチャ座標をただ回転させただけでは、テクスチャが回るだけで渦巻にはならない。
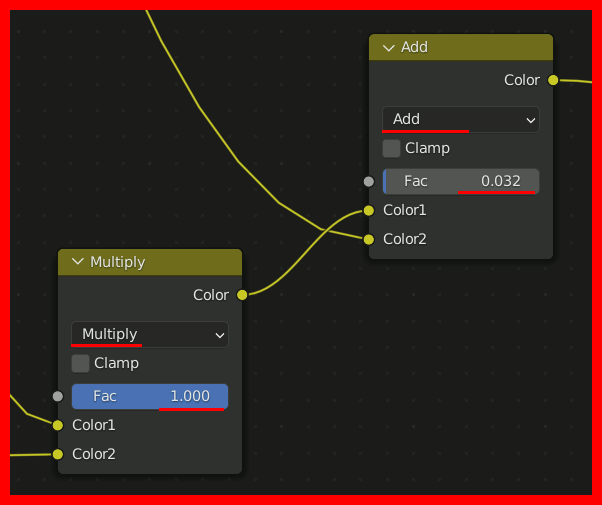
テクスチャが回転するだけなのは、モデル上の全ての位置で、同じ回転量だけ変化させてテクスチャの色をとってくるからで、つまり、モデル上の場所によって回転量を変化させれば、歪んだ座標系の色が取得できる。
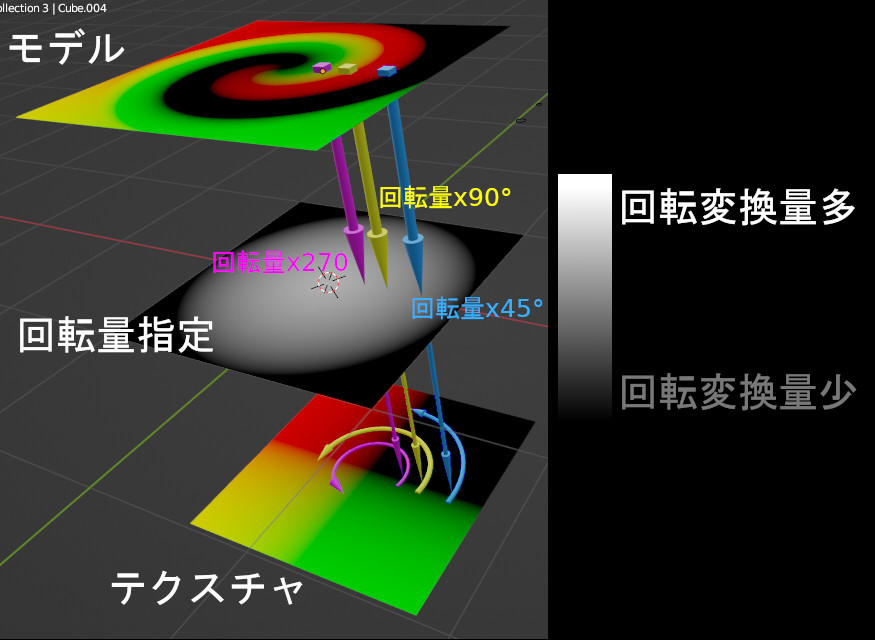
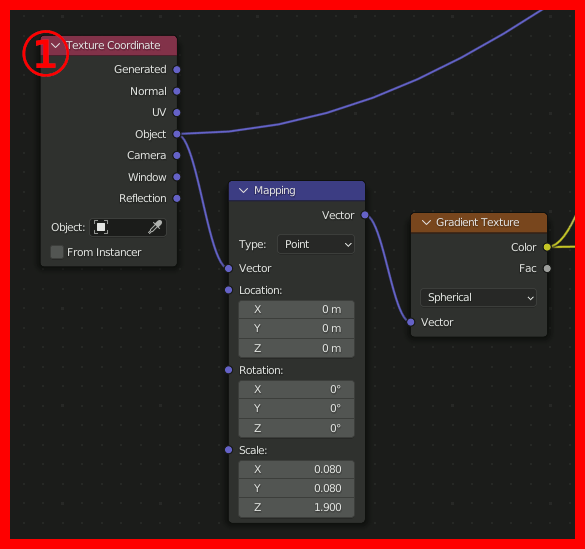
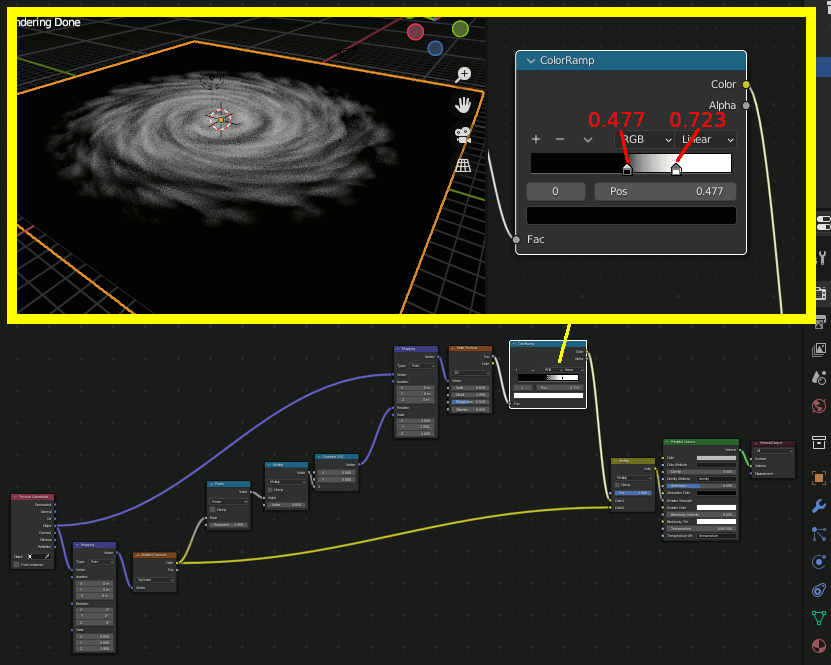
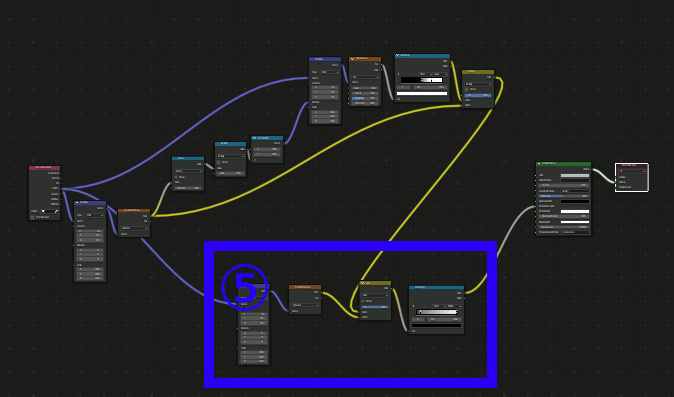
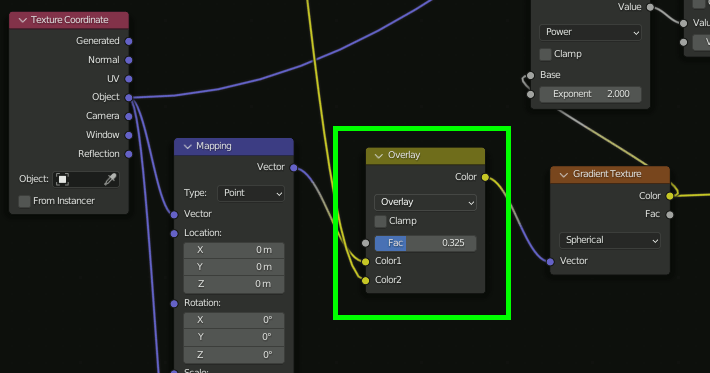
モデル上のある点の色を決めるとき、「テクスチャのどの位置から色をとってくるか」を求める際に、その座標をアフィン変換してやるのがmappingで、そこで回転を指定し、回転量としてGradientTextureを与えることで、場所によって回転量を変化させることができる。
Win32api でクリップボードにデータがコピーされたら動くプログラム
クリップボードを監視する方法を調べてみたら、AddClipboardFormatListenerにウィンドウハンドルを渡しておけば、クリップボードにコピーが発生するたびにWM_CLIPBOARDUPDATEメッセージが入ってくることが分かったのでこれを使うとクリップボードを管理するようなプログラムを書ける。
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam) { switch (message) { case WM_CREATE: // クリップボード監視開始 AddClipboardFormatListener(hWnd); return 0; case WM_CLIPBOARDUPDATE: // クリップボードが使用されるとこのメッセージが入る if (OpenClipboard(hWnd)) { // クリップボードの内容がテキストの時だけ処理 if ((IsClipboardFormatAvailable(CF_TEXT) == TRUE)) { HGLOBAL hg = GetClipboardData(CF_TEXT); size_t size = GlobalSize(hg); LPVOID strClip = GlobalLock(hg); char* strText = new char[size]; strcpy(strText, (char*)strClip); //クリップボード後始末 GlobalUnlock(hg); CloseClipboard(); // 表示 HDC hdc = GetDC(hWnd); RECT rect{ 0,0,100,100 }; DrawTextA(hdc, (char*)strText, -1, &rect, DT_LEFT); ReleaseDC(hWnd, hdc); } } return 0; case WM_LBUTTONDOWN: return 0; case WM_DESTROY: // クリップボード監視終了 RemoveClipboardFormatListener(hWnd); PostQuitMessage(0); break; case WM_PAINT: { PAINTSTRUCT ps; HDC hdc = BeginPaint(hWnd, &ps); EndPaint(hWnd, &ps); } break; default: return DefWindowProc(hWnd, message, wParam, lParam); } return 0; }
このコードは、クリップボードに文字列がコピーされると画面にその内容を表示する。
Create a Galaxy in Blender – Iridesiumを試す(2)
前回
Create a Galaxy in Blender – Iridesiumを試す(1)
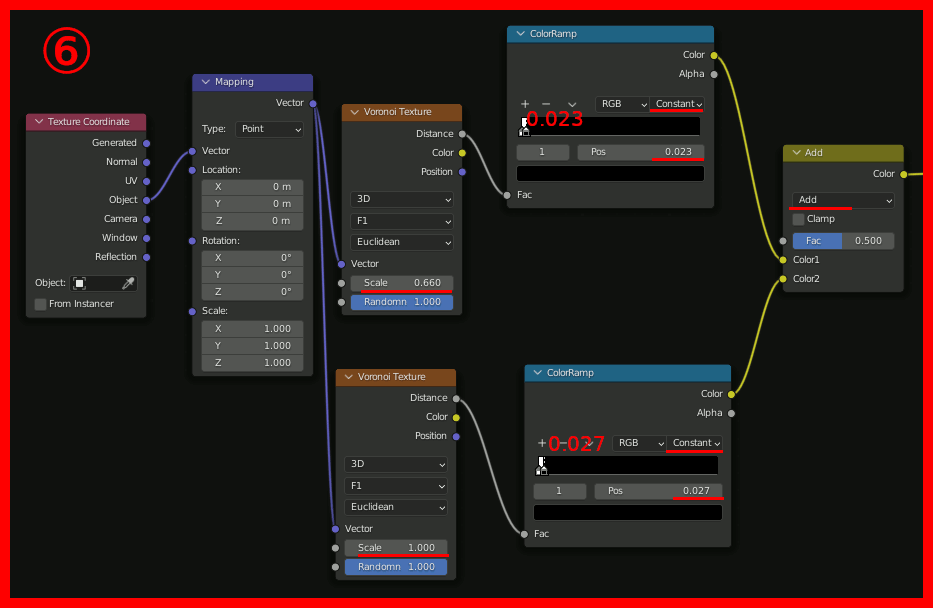
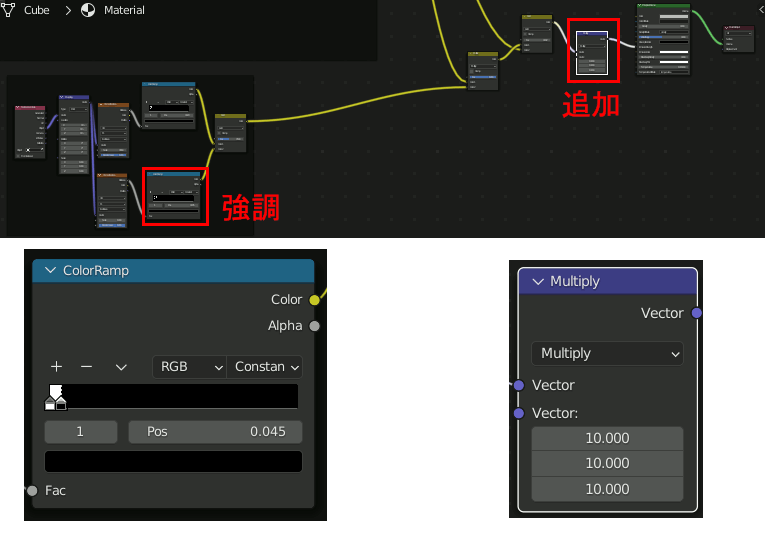
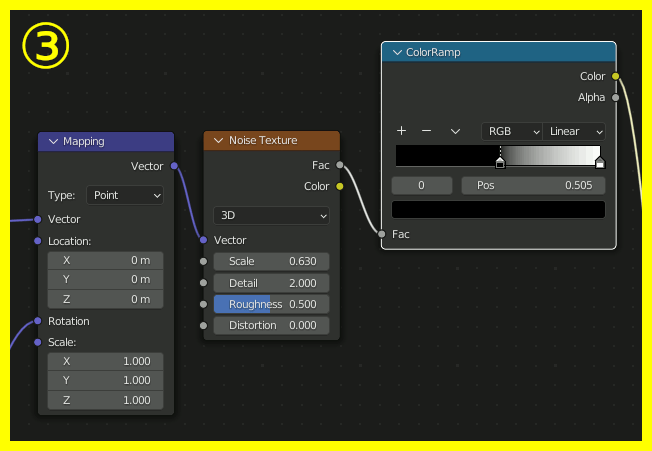
小さな星をちりばめるテクスチャを作成。
注意:あまりに見えづらい場合は強調させて作業を進める。(動画には入っていない)
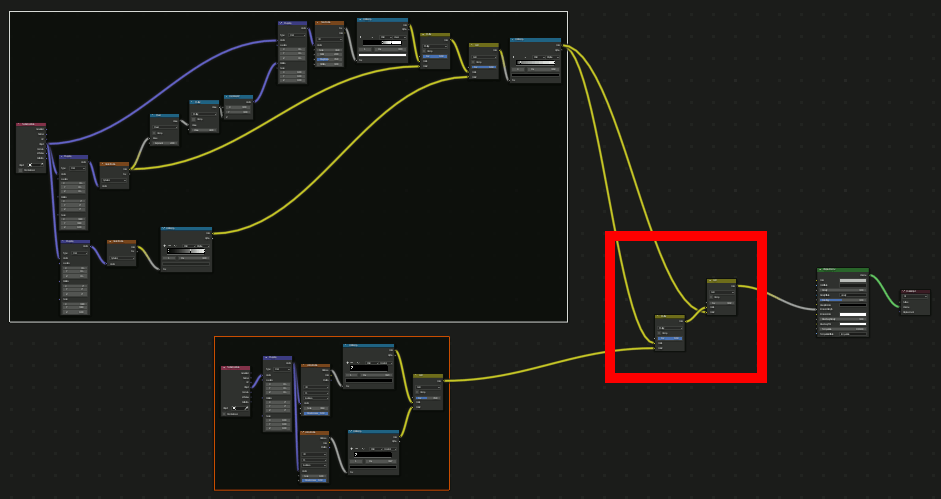
さらに、星雲にノイズを加えてよりそれらしくする
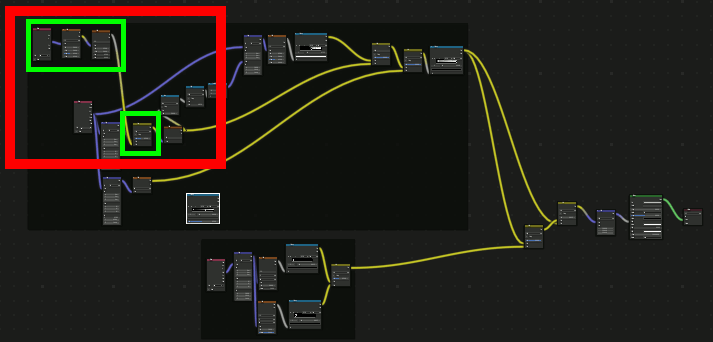
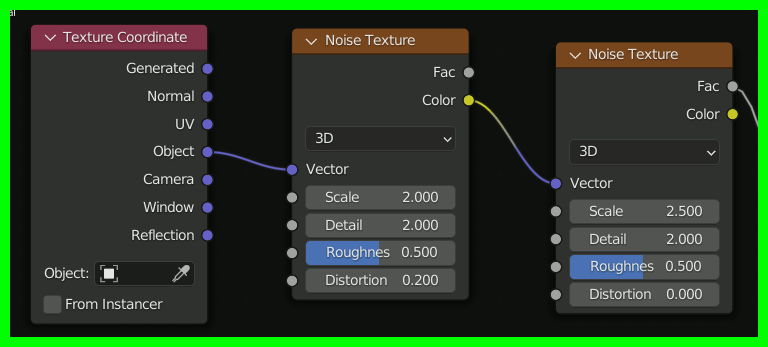

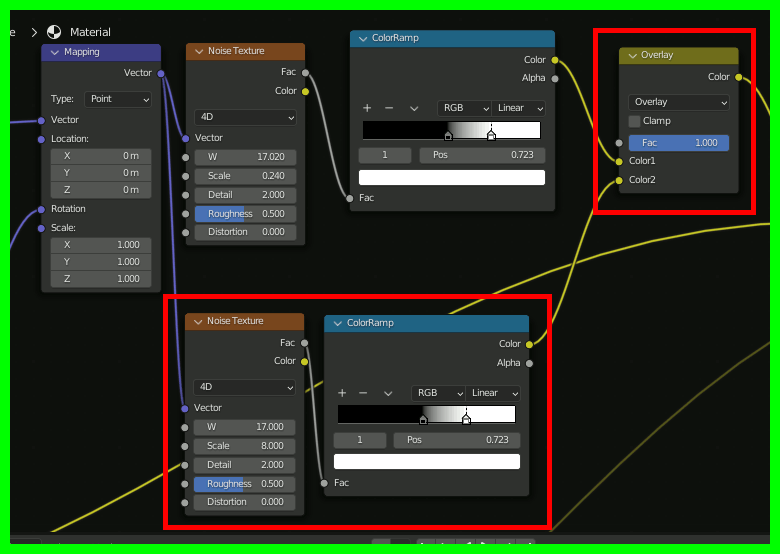
着色
結果
いろいろと調整して以下のように出来上がる。
Create a Galaxy in Blender – Iridesiumを試す(1)
https://www.youtube.com/watch?v=HCBW4fNAjBg
try-blender-tutorial-Create-a-Galaxy-in-Blender-Iridesium-2
Create a Galaxy in Blender – Iridesiumを試す(2)
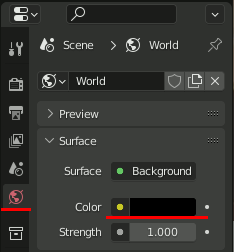
最初に背景を黒にしておく。
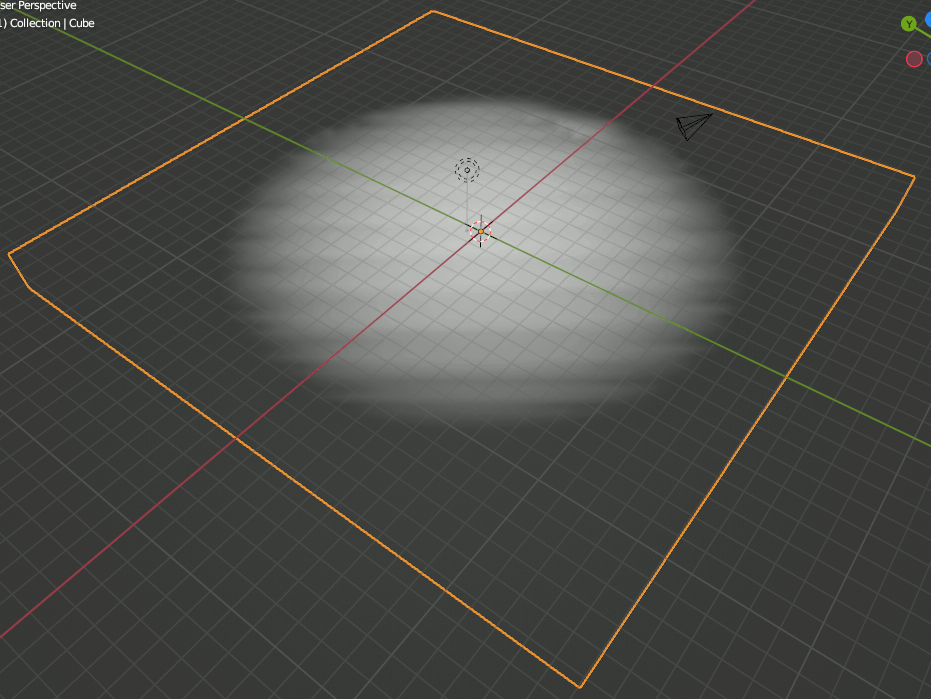
次にCubeを追加。座標系をObjectにするのでX,Y方向にやや大きめのSphereを追加する。
ここでは30x30x2の直方体とする。
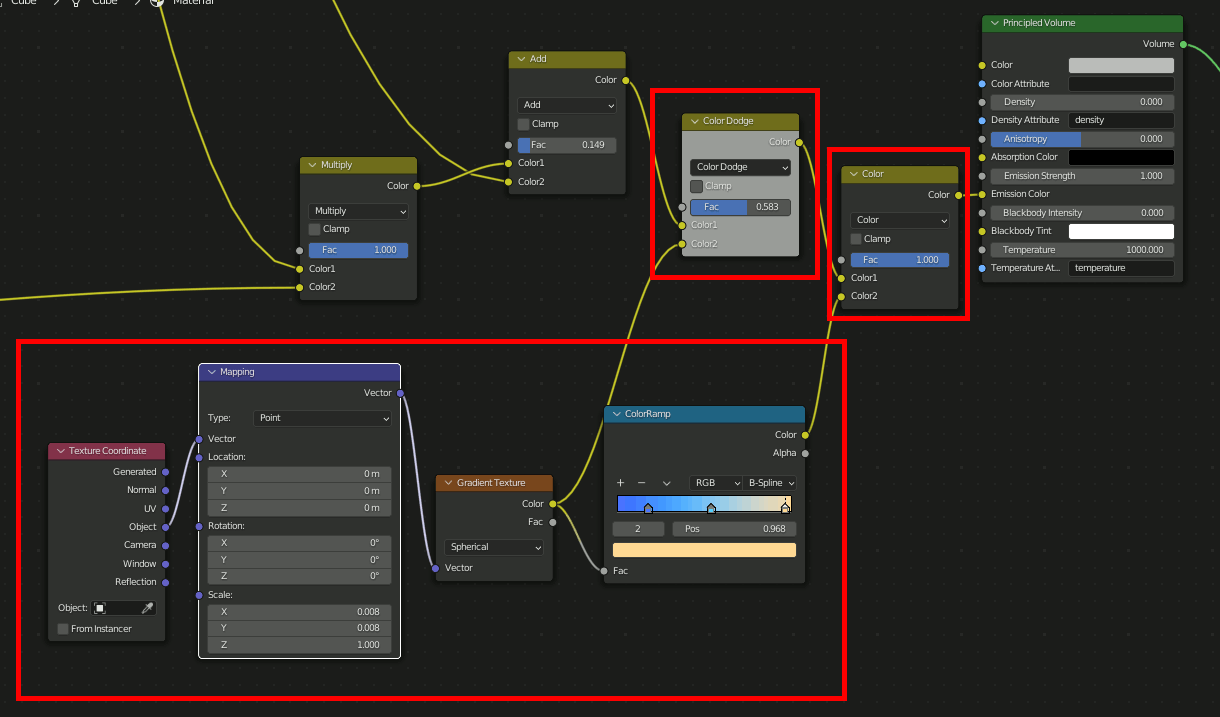
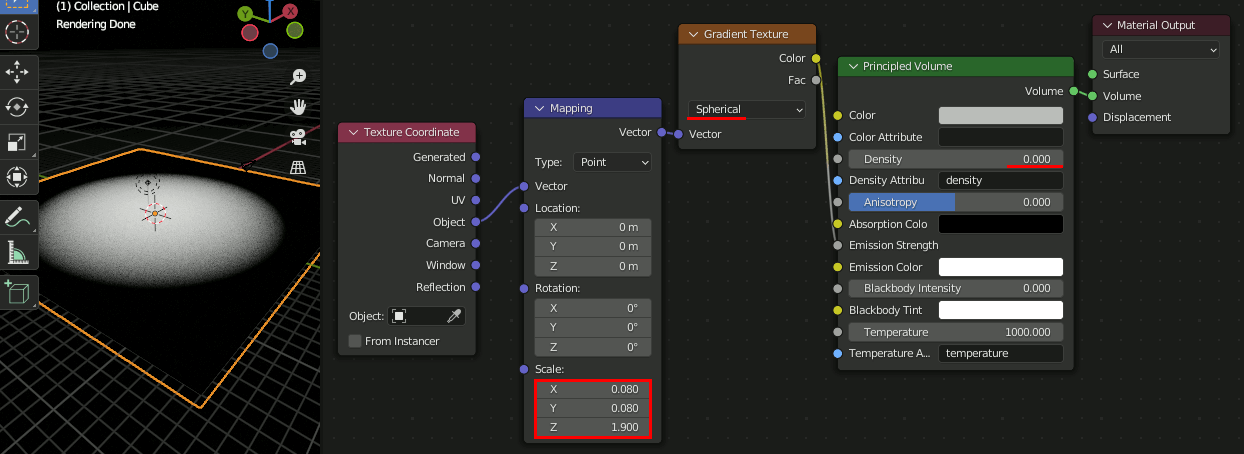
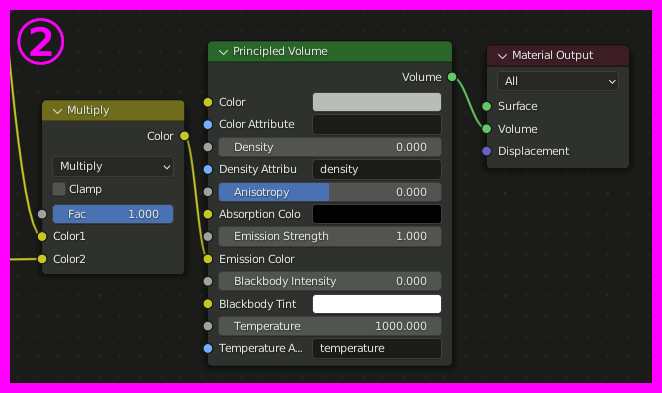
CubeにVolumeを追加し以下のように設定。
注:図ではPrincipled VolumeのEmission StrengthにつながっているがEmission Colorが正しい。
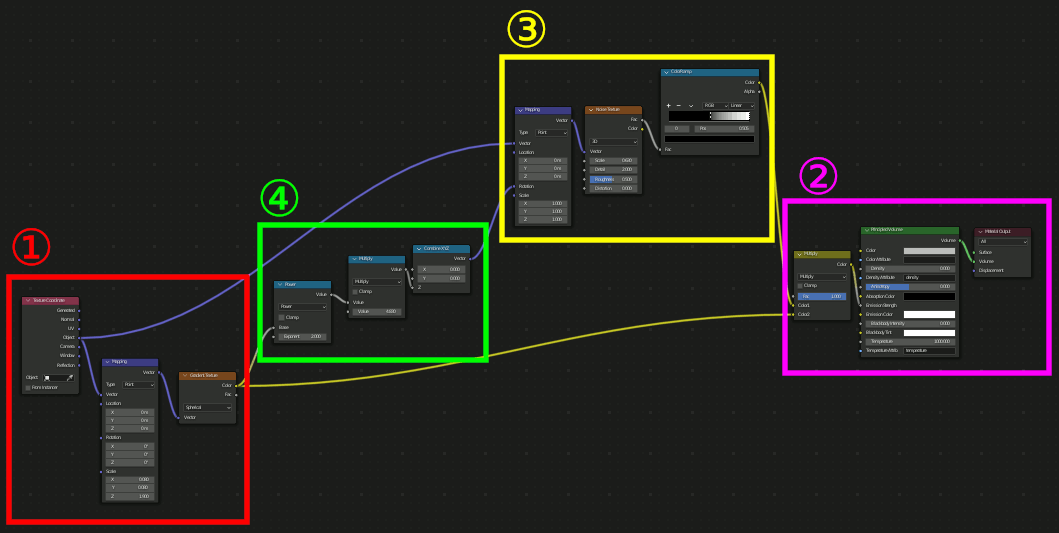
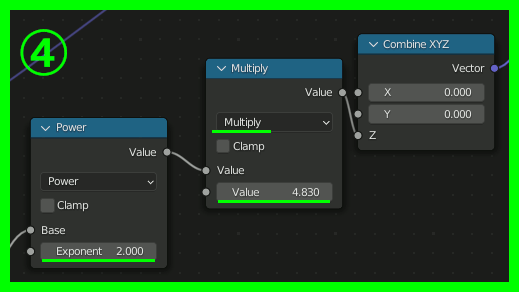
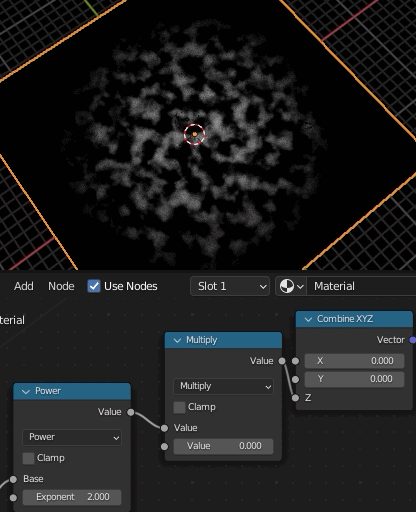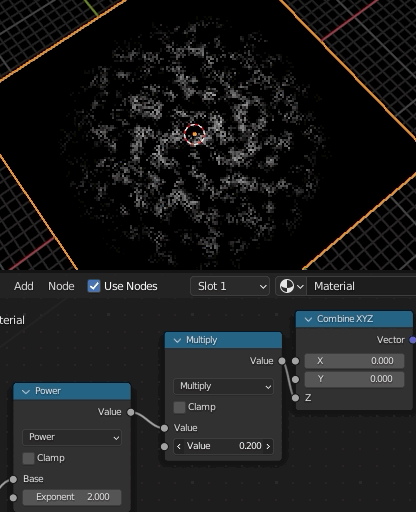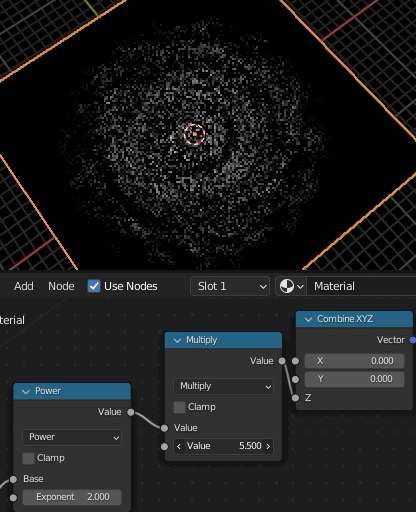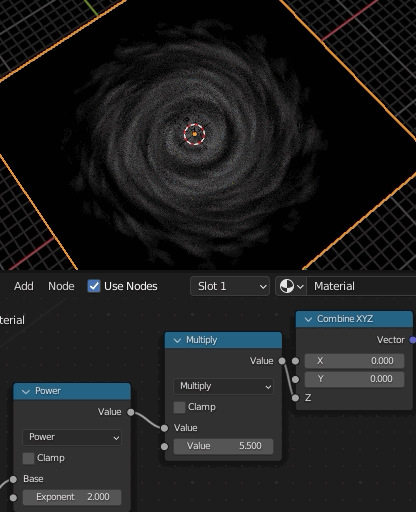
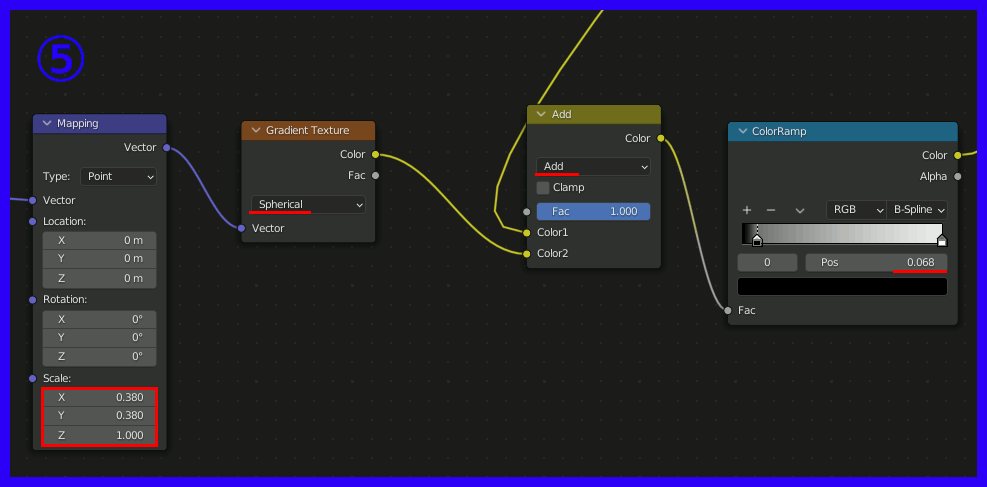
④、ここが最も重要な場所で、Gradient TextureのSpherical(=球状のグラデーション)をMappingのRotationに接続する。これによって中央から外側にかけて回転量を変化させ渦巻状を作成する。渦巻の巻き具合はGradient Textureの値に対するMathで調節する。
ここまでが基本的なアイデアとのこと。
続く。
glTexImage2D internalformat vs format
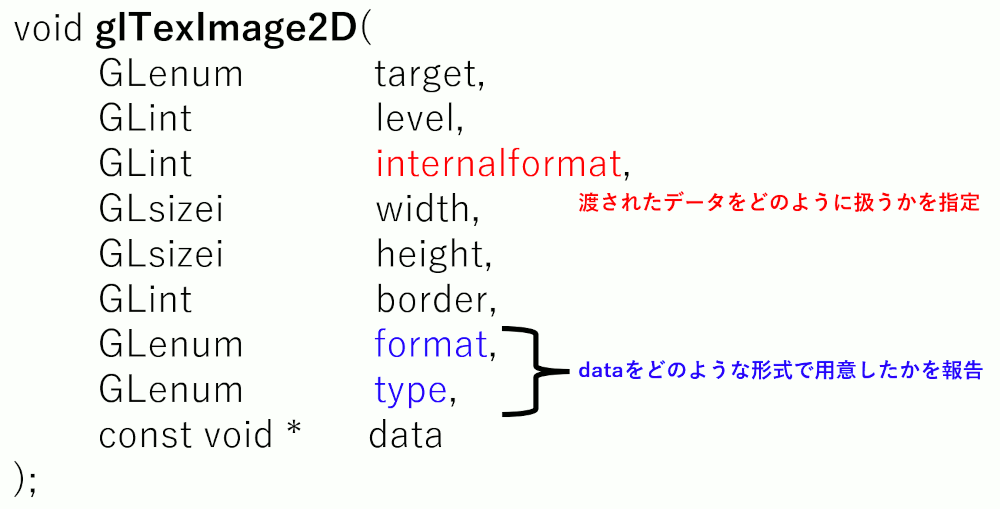
format,typeはテクスチャとして用意したメモリの形式。
internalformatはそれをOpenGLがどのように使うかを指定する。
#include <iostream> #include <array> #include <Windows.h> // GL_BGRなどを使うにはglew.hが必要。自分で定義してもいい #include <GL/glew.h> #include <gl/GL.h> #include <gl/GLU.h> #include <gl/freeglut.h> GLuint texName; //ウィンドウの幅と高さ int width, height; //描画関数 void disp(void) { glViewport(0, 0, width, height); glClearColor(0.2, 0.2, 0.2, 1); glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); //glEnable(GL_CULL_FACE); double v = 0.7; glEnable(GL_TEXTURE_2D); glBindTexture(GL_TEXTURE_2D, texName); glBegin(GL_QUADS); glTexCoord2f(0, 0); glVertex2f(-0.9, -0.9); glTexCoord2f(0, 1); glVertex2f(-0.9, 0.9); glTexCoord2f(1, 1); glVertex2f(0.9, 0.9); glTexCoord2f(1, 0); glVertex2f(0.9, -0.9); glEnd(); glFlush(); } //ウィンドウサイズの変化時に呼び出される void reshape(int w, int h) { width = w; height = h; disp(); } //エントリポイント int main(int argc, char** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(500, 500); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("sample"); glutDisplayFunc(disp); glutReshapeFunc(reshape); glEnable(GL_TEXTURE_2D); glGenTextures(1, &texName); glBindTexture(GL_TEXTURE_2D, texName); glPixelStorei(GL_UNPACK_ALIGNMENT, 1); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST); const int TEXSIZE = 2; std::array<unsigned char, 3> texrgb[TEXSIZE * TEXSIZE]; texrgb[0] = std::array<unsigned char, 3>{255, 0, 0 }; texrgb[1] = std::array<unsigned char, 3>{ 0, 255, 0 }; texrgb[2] = std::array<unsigned char, 3>{ 0, 0, 255}; texrgb[3] = std::array<unsigned char, 3>{255, 128, 0}; #if 0 // formatをGL_RGBにした場合 glTexImage2D( GL_TEXTURE_2D, 0, GL_RGB, // internalformat TEXSIZE, TEXSIZE,0, GL_RGB, // format GL_UNSIGNED_BYTE, &texrgb[0] ); #else // formatをGL_BGRにした場合 glTexImage2D( GL_TEXTURE_2D, 0, GL_RGB, // internalformat TEXSIZE, TEXSIZE,0, GL_BGR, // format GL_UNSIGNED_BYTE, &texrgb[0] ); #endif glutMainLoop(); return 0; }
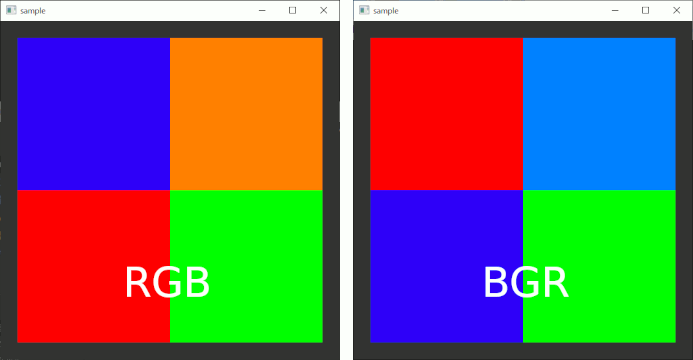
上の例では、例えば{255,0,0}というデータを用意する。これをformatで「RGBの順にデータが並んでいますよ」と指定すると、internalformatで「RGBのテクスチャを使う」と指定してあるので、赤いドットとなる。
逆に、「BGRの順にデータが並んでいますよ」と指定すると、internalformatで「RGBのテクスチャを使う」と指定してあるので、BGRの順にデータが並んでいることを考慮し、青いドットとなる。
このように、「formatでデータの並び方を確認し、internalformatで指定した解釈でテクスチャとして利用する」ので、「formatで指定した形式からinternalformatで指定した形式に変換されている」といえる。
厄介なのがほとんどの場合この変換をしてくれないので、実質組み合わせが決まっているようなものになっている。
PCLのpcl::getMeanStdDevは不偏標準偏差を返す
まず以下のプログラムを実行する。
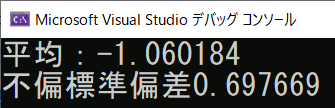
#include <iostream> #include <pcl/common/impl/common.hpp> //getMeanStdDev #pragma comment(lib,"pcl_commond.lib") int main() { std::vector<float> v; v.push_back(-1.841658711); v.push_back(-1.449076772); v.push_back(-1.04681015); v.push_back(-0.646572888); v.push_back(-0.25920701); v.push_back(0.149769783); v.push_back(-1.883069754); v.push_back(-1.481496215); v.push_back(-1.083532453); //不偏標準偏差 double mean, stddev; pcl::getMeanStdDev(v, mean, stddev); printf("平均:%lf\n", mean); printf("不偏標準偏差%lf\n", stddev); }
Excelで確認
Excelでは、母標準偏差(nで割る方)をSTDEV.P、不偏標準偏差(n-1で割る方)をSTDEV.Sで計算する。
母標準偏差と不偏標準偏差の違いは、母標準偏差は母集団に対して使うのに対して、不偏標準偏差は母集団の標本、つまり元データをサンプリングしたデータに対して使う。
ガウシアンフィルタについて(2)実装
#include <iostream> #include <vector> #include "ppmP3_read.hpp"
class Filter { //画像フィルタ std::vector< std::vector<float> > m_filter; public: //! @brief コンストラクタ //! @param [in] カーネルの一辺のサイズ Filter(const int size) { m_filter.resize(size, std::vector<float>(size, 0)); } //! @brief フィルタの数値を設定する関数 //! @param [in] row 行番号 //! @param [in] 一行分のデータ //! @return なし void set(int row, std::initializer_list<float> values) { int i = 0; for (auto v : values) { m_filter[row][i] = v; i++; } } //! @brief フィルタの全ての要素を割り算する //! @param [in] f 割る数 void operator/=(const float f) { for (auto&& row : m_filter) { for (auto&& c : row) { c /= f; } } } //! @brief フィルタのカーネルの一辺のサイズ int size() const{ return m_filter.size(); } //! @brief フィルタの要素を取得 //! @param [in] x -size()/2 から size()/2 までの整数 //! @param [in] y -size()/2 から size()/2 までの整数 float get(int x, int y)const { int sz = size() / 2; return m_filter[x + sz][y + sz]; } int posmin()const { return -size() / 2; } int posmax()const { return size() / 2; } };
struct image { unsigned char* src; int width; int height; int pixelsize; };
//! @brief 画像にフィルタを適用 //! @param [in] filter 画像フィルタ //! @param [in] x フィルタを適用する画素の座標 //! @param [in] y フィルタを適用する画素の座標 //! @param [in] src 元画像 //! @param [in] ret 結果画像 void apply(const Filter& filter,int x, int y,const image& src, unsigned char* ret) { const int posmin = filter.posmin(); const int posmax = filter.posmax(); const int pixSize = src.pixelsize; unsigned char* retp= &ret[pixSize * (y * src.width + x)]; for (int i = 0; i < pixSize; i++) { retp[i] = 0; } for (int fx = posmin; fx <= posmax; fx++) { for (int fy = posmin; fy <= posmax; fy++) { float g = filter.get(fx, fy); int yy = y + fy; int xx = x + fx; if (yy < 0 || xx < 0) continue; unsigned char* s = &src.src[pixSize * (yy * src.width + xx)]; for (int i = 0; i < pixSize; i++) { retp[i] += s[i]*g; } } } }
int main() { int width; int height; int vmax; // 画像を読み込む unsigned char * img_src = ppmP3_read( "C:\\dev\\c.ppm", &width, &height, &vmax, [](const size_t count) {return new unsigned char[count]; } ); std::vector<unsigned char> img_dst(width * height * 3); #define F1 //フィルタ作成 #ifdef F0 Filter ff(3); ff.set(0, { 1,2,1 }); ff.set(1, { 2,4,2 }); ff.set(2, { 1,2,1 }); ff /= 16.f; #elif defined(F1) Filter ff(5); ff.set(0, { 1, 4, 6, 4,1 }); ff.set(1, { 4,16,24,16,4 }); ff.set(2, { 6,24,36,24,6 }); ff.set(3, { 4,16,24,16,4 }); ff.set(4, { 1, 4, 6, 4,1 }); ff /= 256.f; #elif defined(F2) Filter ff(7); ff.set(0, { 1, 6, 15, 20, 15, 6, 1 }); ff.set(1, { 6, 36, 90,120, 90, 36, 6 }); ff.set(2, { 15, 90,225,300,225, 90, 15 }); ff.set(3, { 20,120,300,400,300,120, 20 }); ff.set(4, { 15, 90,225,300,225, 90, 15 }); ff.set(5, { 6, 36, 90,120, 90, 36, 6 }); ff.set(6, { 1, 6, 15, 20, 15, 6, 1 }); ff /= 4096.f; #endif //全てのピクセルにフィルタを適用 for (size_t x = 0; x < width; x++) { for (size_t y = 0; y < height; y++) { apply(ff,x, y, image{ img_src, width,height,3 }, img_dst.data()); } } //フィルタをかけた画像を保存 pnmP3_Write("C:\\dev\\e.ppm", 255, width, height, img_dst.data()); delete[]img_src; }
ガウシアンフィルタについて(1)
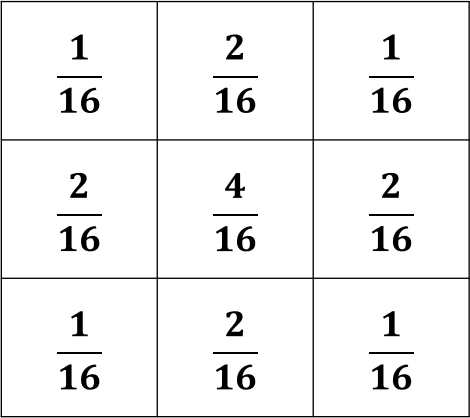
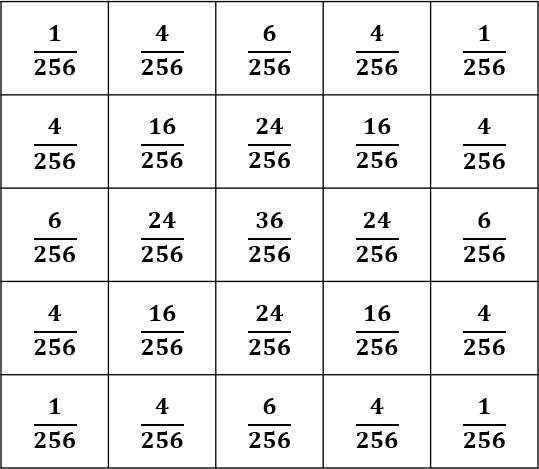
二次元画像のぼかしフィルタのガウシアンフィルタについて。検索すると3x3のフィルタとして以下が出てくる。
それとは別に以下の式が出てくる。
この式でどんな数字が出来上がるのかが気になったのでExcelで計算してみる。
Excelを開き、C5→I1に式を張り付ける。例えばC6の式は以下のようになる。
=(1/(2*PI()*$B$2*$B$2))*EXP(-(C$4*C$4+$B6*$B6)/(2*$B$2*$B$2))
※B2にρ、B3に分母を入れておく。
3x3の場合
上図左で得られた結果は最終結果なので、分数にしたときに1/16,2/16,...になっているはずなので、16倍する。そのうえで四捨五入すると上図右の結果となる。
5x5の場合
上の結果は検索して出てくる下のような5x5のフィルタと違う。
結論、7x7くらいまでは検索してすぐ出てくるフィルタを直打ちして使う、より大きなフィルタや個性的なフィルタを使いたい場合は式から作成する
主成分分析(PCA)の前にデータを標準化する(Eigenライブラリ版)
C++のEigenライブラリで標準化までやってみる。本当はPCAもやりたいしEigenSolverを使えばいい事まではわかっているが結果の確認ができないので今はやらない。
#include <iostream> #include <vector> #include <Eigen/Dense> int main() { std::vector<std::array<float, 3> > cloud; cloud.push_back({ -1.841658711, 0.324050009, 1.041258931 }); cloud.push_back({-1.449076772, 0.431593835, 0.987673104 }); cloud.push_back({-1.04681015, 0.415599823, 1.049820662 }); cloud.push_back({-0.646572888, 0.42549479, 1.087714672 }); cloud.push_back({-0.25920701, 0.599574149, 0.971796691 }); cloud.push_back({0.149769783, 0.497985959, 1.114130974 }); cloud.push_back({-1.883069754, 0.6849733, 1.249212146 }); cloud.push_back({-1.481496215, 0.677821219, 1.303076267 }); cloud.push_back({-1.083532453, 0.716715276, 1.313803315 }); Eigen::MatrixXf mat(9,3); for (size_t i = 0; i < cloud.size();i++) { mat.row(i) << cloud[i][0] , cloud[i][1] , cloud[i][2]; } // センタリングしたデータを作成 Eigen::MatrixXf centered = mat.rowwise() - mat.colwise().mean(); std::cout << "---" << std::endl;
// センタリングされたデータに対して、列ごとに標準偏差を求め、各列の要素を標準偏差で割る for (int c = 0; c < 3; c++) { auto col = mat.col(c).array(); double std_dev = sqrt((col - col.mean()).square().sum() / col.size()); centered.col(c) /= std_dev; }
std::cout << std::endl << centered << std::endl;// 表示 std::cout << std::endl << std::endl; ////////////////////// // 分散共分散行列 Eigen::MatrixXf cov = (centered.adjoint() * centered) / double(centered.rows());
std::cout << cov << std::endl;// 表示 return 0; }
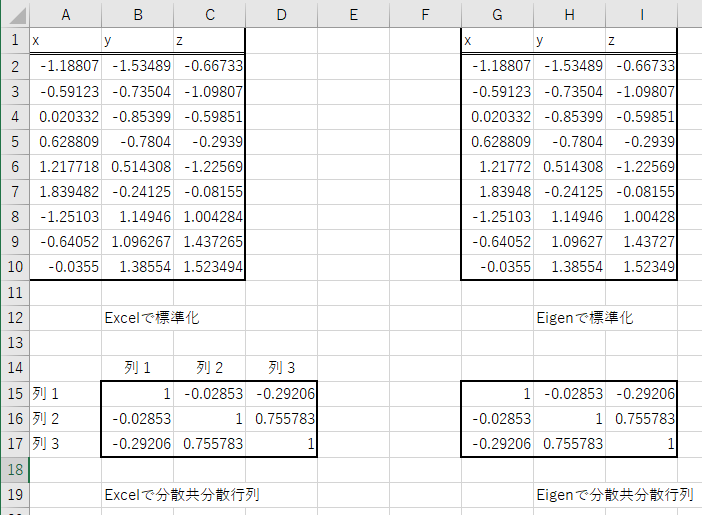
計算結果
Excelと同じ結果が出ている。
解説
センタリング
データのセンタリングは、データの平均値を0にすることなので、全てのデータから平均値を引けばよい。
rowwise()-colwise().mean()で行える。
// センタリングしたデータを作成 Eigen::MatrixXf centered = mat.rowwise() - mat.colwise().mean();
rowwise(),colwise()は全ての行に対して、あるいは全ての列に対して処理をしたい時に使う演算子みたいなもの。
例えばmean()は平均を計算する関数なので、colwise().mean()で各列の平均値を求めることができる
Eigen::MatrixXf mat(2, 3); mat.row(0) << 1, 3, 5; mat.row(1) << 2, 4, 6; std::cout << mat.colwise().mean() << std::endl;
結果:
つまり、各行の値に対して、これらを引けばよいので、
を呼び出す。
標準偏差
標準偏差は、全ての列のデータに対して、平均値を引いてそれを二乗したものを合計するわけだが、その計算をcolwise()で(なぜか)行えないので、一度arrayに変換する必要がある。
auto col = mat.col(c).array();
arrayに変換したら、arrayの各要素に対して演算を行える関数が用意されているので、それを駆使して列ごとに標準偏差を求める。
double std_dev = sqrt( (col/*各要素から*/ - col.mean()/*全要素の平均を引き*/) .square()/*それぞれ二乗して*/ .sum()/*全て合計して*/ / col.size()/*要素数で割り*/ )/*平方根をとる*/;
各列の要素を、標準偏差で割る。
centered.col(c) /= std_dev;
分散共分散行列
さっぱりわからん
おまけ PCA
主成分分析はEigenSolverに上記で計算した分散共分散行列のcovを入れて行うらしい。
//Eigen::SelfAdjointEigenSolver<Eigen::MatrixXf> es(cov); Eigen::EigenSolver<Eigen::MatrixXf> es(cov); Eigen::MatrixXcf eigen_vectors = es.eigenvectors(); Eigen::VectorXcf eigen_values = es.eigenvalues();
最後に
そもそもcovは分散共分散行列というヤツなのか?私は主成分分析をするにはそれにする必要があるらしいので、それに用いることができるならそれであろうという認識であって数学的な事は何一つ理解していないのだが。
主成分分析(PCA)の計算をする前にデータを標準化しないといけないらしい
厳密には、したほうがいい場合としないほうがいい場合があるらしい。
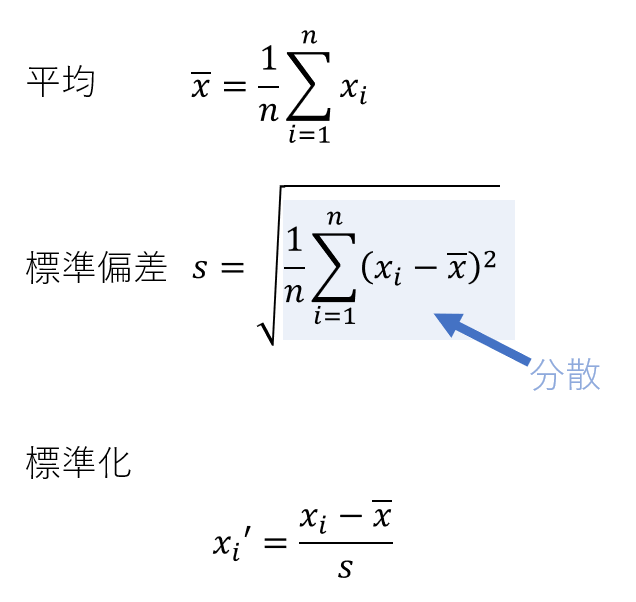
標準化の式は以下。各値から値全体の平均を引き、その値を標準偏差で割る。これをすべての値に対して行う。
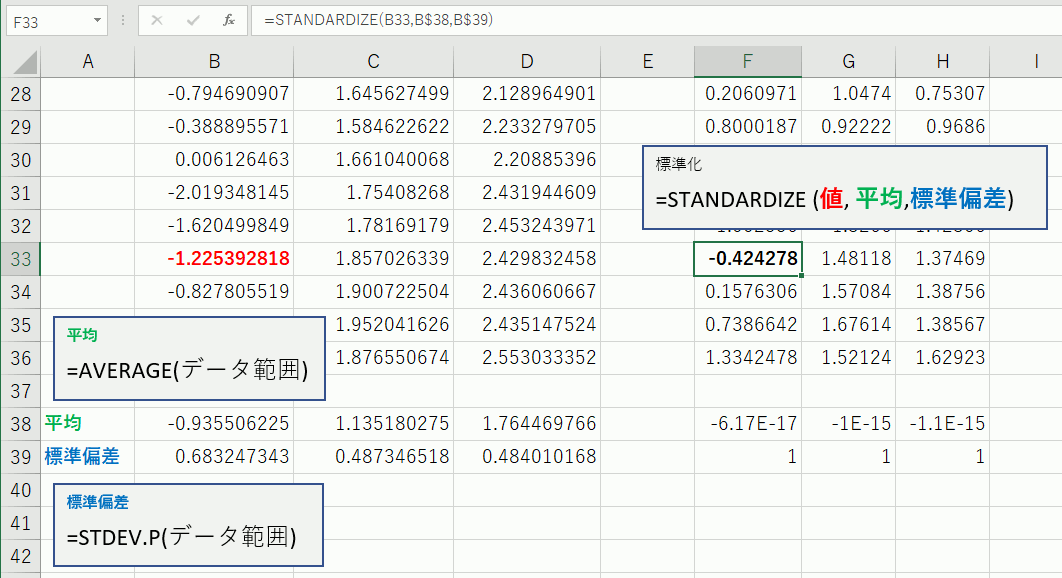
Excelで計算
エクセルにはSTANDARDIZEという関数がある。ただしこれを使うためには平均と標準偏差をそれぞれ別途計算する必要がある。
検証
自前実装したコードと上記Excelで半自動計算したものと比較。同じ値が出ている。
サンプルコード
#include <iostream> #include <vector> #include <array> using vector3f = std::vector<std::array<float, 3>>;
//! @brief データの平均を求める //! @param [in] vec データの配列 //! @return 各要素の平均 std::array<float, 3> Average(const vector3f& vec) { // 初期化 std::array<float, 3> ave; ave[0] = 0; ave[1] = 0; ave[2] = 0; // 各要素平均 for (size_t i = 0; i < vec.size(); i++) { ave[0] += vec[i][0]; ave[1] += vec[i][1]; ave[2] += vec[i][2]; } ave[0] /= vec.size(); ave[1] /= vec.size(); ave[2] /= vec.size(); return ave; }
//分散 std::array<float, 3> Distributed(const std::array<float, 3>& average, const vector3f& vec) { int n = vec.size(); std::array<float, 3> s2{ 0,0,0 }; for (int j = 0; j < 3; j++) { for (const auto& v : vec) { s2[j] += std::pow(v[j] - average[j], 2); } s2[j] = 1.f / n * s2[j]; } return s2; }
//標準偏差 std::array<float, 3> StandardDeviation(const std::array<float, 3>& average, const vector3f& vec) { std::array<float, 3> d = Distributed(average, vec); d[0] = sqrt(d[0]); d[1] = sqrt(d[1]); d[2] = sqrt(d[2]); return d; }
//標準化 平均を引いて標準偏差で割る // average 平均 // sd 標準偏差 void Standardization(vector3f& src, const std::array<float, 3>& average, const std::array<float, 3>& sd) { for (auto&& p : src) { p[0] = (p[0] - average[0]) / sd[0]; p[1] = (p[1] - average[1]) / sd[1]; p[2] = (p[2] - average[2]) / sd[2]; } }
int main() { vector3f data; data.push_back({ -1.841658711,0.324050009,1.041258931 }); data.push_back({-1.449076772,0.431593835,0.987673104 }); data.push_back({-1.04681015,0.415599823,1.049820662 }); data.push_back({-0.646572888,0.42549479,1.087714672 }); data.push_back({-0.25920701,0.599574149,0.971796691 }); data.push_back({ 0.149769783,0.497985959,1.114130974 }); data.push_back({-1.883069754,0.6849733,1.249212146 }); data.push_back({-1.481496215,0.677821219,1.303076267 }); data.push_back({-1.083532453,0.716715276,1.313803315 }); std::array<float, 3> _s = Average(data); std::array<float, 3> sd = StandardDeviation(_s, data); Standardization(data, _s, sd); for (size_t i = 0; i < data.size(); i++) { printf("%lf , %lf , %lf\n", data[i][0], data[i][1], data[i][2]); } }