Blender Cycles White Noise Texture
いつの間にかCyclesにWhite Noise Textureが入っていた。確認しているバージョンは2.83,2.90。確か2.7系には無かった気がする。Blender Renderが廃止された?時に移行があったのかもしれない。
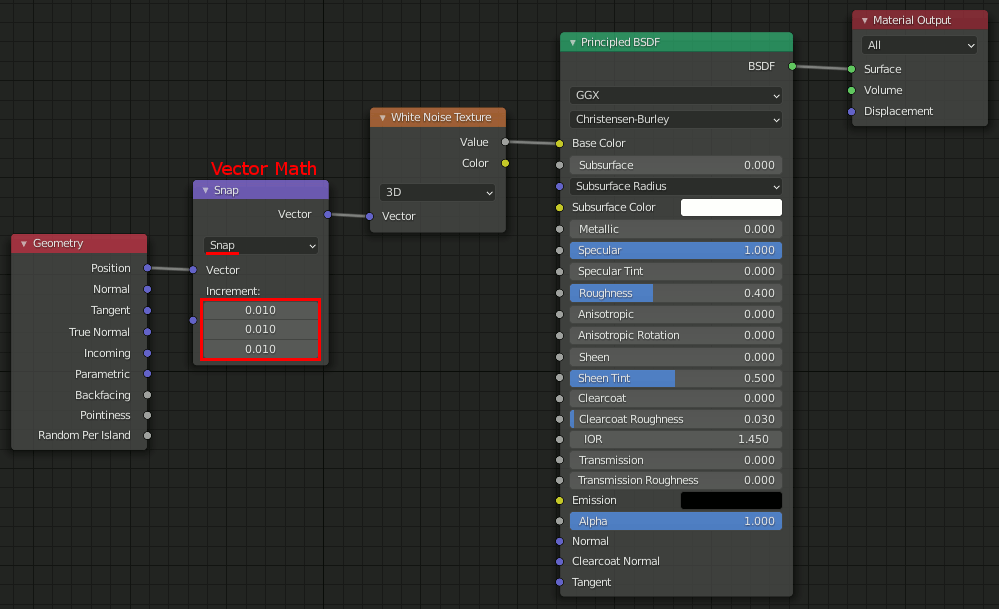
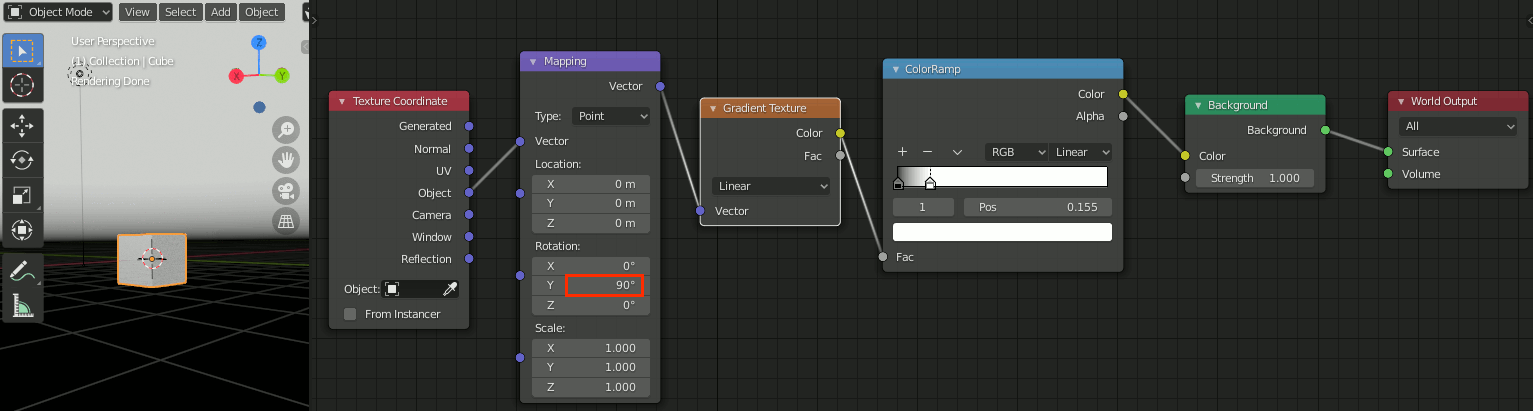
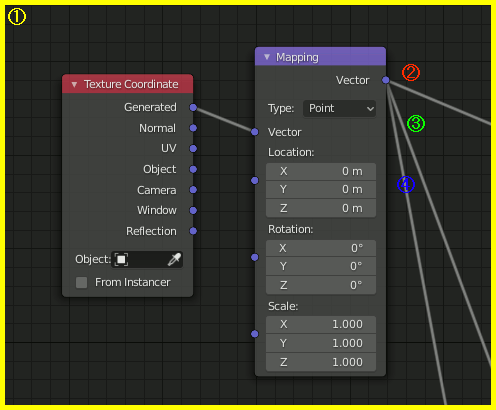
基本的なノード接続
応用
そのままだとあまりにもわかりにくいので、vector mathでsnapを設定する。
Blender のSky Textureを半球にする
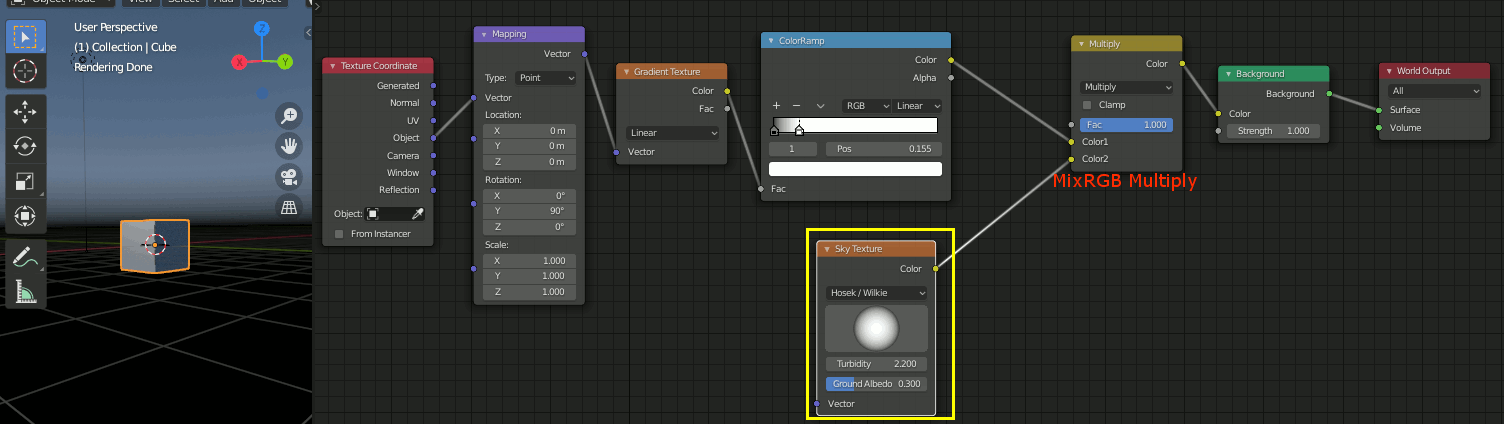
SkyTextureは便利だが水平面より下にも色がついている。これを編集し水平面には色がつかないようにする。
Worldで以下のようにノードを設定する。
そしてSkyTextureとMixRGBでMultiplyする
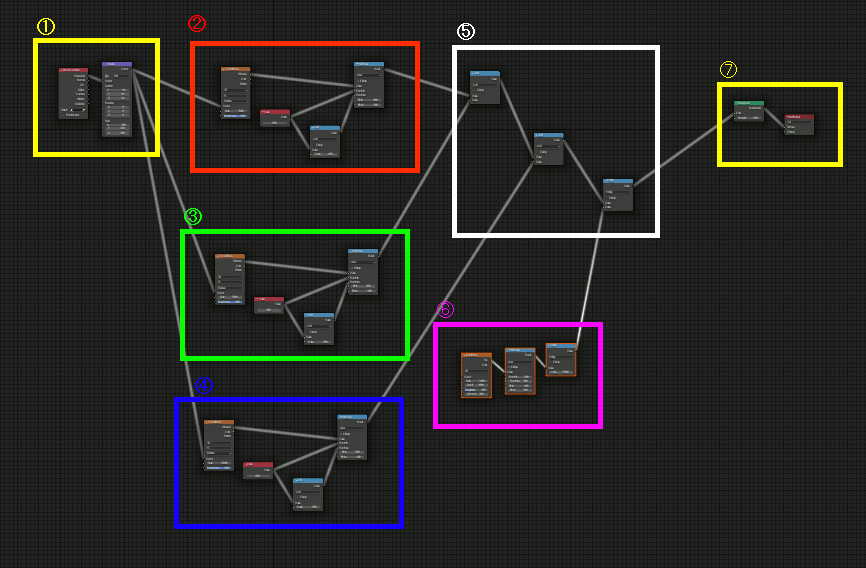
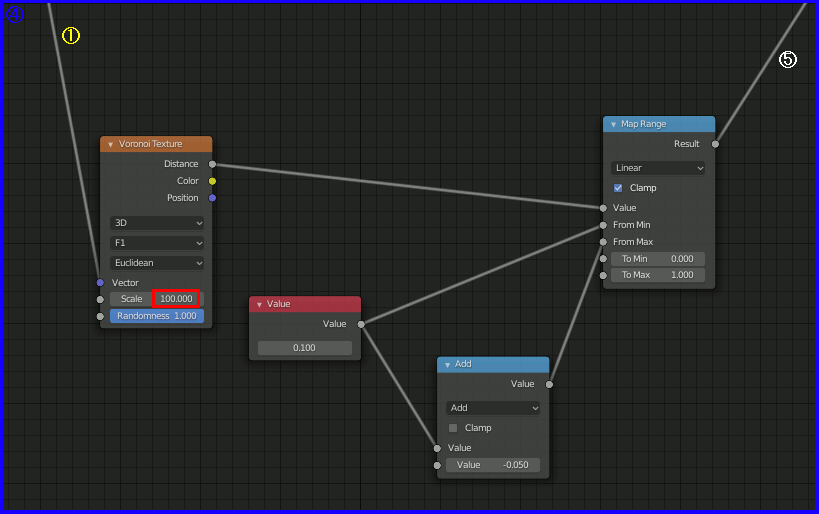
応用で、空の部分だけを星空にする。

Make a Procedural Starry Sky HDRI with Nodes | Blender 2.82 のチュートリアルを試す
星空のチュートリアルで比較的短い物。
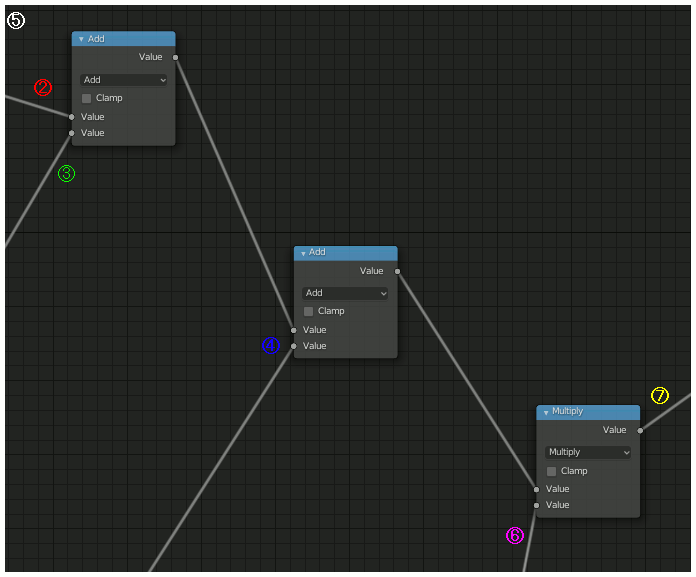
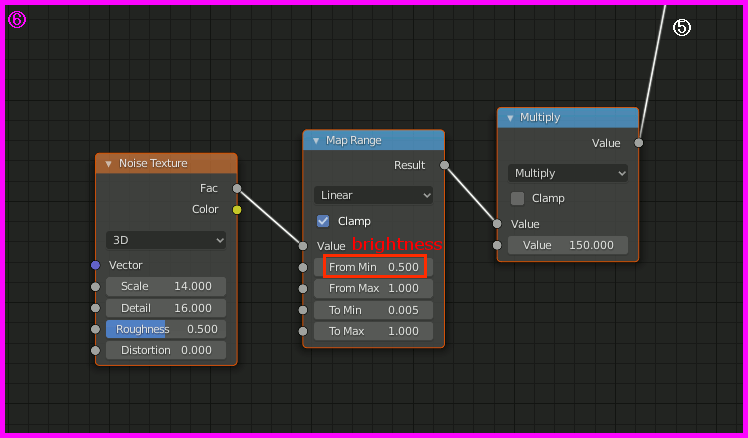
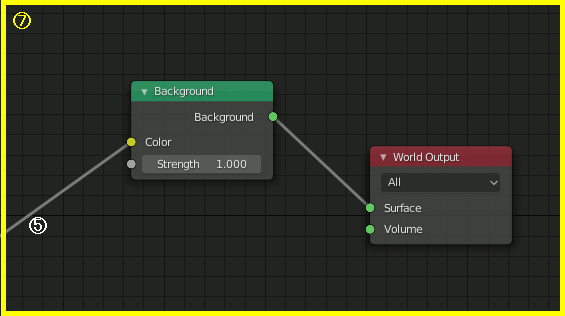
ざっくりいうとBackgroundを以下のノードで設定する。
⑥のFrom Minを0に近づけると明るくなる。
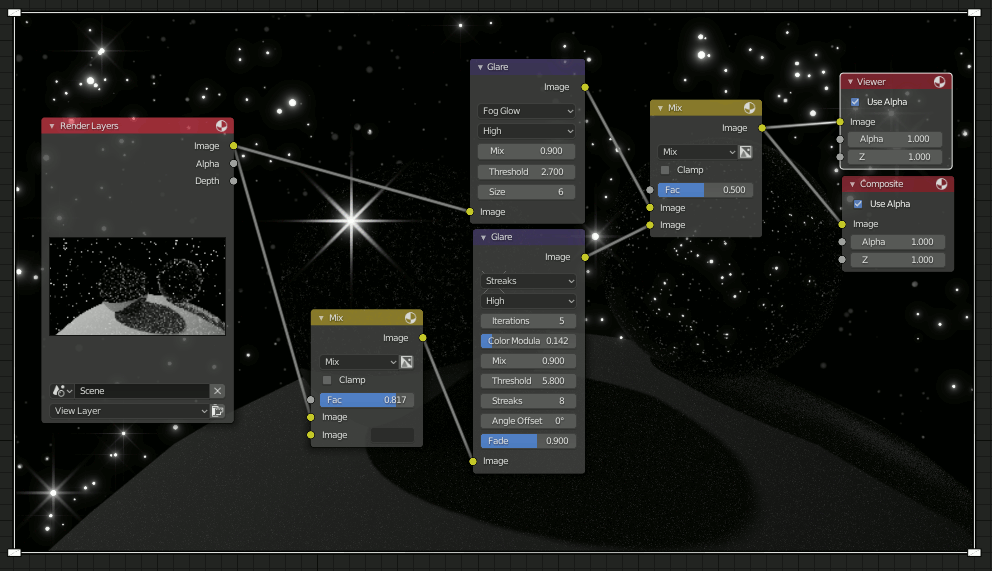
EEVEEの場合レンダリング結果に直接Bloomがかかるのでわかりやすいが、Cyclesの場合は後からcompositorで設定しなければならない。
CyclesでのBloomの設定
compositorで設定する。
色々と加工してみた例。
unsigned charにビット単位でアクセスするクラス
1bit単位の処理が必要になったので、charの各ビットに[]でアクセスできるクラスを書いた。
今見たら、クラス名iteratorはおかしい。まあいいか。
プログラム本体
#include <iostream> #include <bitset>
//! @brief 1ビットにoperator=を提供するためのクラス class bititerator_t { unsigned char* m_c; int m_index; public: bititerator_t(unsigned char* c, const int index) { m_c = c; m_index = 7-index; } void operator=(const int value) { unsigned char mask = (1 << m_index); if (value) { *m_c |= mask; } else { *m_c &= ~mask; } } operator unsigned char() { unsigned char mask = (1 << m_index); return (*m_c & mask) ? 1 : 0; } };
//! @brief ビットを配列のようにアクセスするクラス class BitArray { unsigned char c; public: BitArray() :c(0) {} //! @brief 各ビットへ[]でアクセスする bititerator_t operator[](const int i) { return bititerator_t(&c, i); } operator unsigned char(){ return c; } //内部のunsigned charデータへ書き込む unsigned char operator=(const unsigned char value) { c = value; return c; } };
int main() { BitArray bit; bit[0] = 1; bit[1] = 0; bit[2] = 1; bit[3] = 1; bit[4] = 0; bit[5] = 0; bit[6] = 0; bit[7] = 0; std::cout << (unsigned int)bit << " " << std::bitset<8>(bit) << std::endl; int i; std::cin >> i; }
結果
176 10110000
GLSLを試す (8) Index Buffer Object
この図では三角形を2枚書いて、IBOを使わない場合、定義しなければいけない頂点数は6となる。
IBOを使うと共通に使用する頂点をまとめて4個にできる。
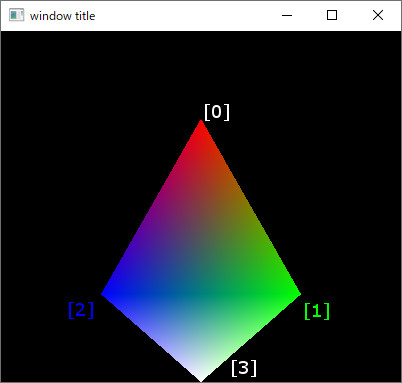
基本は以下と同じ:
GLSLを試す (1)
注目すべき点は、
・頂点バッファの定義は普通と同じ形式で良い
・IBOを使うからと言って、バーテクスシェーダ、フラグメントシェーダに変更を加える必要は無い
・頂点バッファなどを準備する時に、一緒にGL_ELEMENT_ARRAY_BUFFERでIBOを作成する
・glDrawArraysではなくglDrawElementsを使用する
バッファの準備
// バッファとデータ typedef GLfloat points_t[3]; GLuint vertexbuffer;//バッファのIDを格納する変数 GLuint colorbuffer;//バッファのIDを格納する変数 GLuint indexbuffer;//三角形を頂点IDで表現するバッファのIDを格納する変数 //////////////////////////////////////////////////
// データの準備
void prepare_buffers() { points_t position[4]; points_t color[4]; //頂点座標 position[0][0] = 0; position[0][1] = 0.5; position[0][2] = 0; position[1][0] = 0.5; position[1][1] = -0.5; position[1][2] = 0; position[2][0] = -0.5; position[2][1] = -0.5; position[2][2] = 0; position[3][0] = 0; position[3][1] = -1.0; position[3][2] = 0; //色 color[0][0] = 1.0; color[0][1] = 0.0; color[0][2] = 0.0; color[1][0] = 0.0; color[1][1] = 1.0; color[1][2] = 0.0; color[2][0] = 0.0; color[2][1] = 0.0; color[2][2] = 1.0; color[3][0] = 1.0; color[3][1] = 1.0; color[3][2] = 1.0; //頂点座標のバッファ glGenBuffers(1, &vertexbuffer); glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer); glBufferData( GL_ARRAY_BUFFER, 4 * 3 * sizeof(GLfloat), position, GL_STATIC_DRAW); //頂点カラーのバッファ glGenBuffers(1, &colorbuffer); glBindBuffer(GL_ARRAY_BUFFER, colorbuffer); glBufferData( GL_ARRAY_BUFFER, 4 * 3 * sizeof(GLfloat), color, GL_STATIC_DRAW);
//頂点Indexで表現した三角形一覧 // △012,△213 の二つを定義 GLuint triangle_elements[] = { 0,1,2 , 2,1,3 }; //三角形の頂点IDのバッファ const size_t triangle_elements_memsize = sizeof(triangle_elements);
glGenBuffers(1, &indexbuffer); glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, indexbuffer); glBufferData( GL_ELEMENT_ARRAY_BUFFER, triangle_elements_memsize, // バッファのメモリ上のバイト数を求める triangle_elements, //バッファへのポインタ GL_STATIC_DRAW ); glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, 0);
}
レンダリング
void display(void) { glClearColor(0, 0, 0, 1); glClear(GL_COLOR_BUFFER_BIT); // シェーダを使う glUseProgram(ProgramID); // 頂点バッファ:頂点 glEnableVertexAttribArray(0); glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer); glVertexAttribPointer( 0, // シェーダ内のlayoutとあわせる 3, // 1要素の要素数(x,y,z)で3要素 GL_FLOAT, // タイプ GL_FALSE, // 正規化しない(データが整数型の時) 0, // ストライド (void*)0 // 配列バッファオフセット ); // カラーバッファを有効にする glEnableVertexAttribArray(1); glBindBuffer(GL_ARRAY_BUFFER, colorbuffer); glVertexAttribPointer( 1, // シェーダ内のlayoutとあわせる 3, // 1要素の要素数(r,g,b)で3要素 GL_FLOAT, // タイプ GL_FALSE, // 正規化しない(データが整数型の時) 0, // ストライド (void*)0 // 配列バッファオフセット );
// 三角形を描きます! glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, indexbuffer); //int size; //glGetBufferParameteriv(GL_ELEMENT_ARRAY_BUFFER, GL_BUFFER_SIZE, &size); glDrawElements( GL_TRIANGLES, 6, // 頂点数。size / sizeof(GLuint) の式でも頂点数を算出できる。 GL_UNSIGNED_INT, 0 );
glDisableVertexAttribArray(0);//バッファを無効にする glDisableVertexAttribArray(1); glFlush(); }
シェーダー
各シェーダはIBOの使用の有無で書き換える必要は無い。
頂点シェーダ
#version 460 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 incolor; out vec4 vertexColor; void main() { gl_Position = vec4(aPos, 1.0); vertexColor = vec4(incolor, 1.0); }
フラグメントシェーダ
#version 460 core out vec4 FragColor; in vec4 vertexColor; void main() { FragColor = vertexColor; }
√-2
Blender Pythonでxyz出力してC++で読み込む
Blender側
import bpy msh = bpy.context.active_object fname = 'C:/test/' + msh.name + '.xyz' with open(fname, 'w') as myf: for vt in msh.data.vertices: print(vt.co[0],vt.co[1],vt.co[2] ,file=myf ) #頂点座標出力
C++側
//! @brief separator区切りの実数の一覧を読み込む //! @details xyzフォーマットは正式な規格として存在しないらしいので、ある程度の柔軟性を持たせる //! @param [out] ret 結果を格納する配列の配列 //! @param [in] filename ファイル名 //! @param [in] separator 区切り文字 //! @return なし template<typename scalar_t> void read_xyz(std::vector<std::vector<scalar_t> >& ret,const char* filename, const char separator) { std::ifstream ifs(filename); std::string str; while (std::getline(ifs, str)) { std::stringstream line{ str }; std::string value; std::vector<scalar_t> tmp; while (getline(line, value, separator)){ tmp.push_back(std::atof(value.c_str())); } ret.push_back(tmp); } }
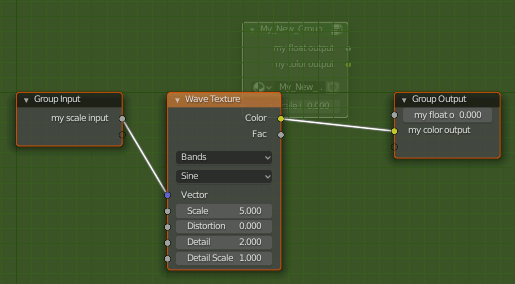
Blender python でCyclesにNode Groupを追加
ソースコード
import bpy tree = bpy.data.materials['Material'].node_tree def create_nodegroup(): # create node group my_new_Group = bpy.data.node_groups.new('My_New_Group', 'ShaderNodeTree') # input mngInputs = my_new_Group.nodes.new('NodeGroupInput') mngInputs.location = (0,0) my_new_Group.inputs.new('NodeSocketFloat','my scale input') # output mngOutputs = my_new_Group.nodes.new('NodeGroupOutput') mngOutputs.location = (500,0) my_new_Group.outputs.new('NodeSocketFloat','my float output') my_new_Group.outputs.new('NodeSocketColor','my color output') # node in nodegroup texnode = my_new_Group.nodes.new('ShaderNodeTexWave') texnode.location = (200,0) # connect nodes my_new_Group.links.new(mngInputs.outputs[0],texnode.inputs[0]) my_new_Group.links.new(texnode.outputs['Color'],mngOutputs.inputs['my color output']) return my_new_Group ################################################################ ###################### Add New Node Group ###################### ################################################################ groupnode = tree.nodes.new(type='ShaderNodeGroup') groupnode.node_tree = create_nodegroup()
結果
なおNode Groupから出るには[Tab]キーを押す
二次元の三角形の内外判定
http://www.thothchildren.com/chapter/5b267a436298160664e80763
上記サイトはC言語のサンプルが載っている今時珍しいサイトでお世話になっているのだが一カ所致命的なミスがある。コメントしたいがログイン式になっていてできないので代わりにここに書いておきたい。
以下、上記サイトのベクトルの係数による解法の修正版
template<typename real_t> inline bool isInTheTriangle( real_t px, real_t py, real_t p0x, real_t p0y, real_t p1x, real_t p1y, real_t p2x, real_t p2y ) { real_t Area = 0.5 * (-p1y * p2x + p0y * (-p1x + p2x) + p0x * (p1y - p2y) + p1x * p2y); real_t s = 1.0 / (2.0 * Area) * (p0y * p2x - p0x * p2y + (p2y - p0y) * px + (p0x - p2x) * py); real_t t = 1.0 / (2.0 * Area) * (p0x * p1y - p0y * p1x + (p0y - p1y) * px + (p1x - p0x) * py); if (
(0 < s) && (s < 1) && (0 < t) && (t < 1) && (0 < (1 - s - t)) && ((1 - s - t) < 1)
) { return true; } else { return false; } }
ついでにテンプレート化も施した。
C言語の比較演算子は左結合で、左から右に向かって零,非零の値に変換していく。従って 0 < a < b という形の比較ができない。必ず (0<a)&&(a<b)と書かなければいけない。めんどくさいがそうなのだ。
ちなみに外積を使ったやり方の方は問題ない。
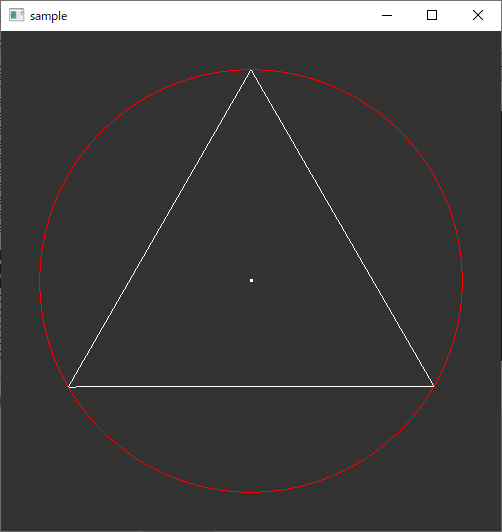
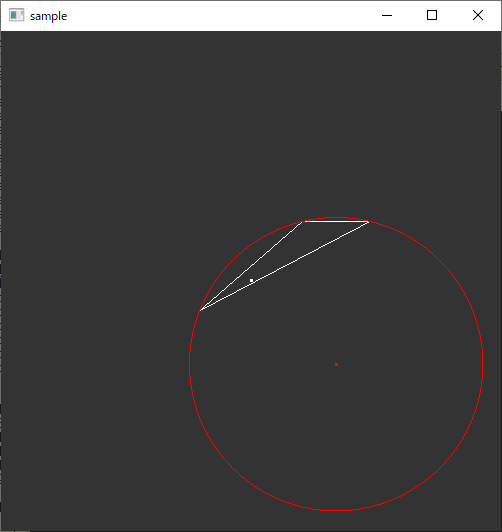
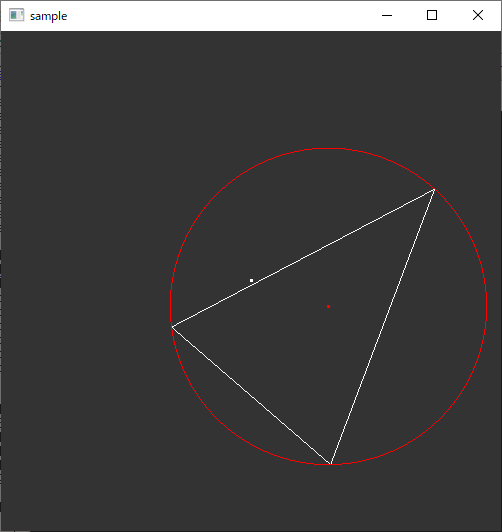
三角形の外接円を求める(二次元)
ソースコード
//! @brief 外接円を求める //! @param [out] x 外接円の中心のx座標 //! @param [out] y 外接円の中心のy座標 //! @param [out] r 外接円の半径 //! @param [in] x1 三角形の第一頂点のx座標 //! @param [in] y1 三角形の第一頂点のy座標 //! @param [in] x2 三角形の第二頂点のx座標 //! @param [in] y2 三角形の第二頂点のy座標 //! @param [in] x3 三角形の第三頂点のx座標 //! @param [in] y3 三角形の第三頂点のy座標 //! @return なし inline void Circumscribed_Circle( double* x, double* y, double* r, const double x1, const double y1, const double x2, const double y2, const double x3, const double y3 ) { double xT = (y3 - y1) * (x2 * x2 - x1 * x1 + y2 * y2 - y1 * y1) + (y1 - y2) * (x3 * x3 - x1 * x1 + y3 * y3 - y1 * y1); double yT = (x1 - x3) * (x2 * x2 - x1 * x1 + y2 * y2 - y1 * y1) + (x2 - x1) * (x3 * x3 - x1 * x1 + y3 * y3 - y1 * y1); double c = 2 * ((x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)); *x = xT / c; *y = yT / c; *r = sqrt( (*x - x1) * (*x - x1) + (*y - y1) * (*y - y1) ); }
実行例