月火水木金土日
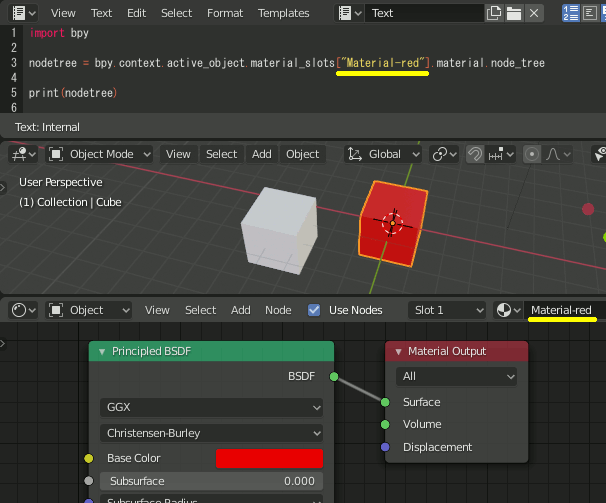
Blender Pythonからマテリアルのノードへアクセス（２）
ノードを追加
import bpy nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes nodes.new('ShaderNodeBsdfDiffuse')
ノードを削除
import bpy nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes nodes.remove( nodes['Diffuse BSDF'] )
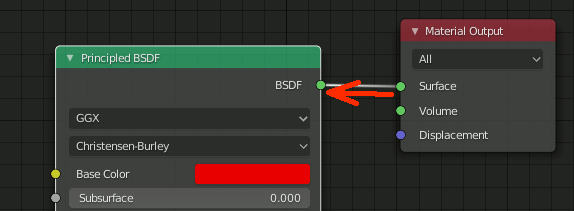
ノード同士を接続
import bpy nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes diffuse = nodes['Diffuse BSDF'] MaterialOutput = nodes['Material Output'] nodetree.links.new(diffuse.outputs[0],MaterialOutput.inputs[0])
ノードのラベルを変更
import bpy nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes diffuse = nodes['Diffuse BSDF'] diffuse.label = "Diffuse BSDF -added"
Blender Pythonからマテリアルのノードへアクセス（１）
マテリアルからノードツリーを取得
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree print(nodetree)
あるいは、以下でも可
nodetree = bpy.context.active_object.material_slots[0].material.node_tree
出力結果：
<bpy_struct, ShaderNodeTree("Shader Nodetree")>
ノードへアクセス
全てのノードを表示
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes for n in nodes: print(n)
出力結果：
<bpy_struct, ShaderNodeOutputMaterial("Material Output")>
<bpy_struct, ShaderNodeBsdfPrincipled("Principled BSDF")>
<bpy_struct, ShaderNodeBsdfPrincipled("Principled BSDF")>
ノードの入力を列挙
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes for i in nodes["Material Output"].inputs : print(i)
または：
print(nodes["Material Output"].inputs[0])
または：
print(nodes["Material Output"].inputs["Surface"])
出力結果：
<bpy_struct, NodeSocketShader("Surface")>
<bpy_struct, NodeSocketShader("Volume")>
<bpy_struct, NodeSocketVector("Displacement")>
<bpy_struct, NodeSocketShader("Volume")>
<bpy_struct, NodeSocketVector("Displacement")>
ノードの入力元を取得
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes print(nodes["Material Output"].inputs[0].links[0].from_node )
出力結果：
<bpy_struct, ShaderNodeBsdfPrincipled("Principled BSDF")>
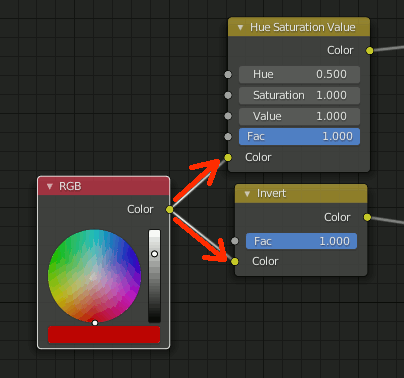
ノードの出力先を列挙
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes for n in nodes["RGB"].outputs[0].links : print(n.to_node)
または：
print(nodes["RGB"].outputs[0].links[0].to_node )
print(nodes["RGB"].outputs[0].links[1].to_node )
print(nodes["RGB"].outputs[0].links[1].to_node )
出力結果：
<bpy_struct, ShaderNodeHueSaturation("Hue Saturation Value")>
<bpy_struct, ShaderNodeInvert("Invert")>
<bpy_struct, ShaderNodeInvert("Invert")>
ノードの値を取得
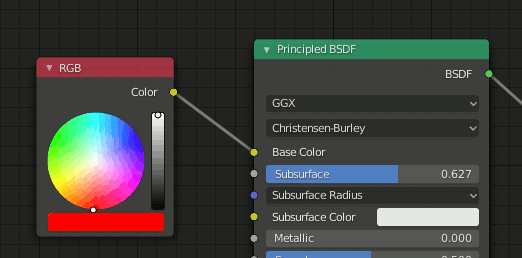
nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes print(nodes["RGB"].outputs[0].default_value[0]) print(nodes["RGB"].outputs[0].default_value[1]) print(nodes["RGB"].outputs[0].default_value[2])
出力結果
0.8000000715255737
0.0012105016503483057
0.0
0.0012105016503483057
0.0
import bpy nodetree = bpy.context.active_object.material_slots["Material-red"].material.node_tree nodes = nodetree.nodes print("Base Color ", nodes["Principled BSDF"].inputs["Base Color"].default_value[0]) print("Base Color ", nodes["Principled BSDF"].inputs["Base Color"].default_value[1]) print("Base Color ", nodes["Principled BSDF"].inputs["Base Color"].default_value[2]) print("Subsurface ", nodes["Principled BSDF"].inputs["Subsurface"].default_value)
出力結果
Base Color 0.8000000715255737
Base Color 0.0012105016503483057
Base Color 0.0
Subsurface 0.6272727251052856
Base Color 0.0012105016503483057
Base Color 0.0
Subsurface 0.6272727251052856
gluLookAtの自前実装
以下の式をそのまま実装する。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluLookAt.xml
プログラム本体
#include <gl/GLU.h> #pragma comment(lib,"glu32.lib") #pragma warning(disable:4996)
//! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; }
//! @brief IxJ行列 × JxK行列 の乗算関数 //https://suzulang.com/cpp-multmatrix44/ //! @param [out] C Cik 計算結果格納先 //! @param [in] A Aijの行列 //! @param [in] B Bjkの行列 //! @param [in] I Aの行列の行数 //! @param [in] J Aの行列の列数 //! @param [in] K Bの行列の列数 //! @return C template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrixIJK(real_tC* C, const real_tA* A, const real_tB* B, const int I, const int J, const int K) { for (int i = 0; i < I; i++) for (int k = 0; k < K; k++) { C[matijI(i, k, I)] = 0.0; for (int j = 0; j < J; j++) { C[matijI(i, k, I)] += A[matijI(i, j, I)] * B[matijI(j, k, J)]; } } return C; }
//! @brief 4x4行列の行列の積を計算する //! @param [out] C 結果の格納先 //! @param [in] A 行列A //! @param [in] B 行列B //! @return Cへのポインタ template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix44( real_tC* C, const real_tA* A, const real_tB* B){ return mult_matrixIJK(C, A, B, 4, 4, 4); }
//! @brief 移動行列を作成する //! @param [out] m 結果の格納先 //! @param [in] x ベクトルのx成分 //! @param [in] y ベクトルのy成分 //! @param [in] z ベクトルのz成分 //! @return なし template<typename real_t> void mytranslate( real_t* m, real_t x, real_t y, real_t z ) { m[0] = 1.0; m[1] = 0.0; m[2] = 0.0; m[3] = 0.0; m[4] = 0.0; m[5] = 1.0; m[6] = 0.0; m[7] = 0.0; m[8] = 0.0; m[9] = 0.0; m[10] = 1.0; m[11] = 0.0; m[12] = x; m[13] = y; m[14] = z; m[15] = 1.0; }
//! @brief 単位行列を作成する //! @param [out] m 結果の格納先 //! @return なし template<typename real_t> inline void loadidentity3(real_t* m){ m[0] = 1.0; m[1] = 0.0; m[2] = 0.0; m[3] = 0.0; m[4] = 0.0; m[5] = 1.0; m[6] = 0.0; m[7] = 0.0; m[8] = 0.0; m[9] = 0.0; m[10] = 1.0; m[11] = 0.0; m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1.0; }
//! @brief 配列にNANが入っているか確認 //! @param [in] m 評価する配列 //! @param [in] count 行列の要素数 template<typename real_t> bool chek_array_nan(const real_t* m, const size_t count) { for (size_t i = 0; i < count; i++) { if (isnan(m[i]) == true) return true; } return false; }
template<typename real_t> inline void Outer3(real_t* const dvec, real_t const* const svec1, real_t const* const svec2) { const real_t& x1 = svec1[0]; const real_t& y1 = svec1[1]; const real_t& z1 = svec1[2]; const real_t& x2 = svec2[0]; const real_t& y2 = svec2[1]; const real_t& z2 = svec2[2]; dvec[0] = static_cast<real_t>(y1 * z2 - z1 * y2); dvec[1] = static_cast<real_t>(z1 * x2 - x1 * z2); dvec[2] = static_cast<real_t>(x1 * y2 - y1 * x2); }
template<typename real_t> real_t Inner3(real_t const* const vec1, real_t const* const vec2) { const int X = 0; const int Y = 1; const int Z = 2; return ((vec1[X]) * (vec2[X]) + (vec1[Y]) * (vec2[Y]) + (vec1[Z]) * (vec2[Z])); }
template<typename real_t> real_t Length3(const real_t* const vec) { const int X = 0; const int Y = 1; const int Z = 2; return sqrt(vec[X] * vec[X] + vec[Y] * vec[Y] + vec[Z] * vec[Z]); }
template<typename real_t> bool Normalize3(real_t * const pV) { const int X = 0; const int Y = 1; const int Z = 2; real_t len; real_t& x = pV[X]; real_t& y = pV[Y]; real_t& z = pV[Z]; len = static_cast<real_t>(sqrt(x * x + y * y + z * z)); if (len < static_cast<real_t>(1e-6)) return false; len = static_cast<real_t>(1.0) / len; x *= len; y *= len; z *= len; return true; }
//! @brief gluLookAtの自前実装版 //! @param [out] M 結果の格納先 //! @param [out] eyeX カメラ位置 //! @param [out] eyeY カメラ位置 //! @param [out] eyeZ カメラ位置 //! @param [out] centerX //! @param [out] centerY //! @param [out] centerZ //! @param [out] upX //! @param [out] upY //! @param [out] upZ //! @return なし
void myglulookat( GLdouble* M, GLdouble eyeX, GLdouble eyeY, GLdouble eyeZ, GLdouble centerX, GLdouble centerY, GLdouble centerZ, GLdouble upX, GLdouble upY, GLdouble upZ) { GLdouble f[3] = { centerX - eyeX, centerY - eyeY, centerZ - eyeZ }; Normalize3(f); GLdouble UP[3] = {upX,upY,upZ}; Normalize3(UP); GLdouble s[3]; Outer3(s, f, UP); Normalize3(s); GLdouble u[3]; Outer3(u, s, f); GLdouble M0[16]; M0[ 0] = s[0]; M0[ 1] = u[0]; M0[ 2] = -f[0]; M0[ 3] = 0; M0[ 4] = s[1]; M0[ 5] = u[1]; M0[ 6] = -f[1]; M0[ 7] = 0; M0[ 8] = s[2]; M0[ 9] = u[2]; M0[10] = -f[2]; M0[11] = 0; M0[12] = 0; M0[13] = 0; M0[14] = 0; M0[15] = 1; ///////////////////////////// ///////////////////////////// GLdouble E[16]; mytranslate(E, -eyeX, -eyeY, -eyeZ); mult_matrix44(M, M0, E); if (chek_array_nan(M, 16) == true) loadidentity3(M); }
テスト用コード
void test() { glMatrixMode(GL_PROJECTION); glLoadIdentity(); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); GLdouble ex = (rand() % 1000) / 1000.0 - 0.5; GLdouble ey = (rand() % 1000) / 1000.0 - 0.5; GLdouble ez = (rand() % 1000) / 1000.0 - 0.5; GLdouble cx = (rand() % 1000) / 1000.0 - 0.5; GLdouble cy = (rand() % 1000) / 1000.0 - 0.5; GLdouble cz = (rand() % 1000) / 1000.0 - 0.5; GLdouble ux = (rand() % 1000) / 1000.0 - 0.5; GLdouble uy = (rand() % 1000) / 1000.0 - 0.5; GLdouble uz = (rand() % 1000) / 1000.0 - 0.5;
GLdouble M0[16]; gluLookAt(ex, ey, ez, cx, cy, cz, ux, uy, uz); glGetDoublev(GL_MODELVIEW_MATRIX, M0);
GLdouble M1[16]; myglulookat( M1, ex, ey, ez, cx, cy, cz, ux, uy, uz);
puts("------------------------"); for (size_t i = 0; i < 16; i++) { printf("[%d] %lf\n", i, M0[i] - M1[i]); } }
実行結果
[0] -0.000000 [1] 0.000000 [2] -0.000000 [3] 0.000000 [4] -0.000000 [5] 0.000000 [6] -0.000000 [7] 0.000000 [8] -0.000000 [9] -0.000000 [10] 0.000000 [11] 0.000000 [12] 0.000000 [13] 0.000000 [14] -0.000000 [15] 0.000000
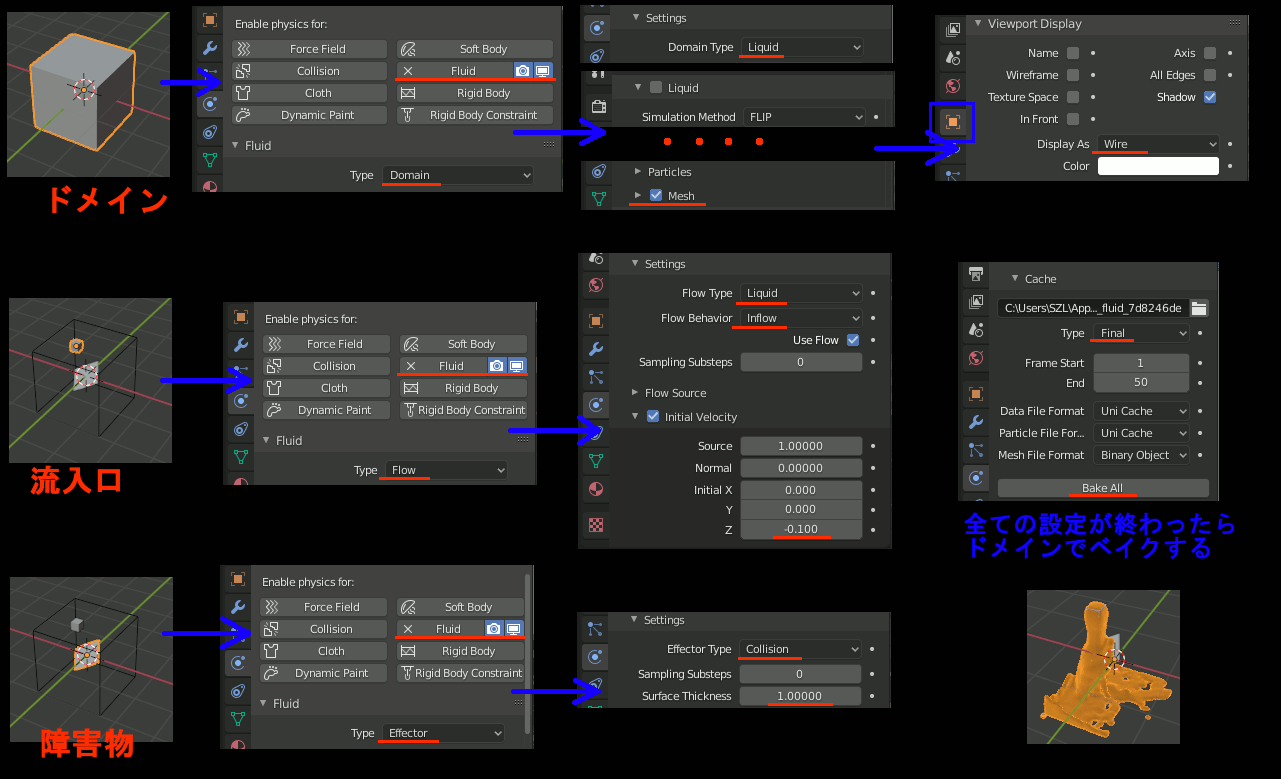
Blender 流体シミュレーションをとりあえず動かす最短の設定
Blender Sapling ,Splittingについて
Sapling Tree Gen の Branch Splitting。挙動がわかりづらかったので整理。
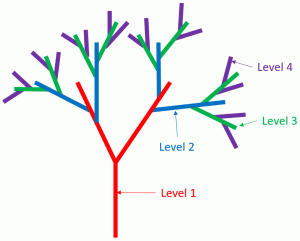
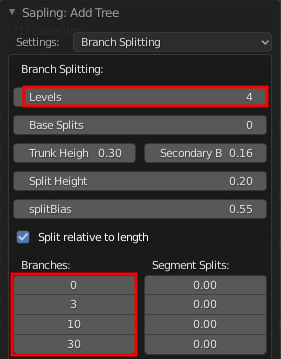
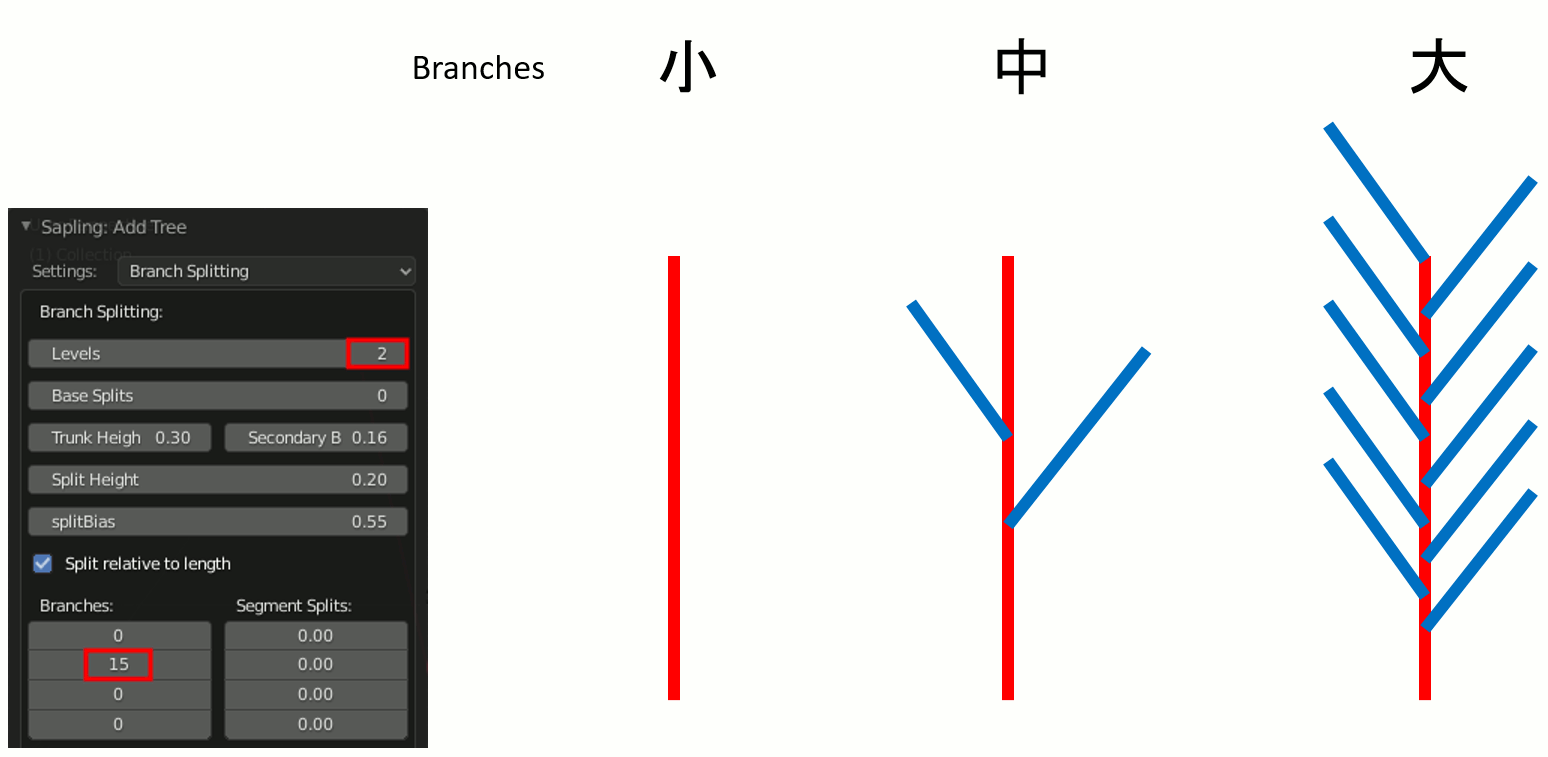
Levels,Branches
Levels ... 何レベルまで使用するかを指定
Branches ... 各レベルの枝がどれぐらい多いかを指定
例えばLevels=2の場合、図中青の枝までが出現する。
Branchesの指定で、青の枝がどれぐらい多いかを指定する
Segment Splits
そのレベルを何分割するかを指定する。
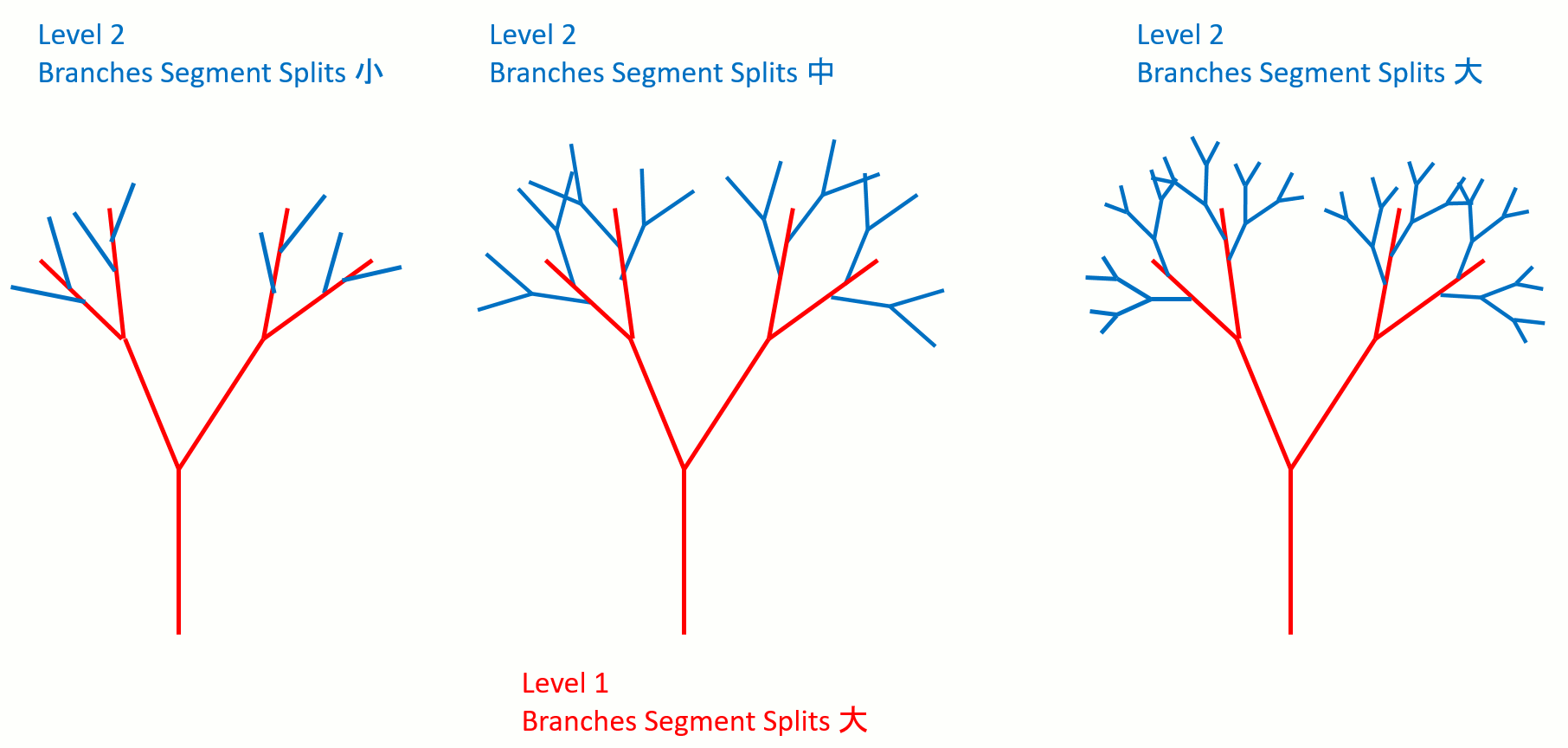
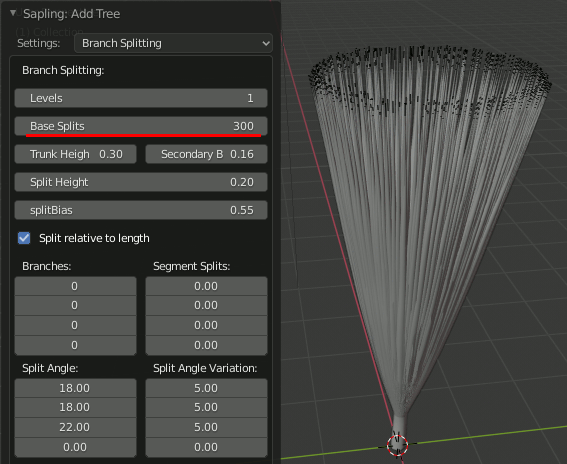
Base Split
Base splitはレベル１を何分割するかを指定する。
Leaves
葉は一番大きなレベルに出現する。
Blender CyclesでDisplacement
モディファイアを使わず、CyclesでレンダリングするときにのみDisplacementを適用する話。
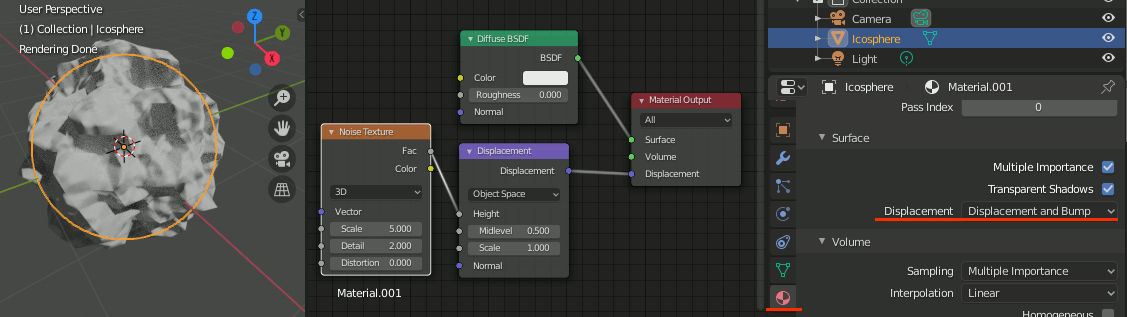
Material PropertiesのSurface内、Displacementの設定を
Displacement Only または Displacement and Bump に設定する
使用例
Blender 2.8 instancing機能について
instancing機能はオブジェクトを複製する機能と言える。検索するとParticle Hairのように見える例が散見されるが、どちらかというとArrayモディファイアに近いと思う。
というかなんでモディファイアではないんだ。
instancingの考え方
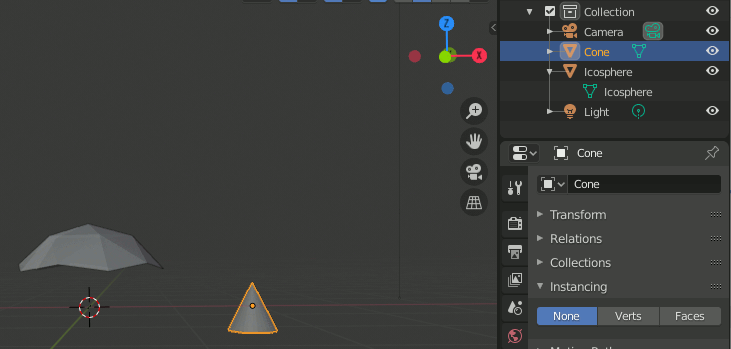
① 「複製したいオブジェクト」と「複製の基準となるオブジェクト」を用意
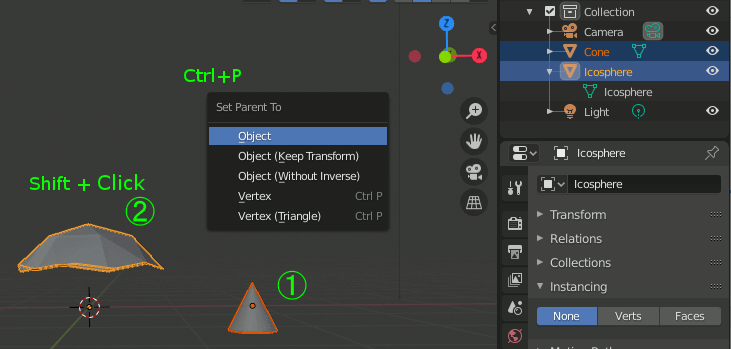
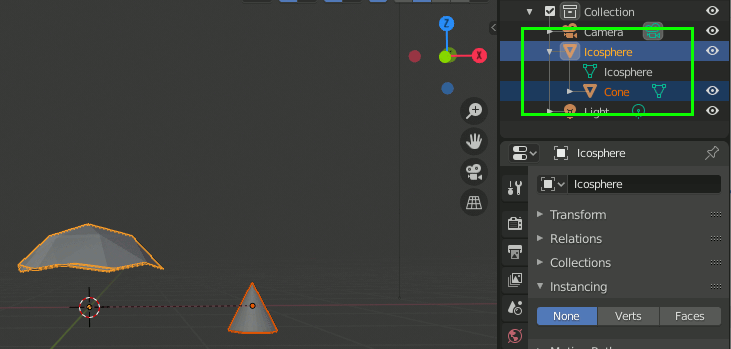
② 基準（親） － 複製したいオブジェクト（子）の関係を作る
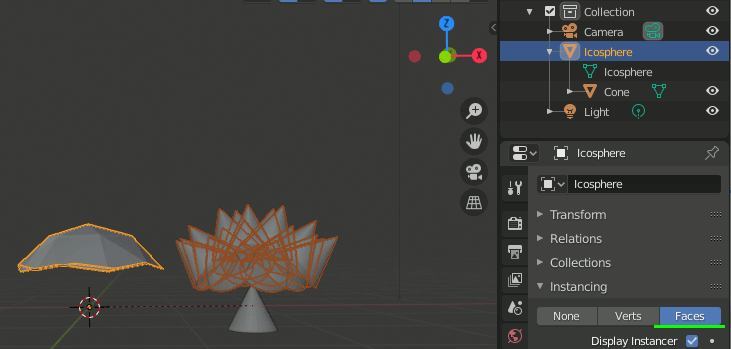
③ 複製方法（面基準か頂点基準か）を選択する
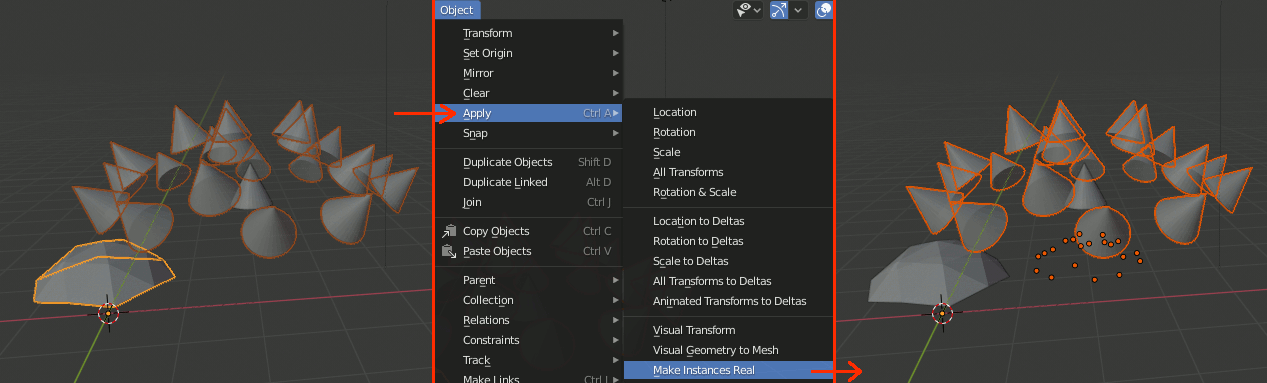
実体化
基準としたオブジェクトを選択し、[Object]→[Apply]→[Make Instances Real]で複製したオブジェクトを実体化する
二次元のN角形の頂点座標の計算
たまに欲しくなる、三角形とか五角形とかの座標計算をする。
実のところ円を描くのと全く同じ。以前円を描くプログラムを書いた。
これを書いた当時は事情によりこの方法の法が簡単だったのだけれどやはり普通の方法の方が簡単だ。
コード
//! @tparam Point2D 二次元座標を一つ表現する。operator[](int)が必要 //! @brief 多角形を作成する //! @param [out] points 作成した多角形の頂点 //! @param [in] N 頂点数 //! @param [in] radius 中心から頂点までの距離 //! @return なし template<typename Point2D> void createNgon( std::vector< Point2D >& points, const int N, const double radius = 1.0 ) { for (size_t i = 0; i < N; i++) { double t = 2 * 3.14 / N * i; double x = sin(t); double y = cos(t); Point2D p; p[0] = x * radius; p[1] = y * radius; points.push_back(p); } }
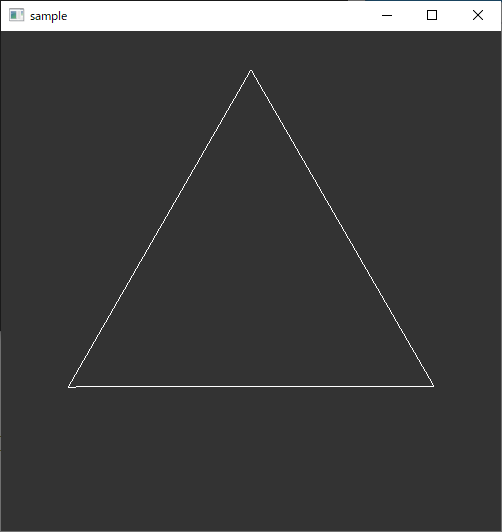
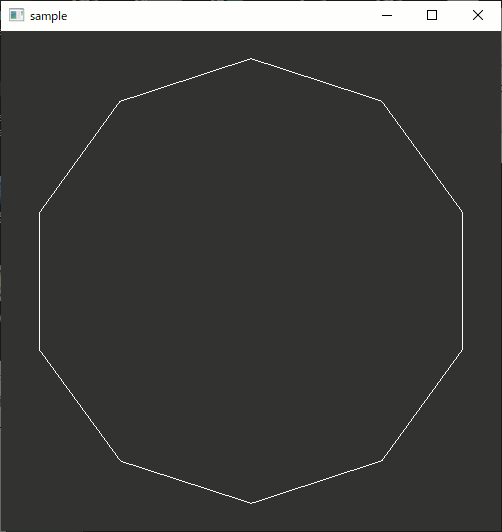
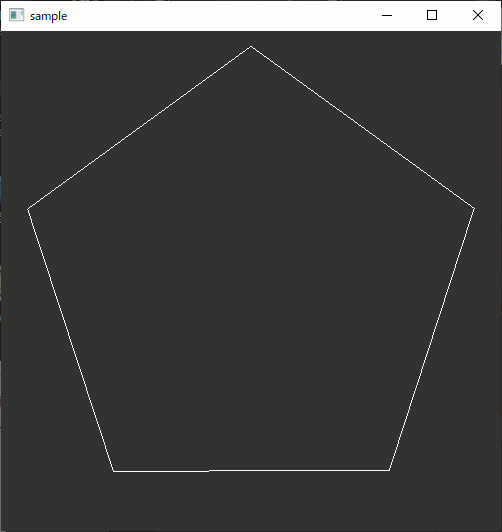
使用例
//多角形作成 std::vector<std::array<double, 2>> ngon; createNgon(ngon,3); //表示 glPointSize(1); glBegin(GL_LINE_LOOP); for (size_t i = 0; i < ngon.size(); i++) { glVertex2dv(ngon[i].data()); } glEnd();
Blender 2.8 Create Grass Fast Blender Tutorial 抜粋
これも無駄の多いチュートリアルなので抜粋する
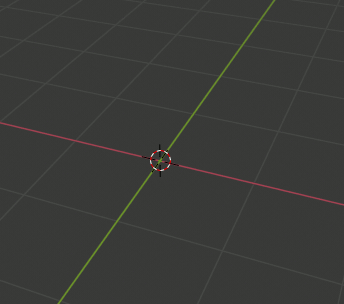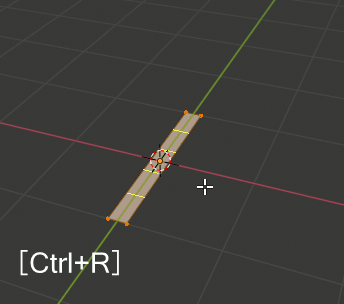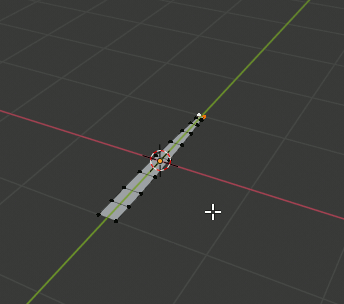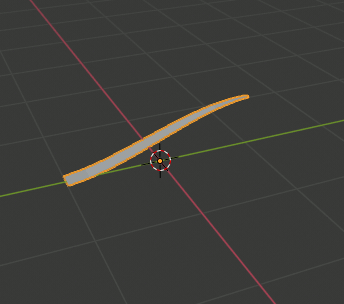
草一本を作成
[Shift+A]→[Mesh]→[Plane]でPlaneを一つ追加し、Proportional Editingを使って草一本分をモデリングする
※ なおマテリアルを設定するならこの時が一番いい。
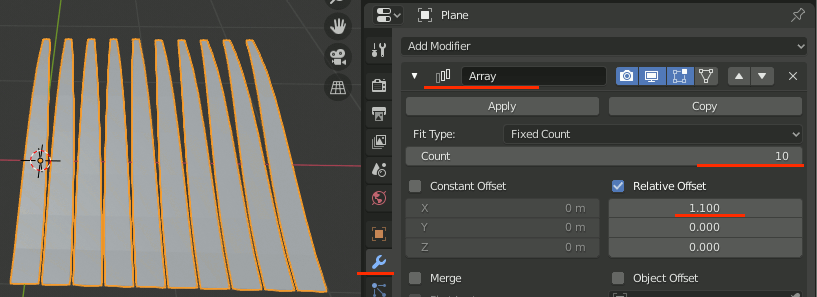
一本をコピーして100本(10x10)作成
草一本にArrayモディファイアを追加し、僅かに間隔を開けて10個複製する。
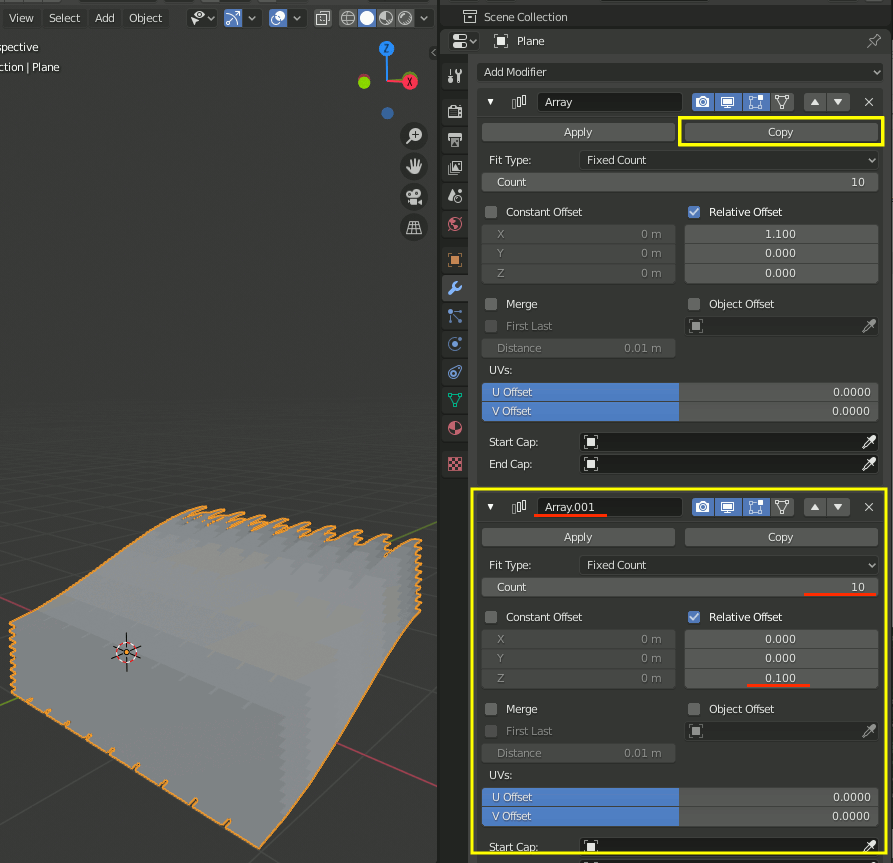
さらに、ArrayモディファイアをCopyしArray.001を作成、Relative OffsetをXを0、Zを0.1に設定する。
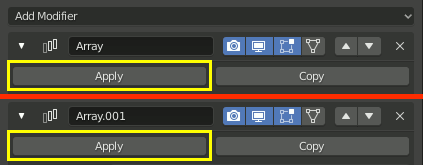
両方のArrayモディファイアをApplyする。
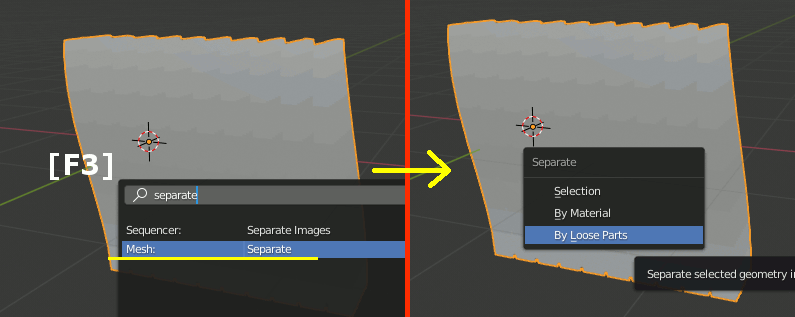
F3キーを押し、separateを検索、 By Loose Partsで非連続な部分を全て別オブジェクトに変換する
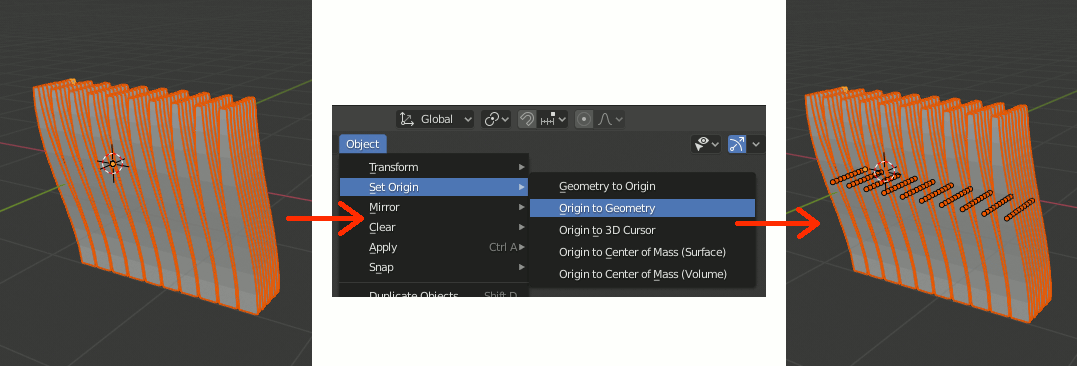
なお分割後、Origin to GeometryでOriginを各モデルの重心に移動しておく。
ランダムに再配置・結合
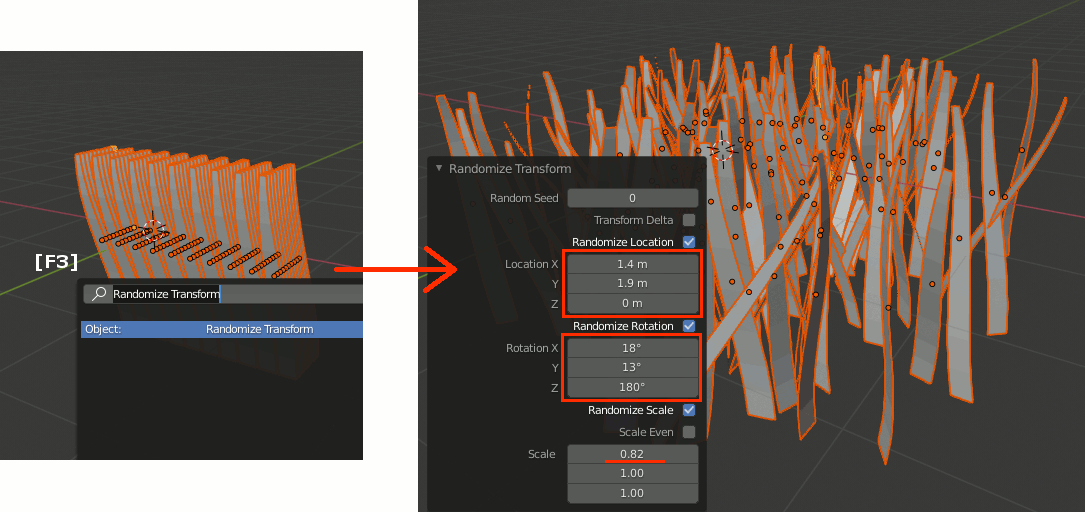
F3でRandomize Transformを検索し、Location、Rotation、Scaleを適当に設定する。この時、Rotation Zは180度回転させるが、その他は余り極端にしない。Locationを大きくしすぎると散らばりすぎる。
Randomize Transformが終わったら全部選択されている状態でCtrl+Jを押し、一つのオブジェクトにまとめる
形を整える
Proportional Editingを使って草っぽい広がり方にする
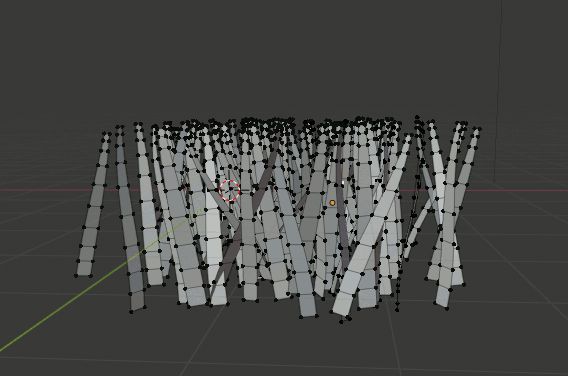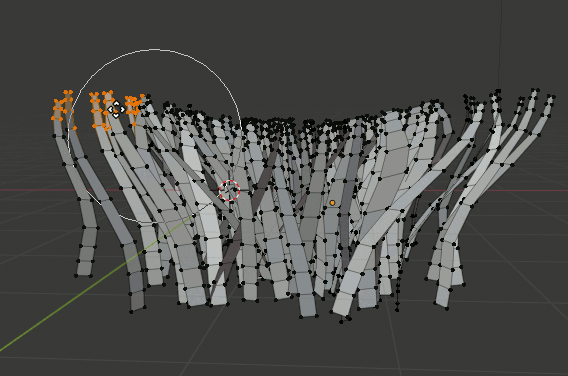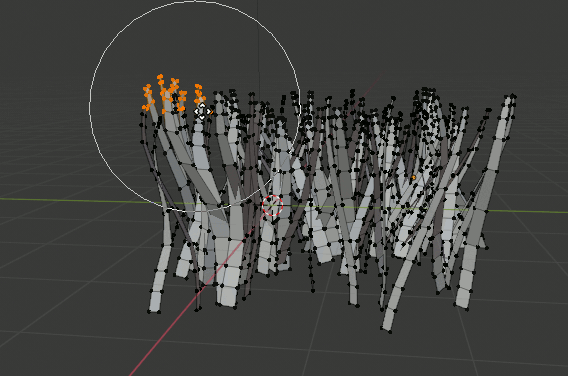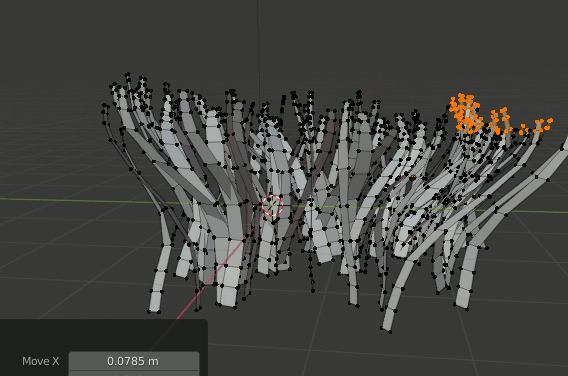
Particle hairで配置
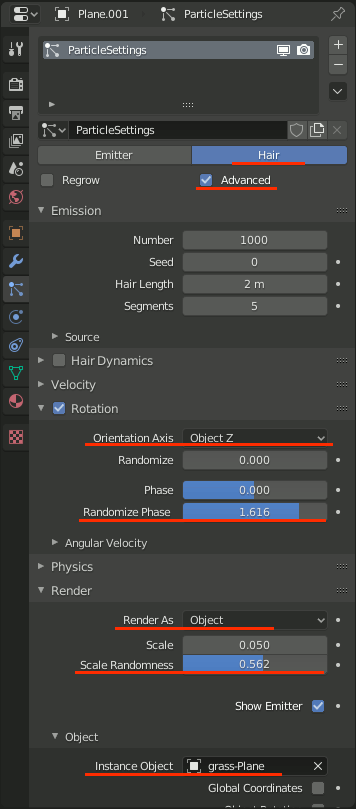
平面を追加し、Particleを追加→Hairを選択。Advancedにチェックを入れる。
Hairにオブジェクトを設定：
・Render → Render As = Object
・Render → Object → Instance Object = 草のオブジェクト
草のランダム回転：
・Rotation → Orientation Axis = ObjectZ
・Rotation → Randomize Phase = 任意
草のランダムサイズ変更：
・Render → Scale Randomness
同じ原理でテクスチャを設定した場合
https://www.cc0textures.com/view?id=Foliage001
OBBを計算する（プログラム）
プログラム本体
#pragma once #include <vector> #include <array> #include <limits> #include <valarray>
template<typename real_t> real_t Length3(const real_t * const vec) { const int X = 0; const int Y = 1; const int Z = 2; return sqrt(vec[X] * vec[X] + vec[Y] * vec[Y] + vec[Z] * vec[Z]); } template<typename real_t> bool Normalize3(real_t* const pV) { const int X = 0; const int Y = 1; const int Z = 2; real_t len; real_t& x = pV[X]; real_t& y = pV[Y]; real_t& z = pV[Z]; len = static_cast<real_t>(sqrt(x * x + y * y + z * z)); if (len < static_cast<real_t>(1e-6)) return false; len = static_cast<real_t>(1.0) / len; x *= len; y *= len; z *= len; return true; } template<typename real_t> real_t Inner3(real_t const* const vec1, real_t const* const vec2) { const int X = 0; const int Y = 1; const int Z = 2; return ((vec1[X]) * (vec2[X]) + (vec1[Y]) * (vec2[Y]) + (vec1[Z]) * (vec2[Z])); }
/*! * Jacobi法による固有値の算出 * @param[inout] a 実対称行列．計算後，対角要素に固有値が入る * @param[out] v 固有ベクトル(aと同じサイズ) * @param[in] n 行列のサイズ(n×n) * @param[in] eps 収束誤差 * @param[in] iter_max 最大反復回数 * @return 反復回数 * @see http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%B8%C7%CD%AD%C3%CD/%B8%C7%CD%AD%A5%D9%A5%AF%A5%C8%A5%EB */ template<typename real_t> int EigenJacobiMethod(real_t* a, real_t* v, int n, real_t eps = 1e-8, int iter_max = 100) { real_t bii, bij, bjj, bji; auto bim = std::vector<real_t>(n); auto bjm = std::vector<real_t>(n); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { v[i * n + j] = (i == j) ? 1.0 : 0.0; } } int cnt = 0; for (;;) { int i, j; float x = 0.0; for (int ia = 0; ia < n; ++ia) { for (int ja = 0; ja < n; ++ja) { int idx = ia * n + ja; if (ia != ja && fabs(a[idx]) > x) { i = ia; j = ja; x = std::abs(a[idx]); } } } float aii = a[i * n + i]; float ajj = a[j * n + j]; float aij = a[i * n + j]; float alpha, beta; alpha = (aii - ajj) / 2.0; beta = sqrt(alpha * alpha + aij * aij); float st, ct; ct = sqrt((1.0 + fabs(alpha) / beta) / 2.0); // sinθ st = (((aii - ajj) >= 0.0) ? 1.0 : -1.0) * aij / (2.0 * beta * ct); // cosθ // A = PAPの計算 for (int m = 0; m < n; ++m) { if (m == i || m == j) continue; float aim = a[i * n + m]; float ajm = a[j * n + m]; bim[m] = aim * ct + ajm * st; bjm[m] = -aim * st + ajm * ct; } bii = aii * ct * ct + 2.0 * aij * ct * st + ajj * st * st; bij = 0.0; bjj = aii * st * st - 2.0 * aij * ct * st + ajj * ct * ct; bji = 0.0; for (int m = 0; m < n; ++m) { a[i * n + m] = a[m * n + i] = bim[m]; a[j * n + m] = a[m * n + j] = bjm[m]; } a[i * n + i] = bii; a[i * n + j] = bij; a[j * n + j] = bjj; a[j * n + i] = bji; // V = PVの計算 for (int m = 0; m < n; ++m) { float vmi = v[m * n + i]; float vmj = v[m * n + j]; bim[m] = vmi * ct + vmj * st; bjm[m] = -vmi * st + vmj * ct; } for (int m = 0; m < n; ++m) { v[m * n + i] = bim[m]; v[m * n + j] = bjm[m]; } float e = 0.0; for (int ja = 0; ja < n; ++ja) { for (int ia = 0; ia < n; ++ia) { if (ia != ja) { e += fabs(a[ja * n + ia]); } } } if (e < eps) break; cnt++; if (cnt > iter_max) break; } return cnt; } //! @brief 固有値・固有ベクトル struct _eigen_ { double _value; //!< 固有値 double _vector[3];//!< 固有ベクトル }; //! @brief データの平均を求める //! @param [in] vec データの配列 //! @return 各要素の平均 template<typename real_t,typename PointT> void Covariance_Ave(real_t* ave,const std::vector<PointT>& vec) { // 初期化 ave[0] = 0; ave[1] = 0; ave[2] = 0; // 各要素平均 for (size_t i = 0; i < vec.size(); i++) { ave[0] += vec[i][0]; ave[1] += vec[i][1]; ave[2] += vec[i][2]; } ave[0] /= vec.size(); ave[1] /= vec.size(); ave[2] /= vec.size(); } //! @brief 共分散を求める //! @param [in] average 各要素の平均 3次元 //! @param [in] vec データ //! @param [in] param どの要素に対して求めるか。例えばxyzの時、x,yに対する共分散なら{0,1}を与える。 //! @return 偏差の積の和の要素数分の一 template<typename real_t,typename PointT> double Covariance(const real_t* const average, const std::vector<PointT>& vec, const std::array<int, 2>& param) { double sum = 0.0; for (size_t i = 0; i < vec.size(); i++) { //指定したパラメータの偏差を求める double deviation[3]; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; deviation[target] = (vec[i][target] - average[target]); } //偏差の積 double product = 1.0; for (size_t j = 0; j < param.size(); j++) { int target = param[j]; product *= deviation[target]; } //偏差の積の和を更新 sum += product; } //偏差の積の和のN分の一 return 1.0 / vec.size() * sum; } //! @brief データを主成分分析する //! @param [out] average 全データの各要素の平均 //! @param [out] ev 固有値と固有ベクトル //! @param [in] pt 三次元の座標値一覧 //! @return なし template<typename PointT> void PrincipalComponentAnalysis3D(_eigen_* e, const std::vector<PointT>& pt) { double average[3]; //各要素の平均を求める。 //これは共分散を求めるときに (x[i] - xの平均)×(y[i] - yの平均) 等の計算が必要なため Covariance_Ave(average, pt); //共分散を求める //第三引数の{0,0}はxxを表す。xyなら{0,1}。これはデータがxyzの順に並んでいる事が前提。 double Sxx = static_cast<double>(Covariance(average, pt, { 0, 0 })); double Sxy = static_cast<double>(Covariance(average, pt, { 0, 1 })); double Sxz = static_cast<double>(Covariance(average, pt, { 0, 2 })); double Syy = static_cast<double>(Covariance(average, pt, { 1, 1 })); double Syz = static_cast<double>(Covariance(average, pt, { 1, 2 })); double Szz = static_cast<double>(Covariance(average, pt, { 2, 2 })); // 分散共分散行列 double a[3 * 3] = { Sxx,Sxy,Sxz, Sxy,Syy,Syz, Sxz,Syz,Szz }; double eigen[3 * 3]; EigenJacobiMethod(a, eigen, 3); // eigenの対角線が固有値となっている e[0]._value = eigen[0]; e[0]._vector[0] = eigen[0]; e[0]._vector[1] = eigen[3]; e[0]._vector[2] = eigen[6]; e[1]._value = eigen[4]; e[1]._vector[0] = eigen[1]; e[1]._vector[1] = eigen[4]; e[1]._vector[2] = eigen[7]; e[2]._value = eigen[8]; e[2]._vector[0] = eigen[2]; e[2]._vector[1] = eigen[5]; e[2]._vector[2] = eigen[8]; }
// OBBを表現する構造体
struct OBBObject { double corner[3]; //OBBの角 double vectorU[3]; //各辺の方向と長さ double vectorV[3]; double vectorN[3]; };
inline std::valarray<double> shift_centersUV( const std::valarray<double>& centerU, const std::valarray<double>& centerV, const std::valarray<double>& centerN, const std::valarray<double>& vectorU, const std::valarray<double>& vectorV, const std::valarray<double>& vectorN ) { ////////////////////////////////////////// // vector vectorU→centerV std::valarray<double> vRG = centerV - centerU; double Rlen = Inner3(&vectorU[0], &vRG[0]); Rlen /= Length3(&vectorU[0]); std::valarray<double> direction_uv = vectorU; Normalize3(&direction_uv[0]); direction_uv *= -Rlen; glLineWidth(2); glColor3d(1, 0, 0); ////////////////////////////////////////// // vector centerV→centerU std::valarray<double> vGR = centerU - centerV; double Glen = Inner3(¢erV[0], &vGR[0]); Glen /= Length3(¢erV[0]); std::valarray<double> direction_vc = centerV; Normalize3(&direction_vc[0]); direction_vc *= -Glen; ////////////////////////////////////////// return direction_uv + direction_vc; } inline std::valarray<double> get_a_corner( const std::valarray<double>& centerU, const std::valarray<double>& centerV, const std::valarray<double>& centerN, const std::valarray<double>& vectorU, const std::valarray<double>& vectorV, const std::valarray<double>& vectorN ) { std::valarray<double> ret; ///////////////////////////// // OBBの中央を見つける ///////////////////////////// std::valarray<double> trueCenter = centerN + shift_centersUV( centerU, centerV, centerN, vectorU, vectorV, vectorN ); /////////////////////////////////////// // OBBの中央から各辺の半分ずつ移動する /////////////////////////////////////// ret = trueCenter - (vectorU/2.0) - (vectorV/2.0) - (vectorN/2.0); return ret; } //! @brief 点群を囲むOBBを求める //! @param [in] obb BoundingBoxを表現する構造体 //! @param [in] pt 計算対象の頂点 template<typename PointT> void CalcOBB(OBBObject* obb, const std::vector<PointT> pt) { using scalar_t = double; _eigen_ e[3]; PrincipalComponentAnalysis3D(e, pt); //降順ソート std::sort(std::begin(e), std::end(e), [](const _eigen_ & e1, const _eigen_ & e2) { return e1._value > e2._value; }); scalar_t obbLen[3];//ボックス辺長さ std::array<std::valarray<double>, 3> centerd; centerd[0] = std::valarray<double>(3); centerd[1] = std::valarray<double>(3); centerd[2] = std::valarray<double>(3); for (int k = 0; k < 3; k++) { scalar_t inner_k_min = (std::numeric_limits<scalar_t>::max)(); scalar_t inner_k_max = std::numeric_limits<scalar_t>::lowest(); //第 k+1 主成分とすべての頂点の内積のうち最大・最小を取り出す for (size_t i = 0; i < pt.size(); i++) { scalar_t p[3] = { pt[i][0], pt[i][1], pt[i][2] }; inner_k_min = (std::min)( Inner3(p, e[k]._vector), inner_k_min ); inner_k_max = (std::max)( Inner3(p, e[k]._vector), inner_k_max ); } obbLen[k] = (inner_k_max - inner_k_min); scalar_t tmp = (inner_k_max + inner_k_min) / 2.0; centerd[k][0] = e[k]._vector[0] * tmp; centerd[k][1] = e[k]._vector[1] * tmp; centerd[k][2] = e[k]._vector[2] * tmp; } /////////////////////////////// std::valarray<double> vecu = { e[0]._vector[0] * obbLen[0], e[0]._vector[1] * obbLen[0], e[0]._vector[2] * obbLen[0] }; std::valarray<double> vecv = { e[1]._vector[0] * obbLen[1], e[1]._vector[1] * obbLen[1], e[1]._vector[2] * obbLen[1] }; std::valarray<double> vecn = { e[2]._vector[0] * obbLen[2], e[2]._vector[1] * obbLen[2], e[2]._vector[2] * obbLen[2] }; std::valarray<double> ret = get_a_corner( centerd[0], centerd[1], centerd[2], vecu, vecv, vecn ); obb->corner[0] = ret[0]; obb->corner[1] = ret[1]; obb->corner[2] = ret[2]; obb->vectorU[0] = vecu[0]; obb->vectorU[1] = vecu[1]; obb->vectorU[2] = vecu[2]; obb->vectorV[0] = vecv[0]; obb->vectorV[1] = vecv[1]; obb->vectorV[2] = vecv[2]; obb->vectorN[0] = vecn[0]; obb->vectorN[1] = vecn[1]; obb->vectorN[2] = vecn[2]; }
呼び出し方
std::vector<std::vector<double> > points; //点群の読み込み先 read_xyz(points,"C:\\test\\Suzanne.xyz",' '); //点群読み込み CalcOBB(&obb, points);// OBB計算
なお以下はxyzファイル読み込み
//! @brief separator区切りの実数の一覧を読み込む //! @details xyzフォーマットは正式な規格として存在しないらしいので、ある程度の柔軟性を持たせる //! @param [out] ret 結果を格納する配列の配列 //! @param [in] filename ファイル名 //! @param [in] separator 区切り文字 //! @return なし template<typename scalar_t> void read_xyz(std::vector<std::vector<scalar_t> >& ret,const char* filename, const char separator) { std::ifstream ifs(filename); std::string str; while (std::getline(ifs, str)) { std::stringstream line{ str }; std::string value; std::vector<scalar_t> tmp; while (getline(line, value, separator)){ tmp.push_back(std::atof(value.c_str())); } ret.push_back(tmp); } }
OBB 表示関数
//! @brief 立方体を描画 //! @param [in] width 立方体の一辺の長さ //! @return なし void draw_obb(const OBBObject& obb) { double xs = obb.corner[0]; double ys = obb.corner[1]; double zs = obb.corner[2]; glEnable(GL_DEPTH_TEST); glFrontFace(GL_CCW);//時計回りが表 glEnable(GL_CULL_FACE);//カリングを有効にする glBegin(GL_LINE_LOOP); glColor3d(0.5, 0.5, 1.0); glVertex3d(xs, ys, zs);// glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2]); glVertex3d( xs + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2]); glEnd(); glBegin(GL_LINE_LOOP); glColor3d(0.0, 0.0, 1.0); glVertex3d( xs + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorU[2] + obb.vectorV[2]); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorN[2] + obb.vectorU[2]); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2]);// glEnd(); glBegin(GL_LINE_LOOP); glColor3d(1.0, 0.0, 0.0); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2] ); glVertex3d( xs + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorN[2] + obb.vectorV[2] ); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2] ); glVertex3d(xs, ys, zs);// glEnd(); glBegin(GL_LINE_LOOP); glColor3d(1.0, 0.5, 0.5); glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2]);// glVertex3d( xs + obb.vectorU[0] + obb.vectorN[0], ys + obb.vectorU[1] + obb.vectorN[1], zs + obb.vectorU[2] + obb.vectorN[2] ); glVertex3d( xs + obb.vectorU[0] + obb.vectorN[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorN[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorN[2] + obb.vectorV[2] ); glVertex3d( xs + obb.vectorU[0] + obb.vectorV[0], ys + obb.vectorU[1] + obb.vectorV[1], zs + obb.vectorU[2] + obb.vectorV[2] ); glEnd(); glLineWidth(2); glColor3d(0, 1, 0); glBegin(GL_LINE_LOOP); glVertex3d( xs, ys, zs); glVertex3d( xs + obb.vectorN[0], ys + obb.vectorN[1], zs + obb.vectorN[2] ); glVertex3d( xs + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorN[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorU[0], ys + obb.vectorU[1], zs + obb.vectorU[2] ); glEnd(); glColor3d(0.5, 1, 0.5); glBegin(GL_LINE_LOOP); glVertex3d( xs + obb.vectorV[0] + obb.vectorU[0], ys + obb.vectorV[1] + obb.vectorU[1], zs + obb.vectorV[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorV[0] + obb.vectorN[0] + obb.vectorU[0], ys + obb.vectorV[1] + obb.vectorN[1] + obb.vectorU[1], zs + obb.vectorV[2] + obb.vectorN[2] + obb.vectorU[2] ); glVertex3d( xs + obb.vectorV[0] + obb.vectorN[0], ys + obb.vectorV[1] + obb.vectorN[1], zs + obb.vectorV[2] + obb.vectorN[2] ); glVertex3d( xs + obb.vectorV[0], ys + obb.vectorV[1], zs + obb.vectorV[2]); glEnd(); glDisable(GL_CULL_FACE);//カリングを無効にする }
