月火水木金土日
gluUnProjectを自前実装する
逆行列や行列の積に関しては以前の記事参照:
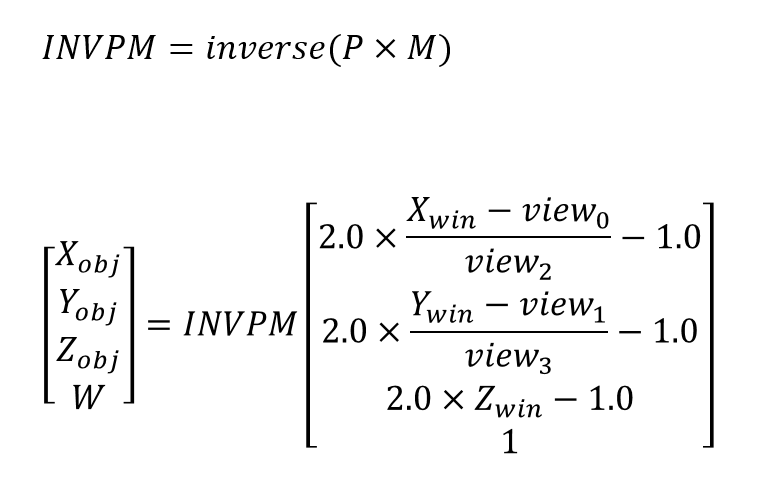
gluUnProjectもkhronosが言っている通りの式では結果が違ってしまうので実装例を確認してそちらに合わせた。
https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml
template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix44(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 4); } template< typename real_tC, typename real_tA, typename real_tB> real_tC* mult_matrix_vec41(real_tC* C, const real_tA* A, const real_tB* B) { return mult_matrixIJK(C, A, B, 4, 4, 1); }
/////////////////////////////////////// // gluUnProject // https://www.khronos.org/registry/OpenGL-Refpages/gl2.1/xhtml/gluUnProject.xml //! @brief gluUnProjectの自前実装版 //! @param [in] winX 画面上のX座標 //! @param [in] winY 画面上のY座標 //! @param [in] winZ 画面上のZ座標 //! @param [in] model モデルビュー行列 //! @param [in] proj プロジェクション行列 //! @param [in] ビューポート x,y,width,height //! @param [out] objX 空間座標のX //! @param [out] objY 空間座標のY //! @param [out] objZ 空間座標のZ //! @retval true 計算成功 //! @retval false 計算失敗
template<typename real_t> bool myUnProject( real_t winX, real_t winY, real_t winZ, const real_t* model, const real_t* proj, const int* view, real_t* objX, real_t* objY, real_t* objZ ) { real_t pm[16]; real_t invpm[16]; mult_matrix44(pm, proj, model);//pm = P×M bool ret = inverse_matrix44(invpm, pm);// pmの逆行列 if (ret == false) return false; real_t v[4] = { 2 * (winX - view[0]) / view[2] - 1.0 , 2 * (winY - view[1]) / view[3] - 1.0 , 2 * winZ - 1.0, 1 }; real_t vd[4]; mult_matrix_vec41(vd, invpm, v); // vd = invpm × v *objX = vd[0] / vd[3]; *objY = vd[1] / vd[3]; *objZ = vd[2] / vd[3]; return true; }
動作検証
int WIDTH = 300; int HEIGHT = 400; void disp(void) { glViewport(0, 0, WIDTH, HEIGHT); glMatrixMode(GL_PROJECTION); glPushMatrix(); glLoadIdentity(); gluPerspective(45, 0.5, 0.1, 2.5); glMatrixMode(GL_MODELVIEW); glPushMatrix(); glLoadIdentity(); glTranslated(-1, 0, -2); glRotated(1.5, 1.0, 1.0, 1.0);
////作成した変換行列を取得する GLdouble modeld[16]; glGetDoublev(GL_MODELVIEW_MATRIX, modeld); GLdouble projd[16]; glGetDoublev(GL_PROJECTION_MATRIX, projd); GLint view[4]; glGetIntegerv(GL_VIEWPORT, view);
// 三次元座標(出力) double objx, objy, objz; // 二次元ピクセル座標(入力) double winx = (rand() % 1000) / 100.0, winy = (rand() % 1000) / 100.0, winz = (rand() % 1000) / 100.0;
gluUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz); printf("glu %lf %lf %lf\n", objx, objy, objz);
myUnProject( winx, winy, winz, modeld, projd, view, &objx, &objy, &objz ); printf("my %lf %lf %lf\n", objx, objy, objz);
puts("-----------"); glMatrixMode(GL_PROJECTION); glPopMatrix(); glMatrixMode(GL_MODELVIEW); glPopMatrix(); }
glu -1.165678 0.640021 1.701902 my -1.165678 0.640021 1.701902 ----------- glu -0.973079 0.946809 1.542299 my -0.973079 0.946809 1.542299 ----------- glu -0.734826 1.333922 1.296449 my -0.734826 1.333922 1.296449 ----------- glu -1.907228 1.907111 0.176182 my -1.907228 1.907111 0.176182 ----------- glu -1.917435 0.198937 1.894649 my -1.917435 0.198937 1.894649 ----------- glu -1.973992 0.975493 1.354121 my -1.973992 0.975493 1.354121 ----------- glu -1.364160 1.002119 1.417683 my -1.364160 1.002119 1.417683 ----------- glu -0.614162 0.527975 1.841761 my -0.614162 0.527975 1.841761 ----------- glu -0.323812 0.312351 1.947271 my -0.323812 0.312351 1.947271 -----------