月火水木金土日
OpenGLの行列の表記とC/C++での扱い
やっていると時々混乱し、致命的なミスを犯すので確認しておきたい。
まず、以下はOpenGLの移動行列。一番右側の列に移動パラメータが入る。
そしてこれは揺るがない。数学の世界、概念の世界の話なので。
次に、C/C++でこれがどう表現されているのか。以下のプログラムで確認する。
//OpenGLの機能で変換行列を作成する
glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2);
//作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf);
//取得した変換行列を表示する for (int i = 0; i < 16; i++) { printf("[%2d] = %3.0lf\n",i, modelf[i]); }
結果
[ 0] = 1
[ 1] = 0
[ 2] = 0
[ 3] = 0
[ 4] = 0
[ 5] = 1
[ 6] = 0
[ 7] = 0
[ 8] = 0
[ 9] = 0
[10] = 1
[11] = 0
[12] = -1
[13] = 0
[14] = -2
[15] = 1
[ 1] = 0
[ 2] = 0
[ 3] = 0
[ 4] = 0
[ 5] = 1
[ 6] = 0
[ 7] = 0
[ 8] = 0
[ 9] = 0
[10] = 1
[11] = 0
[12] = -1
[13] = 0
[14] = -2
[15] = 1
これをそのまま4要素区切りで表示すると、以下のように転置でもしたかのように見えてしまう。これはバグでも何でも無く、「現実世界の実物がプログラム中でどう表現されているか」という問題でしかない。
//OpenGLの機能で変換行列を作成する glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2); //作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf); //取得した変換行列を表示する for (int i = 0; i < 16; i++) { if (i % 4 == 0) puts(""); printf("%3.0lf", modelf[i]); }
結果
1 0 0 0 0 1 0 0 0 0 1 0 -1 0 -2 1
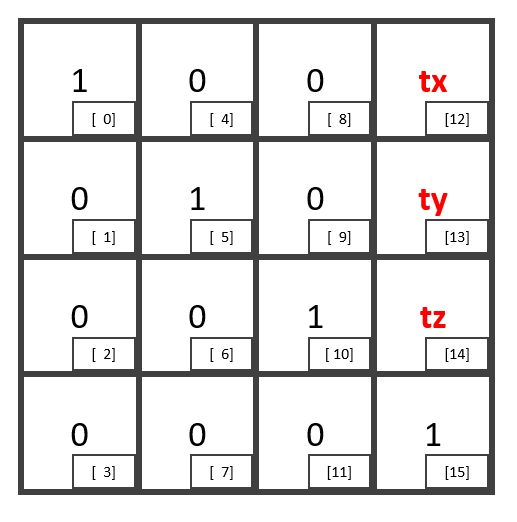
そして、OpenGLでは”行列”を、配列を用いて以下の形で表現している。
この配列に対して、数学的にアクセスしたい場合、以下のような計算で要素番号を求める。
//! @brief 4x4行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 inline int matij4(const int i, const int j) { return i + 4 * j; }
より一般的なアクセス
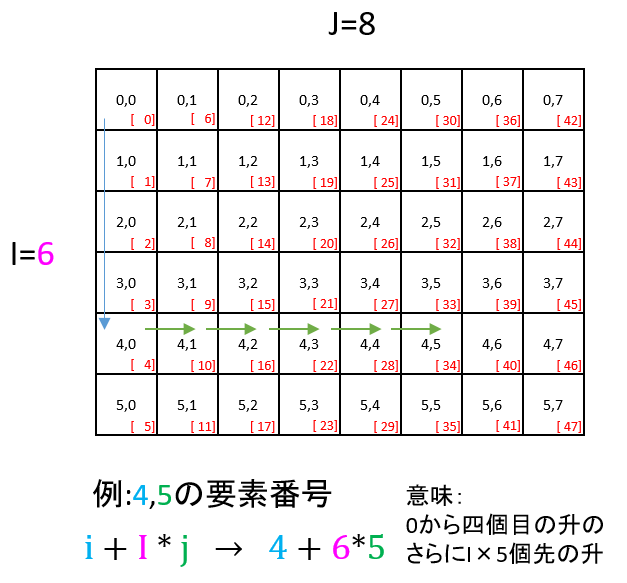
OpenGLの行列は4x4や3x3だけ考えればいいが、より一般的な行列演算関数の中でi,jから行列の添え字に変換するにはどうすればいいか。以下のような計算を行う。
//! @brief IxJ行列の i,j の要素にアクセスする //! @param [in] i 行番号 //! @param [in] j 列番号 //! @param [in] I 行数 inline int matijI(const int i, const int j, const int I) { return i + I * j; }
この考え方ではまず行を調整し、現在位置から一列の要素数×列番号だけ移動する。(※一列の要素数==行数、一行の要素数==列数)
OpenGL形式の表現の行列を表示する関数
関数本体
//! @brief 指定した行列を表示する関数
//! @param [in] m 行列を表す一次元配列
//! @param [in] format printf形式の書式
//! @param [in] I 行数
//! @param [in] J 列数
template<typename real_t> inline std::string mat_to_string(const real_t* m, const char* format,int I,int J) { std::stringstream s; char tmp[100]; for (int i = 0; i < I; i++) { for (int j = 0; j < J; j++) { sprintf(tmp, format, m[matijI(i, j,I)] ); s << tmp << " "; } s << "\n"; } return s.str(); }
使用例
//OpenGLの機能で変換行列を作成する glMatrixMode(GL_MODELVIEW); glTranslated(-1, 0, -2); //作成した変換行列を取得する GLfloat modelf[16]; glGetFloatv(GL_MODELVIEW_MATRIX, modelf); std::cout << mat_to_string(modelf, "%02.3f", 4, 4);
結果
数学的に表示できていることを確認する。
1.000 0.000 0.000 -1.000 0.000 1.000 0.000 0.000 0.000 0.000 1.000 -2.000 0.000 0.000 0.000 1.000