月火水木金土日
4×4の逆行列を求める関数
3DCGには欠かせない4×4行列の逆行列を求める関数を自前実装する。
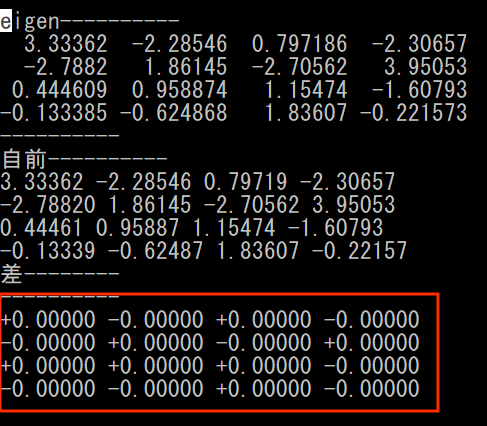
動作チェックはEigenとの差を見て判断する。
逆行列を求める関数
namespace matcalc {
//誤差の定義 template<typename T> struct real_error {static constexpr float value = (float)1e-7;}; template<> struct real_error<double> { static constexpr double value = 1e-15; }; //! @brief 誤差の閾値未満かをチェック //! @param [in] value 検査する値 //! @retval true 値の絶対値は閾値より小さい //! @retval false 値の絶対値は閾値より大きい template<typename T> inline bool is_error(const T value) { return abs(value) < real_error<T>::value; }
//! @brief 4x4行列の行列式を取得 //! @param [in] dm16 4x4行列 //! @return 行列式 template<typename real_t> inline auto determinant44(const real_t* dm16) { using scalar_t = decltype(dm16[0]); const scalar_t a11 = dm16[0]; const scalar_t a12 = dm16[1]; const scalar_t a13 = dm16[2]; const scalar_t a14 = dm16[3]; const scalar_t a21 = dm16[4]; const scalar_t a22 = dm16[5]; const scalar_t a23 = dm16[6]; const scalar_t a24 = dm16[7]; const scalar_t a31 = dm16[8]; const scalar_t a32 = dm16[9]; const scalar_t a33 = dm16[10]; const scalar_t a34 = dm16[11]; const scalar_t a41 = dm16[12]; const scalar_t a42 = dm16[13]; const scalar_t a43 = dm16[14]; const scalar_t a44 = dm16[15]; return a11 * a22* a33* a44 + a11 * a23 * a34 * a42 + a11 * a24 * a32 * a43 + a12 * a21 * a34 * a43 + a12 * a23 * a31 * a44 + a12 * a24 * a33 * a41 + a13 * a21 * a32 * a44 + a13 * a22 * a34 * a41 + a13 * a24 * a31 * a42 + a14 * a21 * a33 * a42 + a14 * a22 * a31 * a43 + a14 * a23 * a32 * a41 - a11 * a22 * a34 * a43 - a11 * a23 * a32 * a44 - a11 * a24 * a33 * a42 - a12 * a21 * a33 * a44 - a12 * a23 * a34 * a41 - a12 * a24 * a31 * a43 - a13 * a21 * a34 * a42 - a13 * a22 * a31 * a44 - a13 * a24 * a32 * a41 - a14 * a21 * a32 * a43 - a14 * a22 * a33 * a41 - a14 * a23 * a31 * a42; }
//! @brief 4x4行列の逆行列を取得 //! @param [out] dst_dm16 結果を格納する一次元配列 //! @param [in] src_dm16 元の行列 //! @retval true 成功した //! @retval false 行列式の大きさが小さすぎて失敗した template<typename real_t> inline bool inverse_matrix44(real_t* dst_dm16, const real_t* src_dm16) { using s_scalar_t = decltype(src_dm16[0]); using d_scalar_t = decltype(dst_dm16[0]); real_t a11 = src_dm16[0]; real_t a12 = src_dm16[1]; real_t a13 = src_dm16[2]; real_t a14 = src_dm16[3]; real_t a21 = src_dm16[4]; real_t a22 = src_dm16[5]; real_t a23 = src_dm16[6]; real_t a24 = src_dm16[7]; real_t a31 = src_dm16[8]; real_t a32 = src_dm16[9]; real_t a33 = src_dm16[10]; real_t a34 = src_dm16[11]; real_t a41 = src_dm16[12]; real_t a42 = src_dm16[13]; real_t a43 = src_dm16[14]; real_t a44 = src_dm16[15]; real_t& b11 = dst_dm16[0]; real_t& b12 = dst_dm16[1]; real_t& b13 = dst_dm16[2]; real_t& b14 = dst_dm16[3]; real_t& b21 = dst_dm16[4]; real_t& b22 = dst_dm16[5]; real_t& b23 = dst_dm16[6]; real_t& b24 = dst_dm16[7]; real_t& b31 = dst_dm16[8]; real_t& b32 = dst_dm16[9]; real_t& b33 = dst_dm16[10]; real_t& b34 = dst_dm16[11]; real_t& b41 = dst_dm16[12]; real_t& b42 = dst_dm16[13]; real_t& b43 = dst_dm16[14]; real_t& b44 = dst_dm16[15]; b11 = a22 * a33 * a44 + a23 * a34 * a42 + a24 * a32 * a43 - a22 * a34 * a43 - a23 * a32 * a44 - a24 * a33 * a42; b12 = a12 * a34 * a43 + a13 * a32 * a44 + a14 * a33 * a42 - a12 * a33 * a44 - a13 * a34 * a42 - a14 * a32 * a43; b13 = a12 * a23 * a44 + a13 * a24 * a42 + a14 * a22 * a43 - a12 * a24 * a43 - a13 * a22 * a44 - a14 * a23 * a42; b14 = a12 * a24 * a33 + a13 * a22 * a34 + a14 * a23 * a32 - a12 * a23 * a34 - a13 * a24 * a32 - a14 * a22 * a33; b21 = a21 * a34 * a43 + a23 * a31 * a44 + a24 * a33 * a41 - a21 * a33 * a44 - a23 * a34 * a41 - a24 * a31 * a43; b22 = a11 * a33 * a44 + a13 * a34 * a41 + a14 * a31 * a43 - a11 * a34 * a43 - a13 * a31 * a44 - a14 * a33 * a41; b23 = a11 * a24 * a43 + a13 * a21 * a44 + a14 * a23 * a41 - a11 * a23 * a44 - a13 * a24 * a41 - a14 * a21 * a43; b24 = a11 * a23 * a34 + a13 * a24 * a31 + a14 * a21 * a33 - a11 * a24 * a33 - a13 * a21 * a34 - a14 * a23 * a31; b31 = a21 * a32 * a44 + a22 * a34 * a41 + a24 * a31 * a42 - a21 * a34 * a42 - a22 * a31 * a44 - a24 * a32 * a41; b32 = a11 * a34 * a42 + a12 * a31 * a44 + a14 * a32 * a41 - a11 * a32 * a44 - a12 * a34 * a41 - a14 * a31 * a42; b33 = a11 * a22 * a44 + a12 * a24 * a41 + a14 * a21 * a42 - a11 * a24 * a42 - a12 * a21 * a44 - a14 * a22 * a41; b34 = a11 * a24 * a32 + a12 * a21 * a34 + a14 * a22 * a31 - a11 * a22 * a34 - a12 * a24 * a31 - a14 * a21 * a32; b41 = a21 * a33 * a42 + a22 * a31 * a43 + a23 * a32 * a41 - a21 * a32 * a43 - a22 * a33 * a41 - a23 * a31 * a42; b42 = a11 * a32 * a43 + a12 * a33 * a41 + a13 * a31 * a42 - a11 * a33 * a42 - a12 * a31 * a43 - a13 * a32 * a41; b43 = a11 * a23 * a42 + a12 * a21 * a43 + a13 * a22 * a41 - a11 * a22 * a43 - a12 * a23 * a41 - a13 * a21 * a42; b44 = a11 * a22 * a33 + a12 * a23 * a31 + a13 * a21 * a32 - a11 * a23 * a32 - a12 * a21 * a33 - a13 * a22 * a31; auto detA = determinant44(src_dm16); if (is_error(detA) == true) return false; detA = static_cast<decltype(detA)>(1.0) / detA; for (int i = 0; i < 16; i++) { dst_dm16[i] *= detA; } return true; }
}
動作チェック
#include<Eigen/Dense> #include "inversematrix.hpp" //自前実装版 void inversematrix_check() { ///////////////////////////////////////////// // 元データ double base[16]; for (size_t i = 0; i < 16; i++) { base[i] = rand() % 1000 / 1000.0; }
///////////////////////////////////////////// // Eigenで求める Eigen::MatrixXd eg(4, 4); eg << base[0], base[1], base[2], base[3], base[4], base[5], base[6], base[7], base[8], base[9], base[10], base[11], base[12], base[13], base[14], base[15]; auto inv = eg.inverse(); std::cout << "eigen----------" << std::endl; std::cout << inv << std::endl; std::cout << "----------" << std::endl;
///////////////////////////////////////////// //自前実装版 double* A = new double[4 * 4]{ base[0], base[1], base[2], base[3] , base[4], base[5], base[6], base[7] , base[8], base[9], base[10], base[11] , base[12], base[13], base[14], base[15] }; double* B = new double[4 * 4]; matcalc::inverse_matrix44(B, A); #pragma warning(push) #pragma warning(disable:4996) std::cout << "自前----------" << std::endl; for (int i = 0; i < 4; i++) { for (int j = 0; j < 4; j++) { printf("%0.5lf", B[i*4+ j]); printf(" "); } puts(""); }
std::cout << "差--------" << std::endl; std::cout << "----------" << std::endl; for (int i = 0; i < 4; i++) { for (int j = 0; j < 4; j++) { printf("%+0.5lf", B[i * 4 + j]-inv(i,j)); printf(" "); } puts(""); }
std::cout << std::endl << std::endl << std::endl; #pragma warning(pop) }