ICO球の作り方（１）

考え方

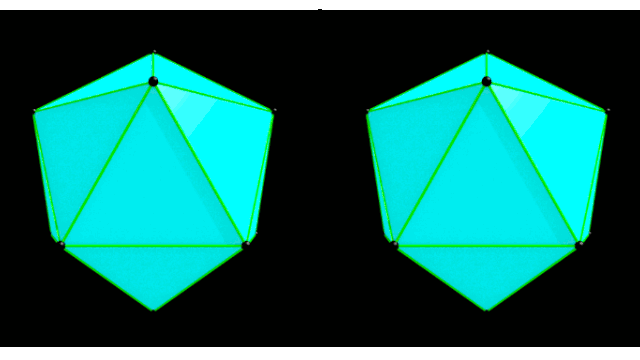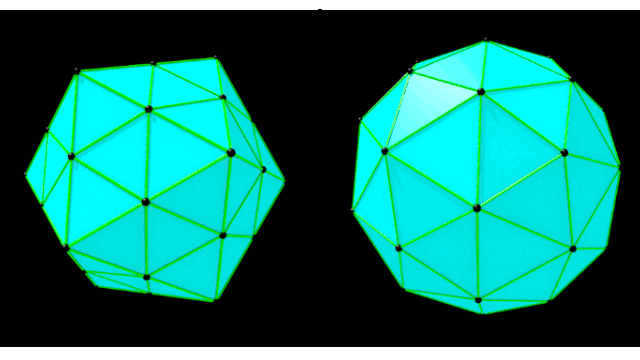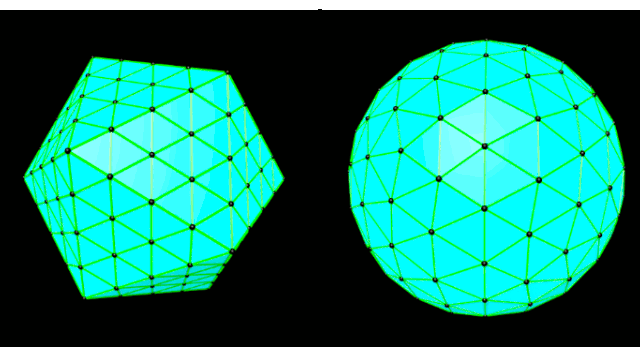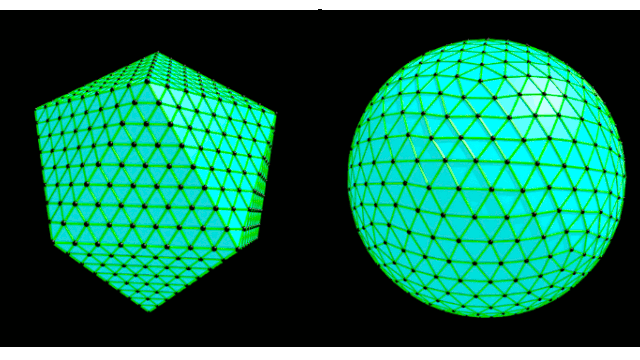
１．正二十面体を作る

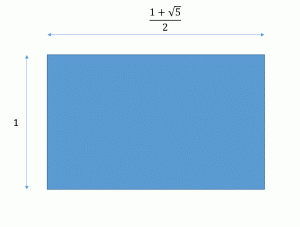
正二十面体は、1：( 1+ √5 ) / 2 の比率の長方形を立体的に三枚用意し、それぞれの頂点を正三角形になるように結ぶことで作成できる。

２．正二十面体の各三角形を再分割する

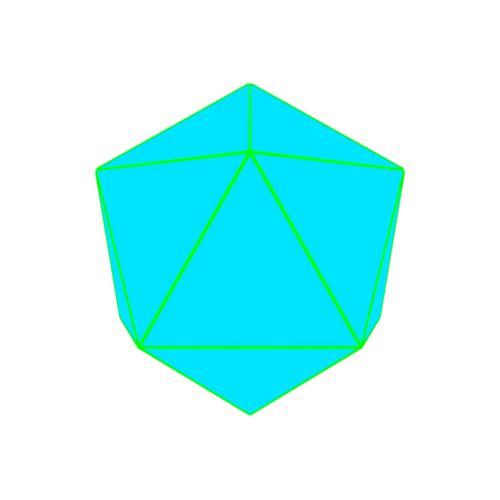
正二十面体の各三角形を４分割する。

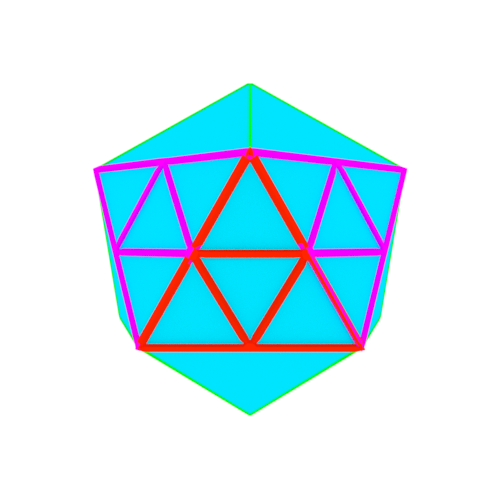
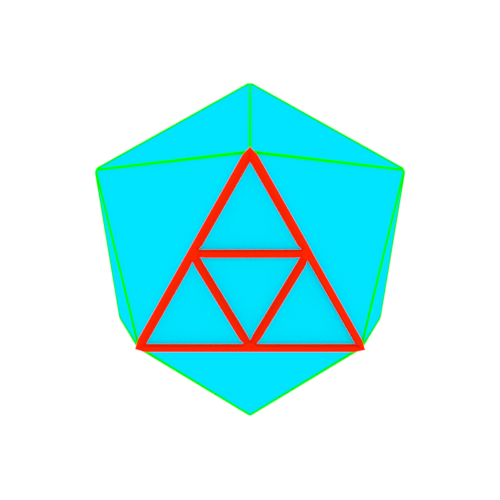
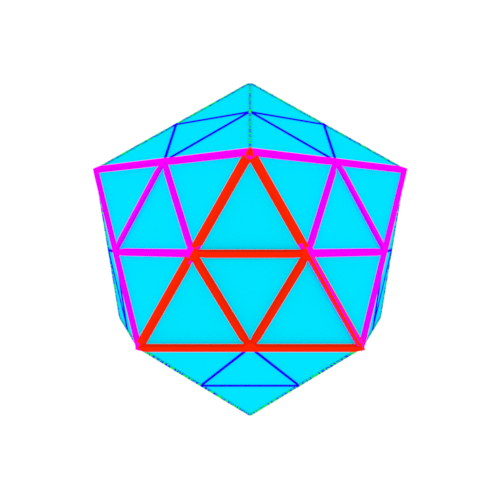
３．半径の再考と頂点の移動

このままでは球にならない。やりたいのは、分割してできた各頂点を球状に配置する事。

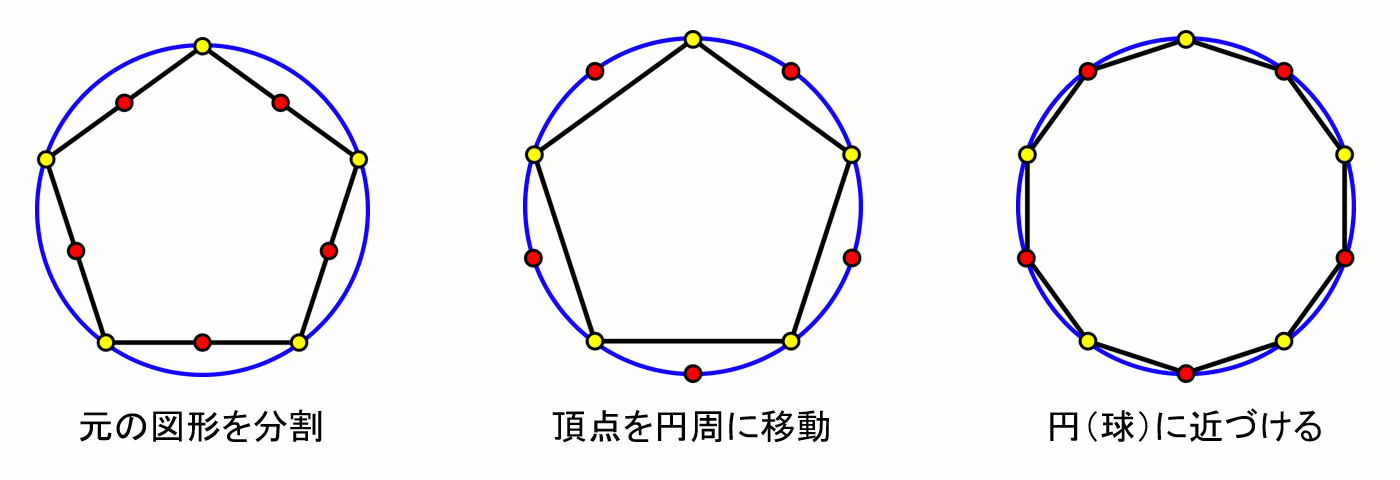
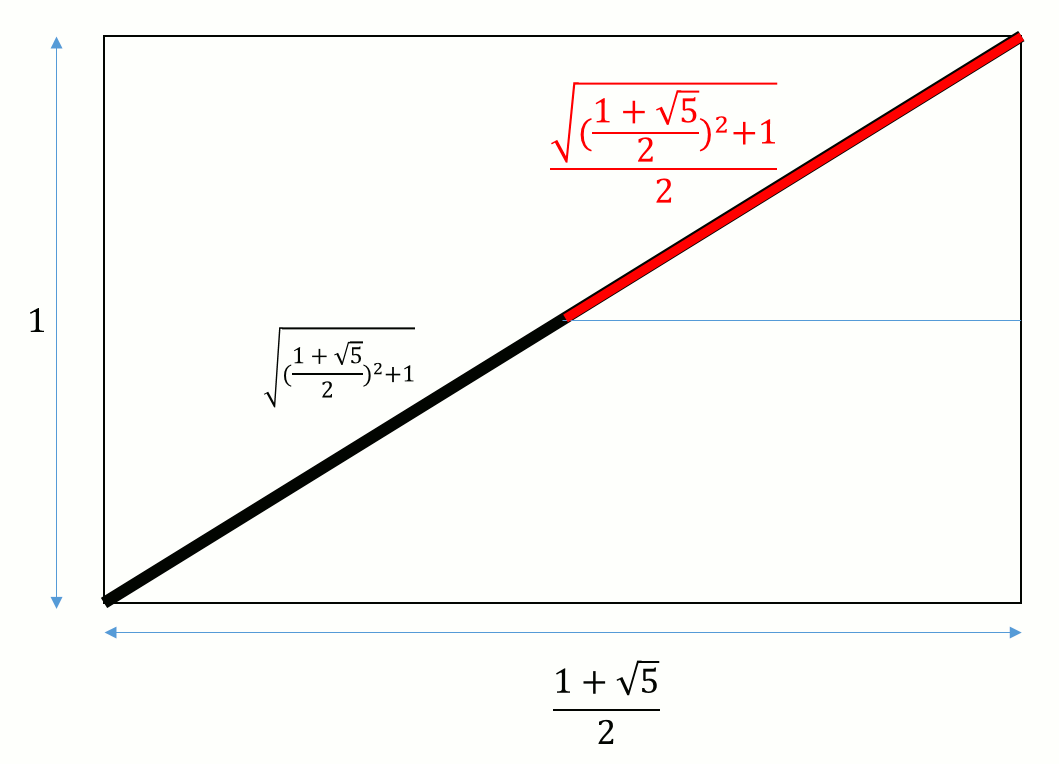
ここで、そもそもこの球の半径がいくつかを再考してみる。元々 1：( 1+ √5 ) / 2 の長方形の頂点からなる図形なので、半径はピタゴラスの定理から √(((1+√5)/2)^2+1)/2 が求まる。これでは使いにくい。

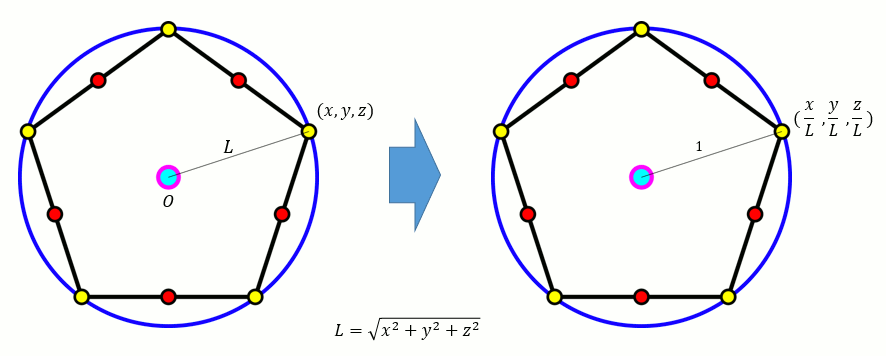
正攻法としては直径がdになるように辺の比率を調整する。半径１ならd=2とする。

実の所、正二十面体が求まった時点で、「原点→ある頂点」の位置ベクトルとして正規化してしまうのが手っ取り早いし後々も使える。 どうせ全ての頂点の「原点からの距離」はrで無ければならない。

次回はプログラムを書く

参考

Creating an icosphere mesh in code
http://blog.andreaskahler.com/2009/06/creating-icosphere-mesh-in-code.html

Weblog on mebius.tokaichiba.jp
http://ynomura.dip.jp/archives/2009/08/20.html

次の記事