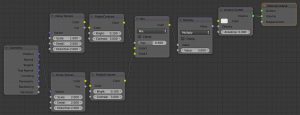
三次元オブジェクトをマウス回転(glut使用)
入門者がOpenGLを使う時、コードと出力結果だけでは何がどうなったのかわかりにくい事があります。
せめて回転ぐらいはしたいので、マウスの左ドラッグで描画対象を回転できるシンプルなコードを作成しました。
(例のごとく同種のものはいくらでもあると思います)
使い方:
マウス押下時に、dragstartを呼び出して回転開始を宣言します。
その後、マウスが動くたびにdragtoを呼び出して、回転状態を更新します。
最後、マウスボタンが離された時にdragendを呼び出して、回転の終了を宣言します。
球と直線の交差に関する式は
The Textbook of RayTracing @TDU
を参考にしました。
#pragma once #include <windows.h> #include <GL/gl.h> #include <GL/freeglut.h> #include "nurotate.h" #include "cube.h" int width, height; //回転オブジェクト定義 nu::mrotate camr; void disp(void) { glClear(GL_COLOR_BUFFER_BIT); glViewport(0, 0, width, height); glPushMatrix(); //原点を視線方向に0.5ずらす glTranslated(0, 0, -0.5); //回転行列を適用 double mat[16]; glMultMatrixd(camr.getmatrix(mat)); //一辺0.7のキューブを描画 cube(0.7); glPopMatrix(); glFlush(); } void reshape(int w, int h) { width = w; height = h; //クライアント領域のサイズを指定 //Win32APIの場合はGetClientRectで求めたrightとbottomだがglutではwとh camr.setWindowSize(width, height); //クライアント領域のどこの範囲に描画しているかを指定。 //glViewportで一画面丸々描画しているので、クライアント領域の(0,0)-(width,height)に書いていることになる camr.setRenderRect(0, 0, width, height); disp(); } //マウスクリック時のイベント void mouse(int button, int state, int x, int y) { if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) { camr.dragstart(x, y);//最初の回転軸を決定 } else if (state == GLUT_UP) { camr.dragend();//ドラッグ終了 } glutPostRedisplay(); } //ドラッグ時のイベント void motion(int x, int y) { camr.dragto(x, y);//移動中の回転軸を更新 disp(); } //エントリポイント int main(int argc, char ** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(400, 300); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("MouseRotateSample"); glutDisplayFunc(disp); glutReshapeFunc(reshape); glutMouseFunc(mouse); glutMotionFunc(motion); glutMainLoop(); return 0; }
呼出元のコードは見ての通りglutを使用していますが、freeglutを使っています。
また回転行列はglMultMatrixdで掛け合わせていますのでglRotate*等は使っていません。
#pragma once #include <cmath> namespace nu { //////////////////////////////////// //! @brief マウス回転用クラス class mrotate { double m_cam_matrix[16]; //!< @brief 現在の行列 double m_tmp_matrix[16]; //!< @brief マウス回転中に使用する一時的な行列 double m_vstart[3]; //!< @brief 回転スタート時の、「球の中心→"クリック位置のレイと球の交点"」 のベクトル double m_vend[3]; //!< @brief マウスが移動中の、〃 double m_raxis[3]; //vstartとvendの外積から算出した、回転中の回転軸(ベクトル) //viewportで指定した表示範囲をウィンドウ座標系で指定 int m_rectLTx, m_rectLTy; int m_rectRBx, m_rectRBy; //ウィンドウのサイズ int windowSizeX, windowSizeY; //マウスボタンが押されている間はtrueになり、trueの間は回転処理を行う bool m_fmousepush; public: mrotate(); ~mrotate(); //! @brief クライアント領域のサイズを指定する //! @param [in] width ウィンドウのクライアント領域の幅(ピクセル) //! @param [in] height ウィンドウのクライアント領域の高さ(ピクセル) void setWindowSize(const int width, const int height) { windowSizeX = width; windowSizeY = height; } //! @brief クライアント領域内にOpenGLで描画する範囲を矩形で指定。glviewportと同じだがこちらはクライアント座標系で矩形の四隅の座標を指定する void setRenderRect(int LeftTopX, int LeftTopY, int RightBottomX, int RightBottomY) { m_rectLTx = LeftTopX; m_rectLTy = LeftTopY; m_rectRBx = RightBottomX; m_rectRBy = RightBottomY; } //! @brief ドラッグ開始時に呼び出す //! @param [in] x クライアント座標系のマウスのx座標 //! @param [in] y クライアント座標系のマウスのy座標 //! @return なし void dragstart(int curx, int cury); //! @brief ドラッグ中に呼び出す //! @param [in] curx クライアント座標系のマウスのx座標 //! @param [in] cury クライアント座標系のマウスのy座標 //! @return なし void dragto(int curx, int cury); //! @brief ドラッグ終了時に呼び出す //! @return なし void dragend(); //! @brief 現在の回転行列を取得する const double* getmatrix(double* const dst)const; }; //////////////////////////////////// ///////////////////////////////////////////// //以下ベクトルと行列演算用の汎用的な関数//////// //三次元ベクトルの長さを求める inline double length3(const double* const vec3) { return std::sqrt(vec3[0] * vec3[0] + vec3[1] * vec3[1] + vec3[2] * vec3[2]); } //三次元ベクトルの外積を求める inline double inner3(const double * const vec1, const double * const vec2) { return ((vec1[0])*(vec2[0]) + (vec1[1])*(vec2[1]) + (vec1[2])*(vec2[2])); } inline void outer3(double * const dvec, double const * const svec1, double const * const svec2) { const double& x1 = svec1[0]; const double& y1 = svec1[1]; const double& z1 = svec1[2]; const double& x2 = svec2[0]; const double& y2 = svec2[1]; const double& z2 = svec2[2]; dvec[0] = static_cast<double>(y1 * z2 - z1 * y2); dvec[1] = static_cast<double>(z1 * x2 - x1 * z2); dvec[2] = static_cast<double>(x1 * y2 - y1 * x2); } inline double vangle3(double const * const vec1, double const * const vec2) { return acos(inner3(vec1, vec2) / (length3(vec1) * length3(vec2))); } inline void GetRotateMatrix(double* const m, const double radian, const double * const axis) { double s = sin(radian); double c = cos(radian); double len = length3(axis); double x = axis[0] / len; double y = axis[1] / len; double z = axis[2] / len; m[0] = x * x*(1 - c) + c; m[4] = x * y*(1 - c) - z * s; m[8] = x * z*(1 - c) + y * s; m[12] = 0; m[1] = x * y*(1 - c) + z * s; m[5] = y * y*(1 - c) + c; m[9] = y * z*(1 - c) - x * s; m[13] = 0; m[2] = x * z*(1 - c) - y * s; m[6] = y * z*(1 - c) + x * s; m[10] = z * z*(1 - c) + c; m[14] = 0; m[3] = 0; m[7] = 0; m[11] = 0; m[15] = 1; } inline bool normalize3(double * const pV) { double len; double& x = pV[0]; double& y = pV[1]; double& z = pV[2]; len = sqrt(x * x + y * y + z * z); if (len < 1e-6) return false; len = 1.0 / len; x *= len; y *= len; z *= len; return true; } inline double* CopyMat44(double* const dst16, const double* const src16) { for (int i = 0; i < 16; i++) { dst16[i] = src16[i]; } return dst16; } inline double* MultMatrix(double* const dst, const double* const m1, const double* const m2) { for (int i = 0; i < 16; i++) dst[i] = 0.0; double d1, d2; for (size_t j = 0; j < 4; j++) for (size_t k = 0; k < 4; k++) for (size_t c = 0; c < 4; c++) { d1 = m1[4 * j + c]; d2 = m2[4 * c + k]; dst[4 * j + k] += d1 * d2; } return dst; } inline double* MultMatrix(double* dst, const double* const src) { double m1[16]; for (int i = 0; i < 16; i++) { m1[i] = dst[i]; } MultMatrix(dst, m1, src); return dst; } inline void loadIdentity16(double * const mat) { for (int i = 0; i < 16; i++) { mat[i] = 0; } mat[0] = 1; mat[5] = 1; mat[10] = 1; mat[15] = 1; } }
前半はクラスの定義です。後半はベクトルや行列に関する演算用の汎用的な関数です。
#include "nurotate.h" #include <cstdio> namespace nu { mrotate::mrotate() { loadIdentity16(m_cam_matrix); loadIdentity16(m_tmp_matrix); m_fmousepush = false; } mrotate::~mrotate() { } const double* mrotate::getmatrix(double* const dst)const { CopyMat44(dst, m_cam_matrix); MultMatrix(dst, m_tmp_matrix); return dst; } void mrotate::dragstart(int curx, int cury) { //本来はマウスが押されている間に呼び出されることはない //もしそういうことが起こったら何もせずに抜ける if (m_fmousepush == true) return; //ドラッグ中であることを示す m_fmousepush = true; printf(" dragstart\n"); const long cx = (m_rectRBx - m_rectLTx) / 2;//開始点を左上と考えた時の、画面中央の座標 const long cy = (m_rectRBy - m_rectLTy) / 2;// const long x = curx - m_rectLTx - cx;//cx,cyを0と考えた時のマウスの座標(左下原点) const long y = (windowSizeY - cury) - m_rectLTy - cy; //球の半径 double r = std::fmin((m_rectRBx - m_rectLTx), (m_rectRBy - m_rectLTy)); //レイの方程式 p = s + td double s[3] = { (double)x,(double)y,-1000 }; double d[3] = { 0,0,1 }; double A = std::pow(length3(d), 2); double B = 2 * inner3(s, d); double C = std::pow(length3(s), 2) - r * r; double t1 = (-B + std::sqrt(B*B - 4 * A * C)) / (2 * A); double t2 = (-B - std::sqrt(B*B - 4 * A * C)) / (2 * A); //交点 double p[3] = { s[0] + t1 * d[0], s[1] + t1 * d[1], s[2] + t1 * d[2] }; normalize3(p); //中心→交点のベクトル m_vstart[0] = p[0]; m_vstart[1] = p[1]; m_vstart[2] = p[2]; } void mrotate::dragto(int curx, int cury) { //マウスドラッグ中でないなら何もしない if (m_fmousepush == false) return; printf(" dragend\n"); const long cx = (m_rectRBx - m_rectLTx) / 2;//開始点を左上と考えた時の、画面中央の座標 const long cy = (m_rectRBy - m_rectLTy) / 2;// const long x = curx - m_rectLTx - cx;//cx,cyを0と考えた時のマウスの座標(左下原点) const long y = (windowSizeY - cury) - m_rectLTy - cy; //球の半径 double r = std::fmin((m_rectRBx - m_rectLTx), (m_rectRBy - m_rectLTy)); //レイの方程式 p = s + td double s[3] = { (double)x,(double)y,-1000 }; double d[3] = { 0,0,1 }; double A = std::pow(length3(d), 2); double B = 2 * inner3(s, d); double C = std::pow(length3(s), 2) - r * r; double t1 = (-B + std::sqrt(B*B - 4 * A * C)) / (2 * A); double t2 = (-B - std::sqrt(B*B - 4 * A * C)) / (2 * A); //交点 double p[3] = { s[0] + t1 * d[0], s[1] + t1 * d[1], s[2] + t1 * d[2] }; normalize3(p); //中心→交点のベクトル m_vend[0] = p[0]; m_vend[1] = p[1]; m_vend[2] = p[2]; outer3(m_raxis, m_vstart, m_vend); normalize3(m_raxis); double angle = vangle3(m_vstart, m_vend) * 3; if (abs(angle) < 1e-6) return; GetRotateMatrix(m_tmp_matrix, angle, m_raxis); } void mrotate::dragend() { //マウスが押されている間しか処理しない if (m_fmousepush == false) return; //マウスドラッグが終わったことを示す m_fmousepush = false; MultMatrix(m_cam_matrix, m_tmp_matrix); loadIdentity16(m_tmp_matrix); } }
クラスの実装です。
Blender bpy で各データへアクセス
調査中のメモです。
1.現在アクティブなオブジェクトへアクセス
import bpy; print ( bpy.context.active_object )
「アクティブなオブジェクト」というのはオレンジ色で強調されているもののことで、複数選択されているときも、アクティブなオブジェクトは一つだけです。
2.現在選択中のオブジェクトへアクセス
2.1 選択中のオブジェクトを列挙
import bpy; print ( bpy.context.selected_objects )
結果出力
2.2 選択中のオブジェクトの個数を取得
import bpy; print ( len(bpy.context.selected_objects) )
結果出力
3.オブジェクトの頂点へアクセス
3.1 オブジェクトの頂点の個数を取得
import bpy; print( len(bpy.context.active_object.data.vertices) )
結果出力
3.2 オブジェクトの頂点の座標を取得
import bpy; print( bpy.context.active_object.data.vertices[0].co )
結果出力
4.オブジェクトのエッジへアクセス
4.1 オブジェクトのエッジの個数を取得
import bpy; print( len(bpy.context.active_object.data.edges) )
結果出力
4.2 あるエッジを構成する頂点のインデクスを取得
import bpy; print( "vtx1 : " , bpy.context.active_object.data.edges[1].vertices[0] ) print( "vtx2 : " , bpy.context.active_object.data.edges[1].vertices[1] )
結果出力
vtx2 : 3
4.3 あるエッジを構成する頂点のインデクスから各座標を取得する
import bpy; print( "vtx1 : " , bpy.context.active_object.data.vertices[ bpy.context.active_object.data.edges[1].vertices[0] ].co ) print( "vtx2 : " , bpy.context.active_object.data.vertices[ bpy.context.active_object.data.edges[1].vertices[1] ].co )
結果出力
vtx2 : <Vector (-1.0000, 1.0000, -1.0000)>
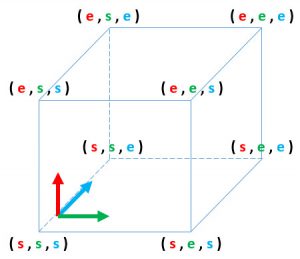
glutのマウス操作
GLUTでのマウス操作一覧です。
#include <Windows.h> #include <gl/GL.h> #include <gl/freeglut.h> #pragma comment(lib,"opengl32.lib") #pragma comment(lib,"freeglut.lib") void disp(void) {} void mouse(int button, int state, int x, int y) { if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) { printf("left button down\n");//左ボタンダウン } if (button == GLUT_LEFT_BUTTON && state == GLUT_UP) { printf("left button up\n");//左ボタンアップ } if (button == GLUT_RIGHT_BUTTON && state == GLUT_DOWN) { printf("right button down\n");//右ボタンダウン } if (button == GLUT_RIGHT_BUTTON && state == GLUT_UP) { printf("right button up\n");//右ボタンアップ } if (button == GLUT_MIDDLE_BUTTON && state == GLUT_DOWN) { printf("middle button down\n");//中ボタンダウン } if (button == GLUT_MIDDLE_BUTTON && state == GLUT_UP) { printf("middle button up\n");//中ボタンアップ } } //ドラッグ void motion(int x, int y) { printf("drag ... %d %d\n",x,y); } //ホイール void mouseWheel(int button, int dir, int x, int y) { if (dir > 0) { printf("wheel up\n"); } else { printf("wheel down\n"); } return; } int main(int argc,char** argv) { glutInit(&argc, argv); glutInitWindowPosition(100, 50); glutInitWindowSize(400, 300); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA); glutCreateWindow("mouse demo"); glutDisplayFunc(disp); glutMouseFunc(mouse); glutMotionFunc(motion); glutMouseWheelFunc(mouseWheel); glutMainLoop(); return 0; }
Blender pythonでノードにキーフレームを追加
Vray for blenderのノードにキーフレームを追加する作業は、値をポイントして[i]キーを押せば良いです(つまり普通のキーフレーム追加作業)。
しかしなぜかDopeSheetやGraphEditorで表示されないため、変化速度のカーブを編集したりできません。
仕方が無いので、pythonで1フレームずつ設定します。
1.設定したい項目をポイントし、pythonからのアクセス方法を確認します。
2.この情報を使って、以下のコードを作成します
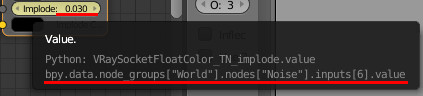
import bpy for i in range(1,1000): bpy.context.scene.frame_set(i) bpy.data.node_groups["World"].nodes["Noise"].inputs[6].value=i/1000 bpy.data.node_groups["World"].nodes["Noise"].inputs[6].keyframe_insert('value',frame=i)
※ bpy.context.scene.frame_set(i)
現在のフレームをiに設定します
※keyframe_insert
その項目にキーフレームを挿入します
frame=iは挿入するフレーム番号ですが、省略すると現在のフレームに挿入されます。従って先にframe_setをしてあるこの例では以下のように書いても動作します。
bpy.data.node_groups["World"].nodes["Noise"].inputs[6].keyframe_insert('value')
なお、下のようにして現在のキーフレームを取得できます
参考:
(Blender) (Python)How can I animate the factor value in the mix node with Python code?
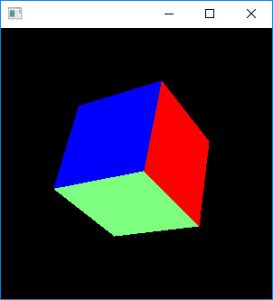
OpenGLでCubeを描く関数
希にほしくなるCubeを描画する関数です。同種の物は探せばいくらでも出てくると思います。
OpenGLはデフォルトで反時計回りを面の表としているので、glFrontFace(GL_CCW)でカリングをし、面の向きが全てCubeの外側を向いていることを確認しています。実際に使用するときは外すと良いと思います。
//! @brief 立方体を描画 //! @param [in] width 立方体の一辺の長さ //! @return なし void cube(double width) { double ws = -width / 2; double we = width / 2; double xs = ws; double ys = ws; double zs = ws; double xe = we; double ye = we; double ze = we; glFrontFace(GL_CCW);//反時計回りが表 glEnable(GL_CULL_FACE);//カリングを有効にする glBegin(GL_QUADS); glColor3d(0.5, 0.5, 1.0); glVertex3d(xs, ys, zs);// glVertex3d(xs, ye, zs); glVertex3d(xe, ye, zs); glVertex3d(xe, ys, zs); glColor3d(0.0, 0.0, 1.0); glVertex3d(xs, ye, ze);// glVertex3d(xs, ys, ze); glVertex3d(xe, ys, ze); glVertex3d(xe, ye, ze); glColor3d(0.0, 0.5, 0.0); glVertex3d(xs, ye, zs);// glVertex3d(xs, ye, ze); glVertex3d(xe, ye, ze); glVertex3d(xe, ye, zs); glColor3d(0.5, 1.0, 0.5); glVertex3d(xs, ys, zs);// glVertex3d(xe, ys, zs); glVertex3d(xe, ys, ze); glVertex3d(xs, ys, ze); glColor3d(1.0, 0.5, 0.5); glVertex3d(xs, ys, zs);// glVertex3d(xs, ys, ze); glVertex3d(xs, ye, ze); glVertex3d(xs, ye, zs); glColor3d(1.0, 0.0, 0.0); glVertex3d(xe, ys, zs);// glVertex3d(xe, ye, zs); glVertex3d(xe, ye, ze); glVertex3d(xe, ys, ze); glEnd(); glDisable(GL_CULL_FACE);//カリングを無効にする }
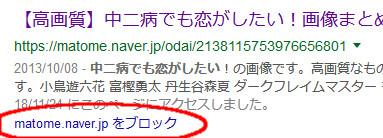
googleの検索結果からキュレーションサイトを排除する
NAVERまとめを除外したいんです。
それはもう、切実に。
Naverまとめは便利だ。芸能人のゴシップとか本来知る必要すらないような情報を検索して、信憑性のない断片的な情報から想像を膨らませて楽しむには最適と言える。
勿論、今夜のおかずを何にするかと言った、重要な決定をするときには使えない。信憑性、可読性、独自性、そして情報量において他メディアに比べ圧倒的に劣っているからだ。
だが問題は、にもかかわらず、google検索で上位に表示される点にある。
PersonalBlocklist
キュレーションサイトを検索結果から外すには、Personal Blocklistプラグインを使います。Firefox用、Chrome用があります。
Chrome用 ... Chrome ウェブストア Personal Blocklist (by Google)
Firefox用 ... Personal Blocklist (not by Google)
Firefox用で説明します。インストールするとブラウザ右上に赤いボタンが出ます。
この状態で普通に検索すると、検索結果の左下に「xxxxx.comをブロック」という項目が出てきます。これをクリックすると以降、検索結果にこのドメインのサイトが表示されなくなります。
ページ単位でなくサイト単位で表示されなくなるので、1クリックでまとめサイトを丸ごと一つ排除出来ます。
なお、ブロックを解除したいときは、先の右上の赤いボタンをクリックし、「ブロックの解除」をクリックします。
uBlacklist
ただし、2018/11/28現在、Chrome用のほうが全く機能しないようです。「ブロックするための項目がサイト名付近から消える」というトラブルは過去にも数回起こっているようですが、少なくとも私の環境では一切の動作をしませんでした。代替として、Chrome用にはuBlacklistがあります。
uBlacklistの場合、一度そのサイトに入る必要があります。まとめサイトに入った上で、ブラウザ右上にある禁止マークをクリックし、「このサイトをブロックする」と表示された状態でOKボタンを押します。
以下、雑談
まとめサイトの事を正確には「キュレーションサイト」といいます。
キュレーションサイト自体は本来悪い物ではないのですが、最新のSEOを徹底的に施した粗悪なコピペ記事の量産により、検索結果がゴミサイトばかりになるという事で、キュレーション汚染とまで言われています。
なぜそうなるかというと「クラウドソーシング」と呼ばれる、オンラインで個人に仕事を依頼する方法で、1記事100円等という低予算でど素人によるGoogle検索結果のコピペ作業で完成したページだからです。
広告収入を目的に記事を書くのは良いと思います。品質を保つには予算かモチベーションの少なくともどちらか一方は必ず必要です。問題は品質が保てていないことです。Googleは検索アルゴリズムの変更で対処するようですが、もういっそ営業妨害で訴えたらどうか。
ちなみに私がなぜ今頃キレたかというと、諸事情により中二病の壁紙を検索したら頭のほうをnaverが独占したからです。
壁紙は壁紙サイト自体がまとめサイトみたいな物です。まとめをまとめるとかもう訳がわかりません。
Blenderで雲を作るチュートリアルを試す(8)
Clouds Tutorial for Blender Cycles
前回までで基本は完了となる。
あとはイメージ通りの風景にするための微調整として、様々な位置に雲を追加していく。
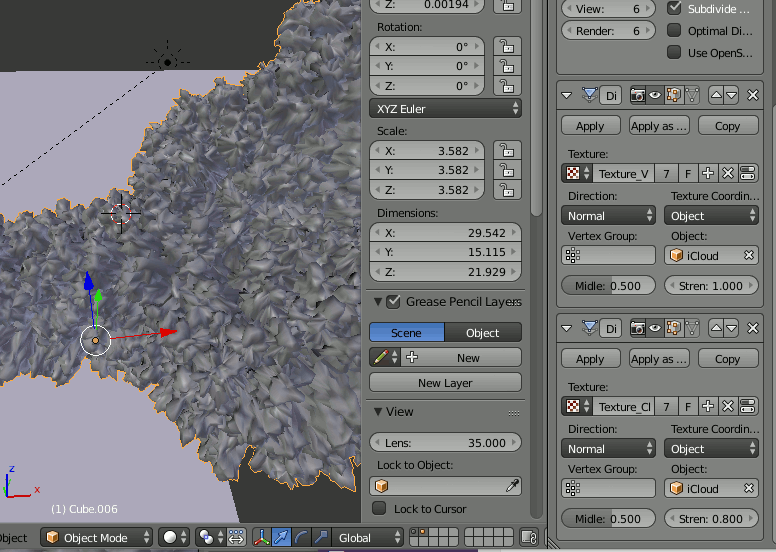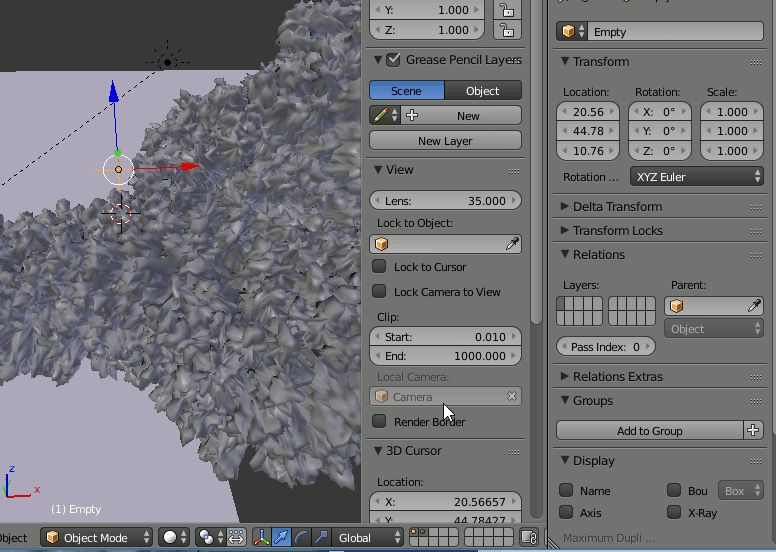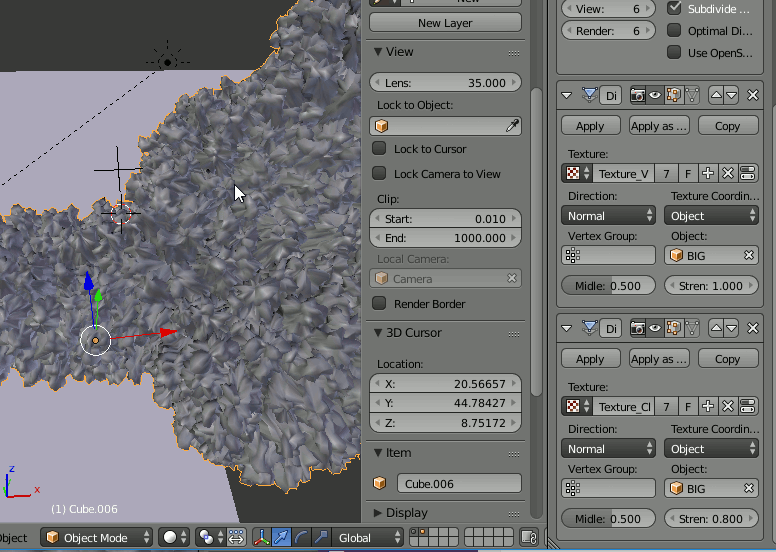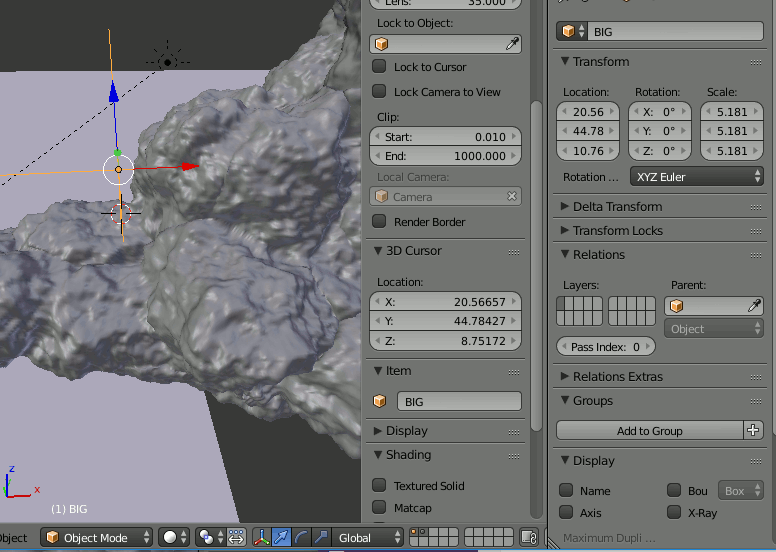
既存の雲を[Shift+D]でコピーした場合はマテリアルも複製されているので、Displaceのテクスチャを状況に応じてiCloudをつかうかBIGを使うかを選択すると良い。
新しく雲を作成した場合、既存の雲と同時に選択し、Ctrl+LでMaterialモディファイアをMake Linkすることで、此までと同じ設定をする手間を省くことができる。
さらに、雲のマテリアルを数種類追加する。
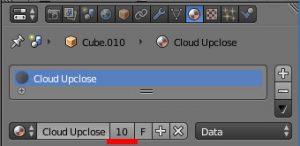
マテリアルを追加するとき、全く違うマテリアルなら新規作成するが、今回のように現在のマテリアルを修正する場合、既存のマテリアルが有効な状態で、マテリアル名横の数字をクリックすることで、既存のマテリアルをコピーできる。
この数字は、現在選択中のオブジェクトが使用しているマテリアルは、何個のオブジェクトと共有されているかという意味である。この数字をクリックするとマテリアルがコピーされ、新たなマテリアルは現在のオブジェクトだけが使用する状態になる。
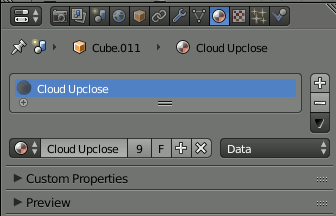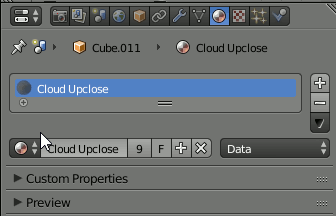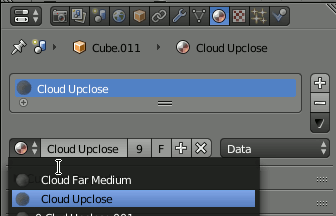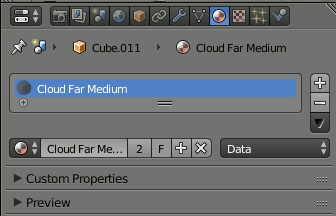
逆に、コピーしたオブジェクトにはCloud Upcloseが適用されているはずだが、これを先ほど作ったCloud Far Mediumに変更したい場合、マテリアルのリストから既存のマテリアルを選択する。
[52:19 命名] Cloud Upclose (Viewport色 明るい灰色) (このcloseは近くの意味)
[53:01 追加] Cloud Far Medium (Viewport色 灰色)
[53:37 追加] Cloud Far Heavy (Viewport色 暗い灰色)
このようにしてマテリアルと形状を組み合わせた雲を配置する。
これは自分の好みの問題なので、より動画に忠実に配置したい人は動画の[50:30~]を見てほしい。英語だが、動きだけ見ていれば何をしているのかはわかる。
ここまでの結果。背景を透過したPNG版だと特にわかりにくいが、volumeのアーティファクトが沢山できている。動画ではBlenderで対処せず、Photoshopなどのフォトレタッチソフトで修正をかけている。
Blenderで雲を作るチュートリアルを試す(7)
Clouds Tutorial for Blender Cycles
[38:30~ ]
眼下の一面の雲のモデリングが終わったので、両脇の雲を別に作成する。
その前に、前回まで作成した各モデルのモディファイアを不可視にし、モデリング中の表示速度を改善する。
[38:55~ ]
Blenderで雲を作るチュートリアルを試す(4)![]() と同じ方法で、新しい雲を作る。
と同じ方法で、新しい雲を作る。
できたら、それをカメラの目の前に配置する。
[41:55~ ]
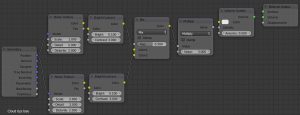
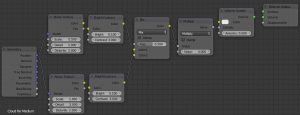
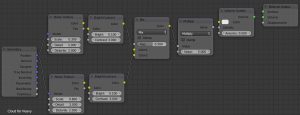
そして、追加した雲のマテリアルを設定する。
- ① [Shift+A]→[Input]→Geometry (Position→②Vector,③Vector)
- ② [Shift+A]→[Texture]→[Noise Texture] (Fac→④Color)
Scale=1.0 ,Detail=2.0 ,Distortion=2.0 - ③ [Shift+A]→[Texture]→[Noise Texture] (Fac→⑤Color)
Scale=2.0 ,Detail=2.0 ,Distortion=2.0 - ④ [Shift+A]→[Color]→[Bright Contrast] (Color→⑥Color1)
Bright=0.1 , Contrast=3.0 - ⑤ [Shift+A]→[Color]→[Bright Contrast] (Color→⑥Color2)
Bright=0.1 , Contrast=3.0 - ⑥ [Shift+A]→[Color]→[MixRGB] (Color→⑦Value(上))
Fac=0.5 - ⑦ [Shift+A]→[Converter]→[Math] (Value→⑧Density)
Multiply , Value(上)=⑦ , Value(下)=3.0 - ⑧ [Shift+A]→[Shader]→[Volume Scatter] (Volume→Material Ooutput)
Density=⑦
さらに以下の形状の雲を作り、カメラから少し遠いところに配置する。
このとき、カメラから離れたところに配置すると小さく見えるので、モデルを[S]で拡大する。しかし、拡大するとスケーリングが変化し、ノイズが尖ってしまう。
そのために、新たにEmpty(名前をBIGとする)を追加し、このオブジェクトにかかっているDisplaceモディファイアに指定されている[Texture Coordinate]→[Object]にBIGを指定する。そしてBIGを拡大、縮小し、適切なノイズに調整する。
この作業はBlenderで雲を作るチュートリアルを試す(4)![]() で行ったのと同じ内容である。
で行ったのと同じ内容である。
Blenderで雲を作るチュートリアルを試す(6)
Clouds Tutorial for Blender Cycles
[34:20~ ]
マテリアルの設定に入る。
ただし、動画とは若干前後するが、先にレンダリングの設定を行っておく。
Renderを開き、
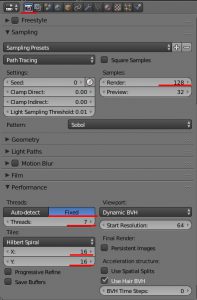
[Sampling]→[Samples]→Render=30
(※ 動画では、最低30、と言っている)
[Performance]→[Tiles]→X=16,Y=16
[Performance]→[Thread]→Fixed
[Performance]→[Thread]→Threads=7
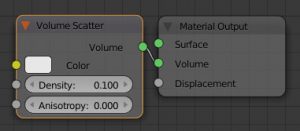
前々回作った"iCloud"の雲のオブジェクトを一つ選択し、マテリアルを追加後、以下のようにノードを設定する。
{Volume Scatter (Density:0.1)}
→[Volume]{Material Output}
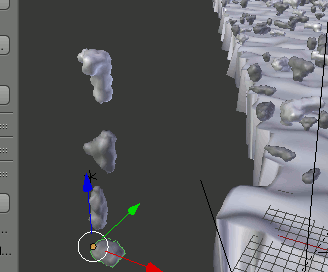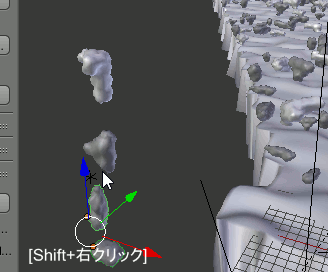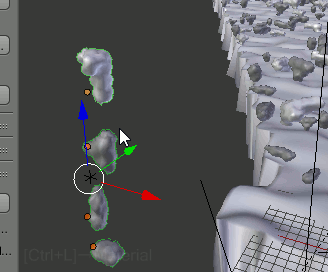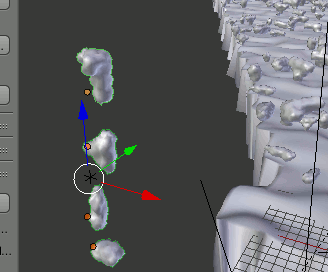
iCloudグループの全ての雲にこの設定を適用するため、Shift+右クリックでiCloudグループの全てのオブジェクトを選択し、Ctrl+L→[Make Links]→Materialを実行する。
このとき、先にマテリアルを追加しておいたオブジェクトを最後に選択することに注意する。
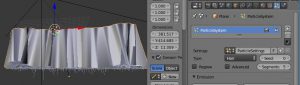
ここまでのレンダリング結果
この結果の中で、雲の形状の周辺に黒い部分(アーティファクト)が生じている。これは透過PNGを複数重ねたときにも生じる、Cyclesの透過の回数制限が原因である。
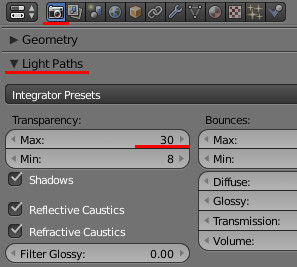
解決するため、Renderへ行き、
[Light Path]→[Transparency]→Max=30
を設定する。
ここまでのレンダリング結果(Light Path変更後)
Blenderで雲を作るチュートリアルを試す(5)
Clouds Tutorial for Blender Cycles
面状の雲に、小さな雲を配置していく。
[32:00~ ]
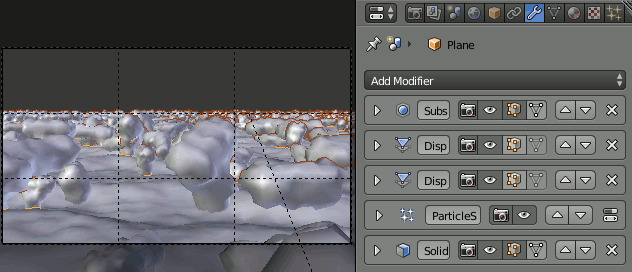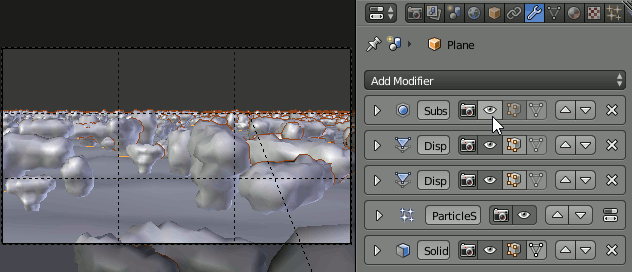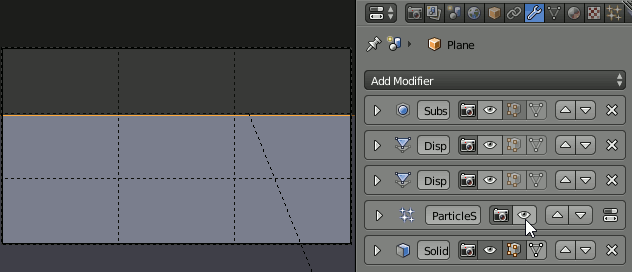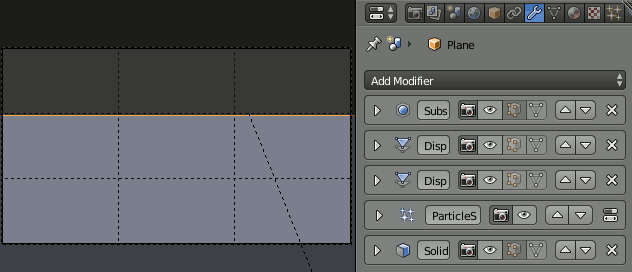
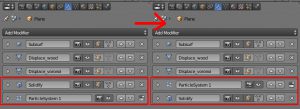
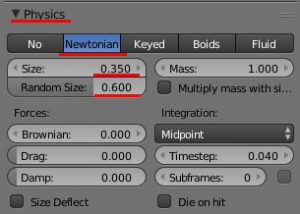
面状の雲にHair Particleを追加する。
このとき、Hairが雲の裏側に出る。これはSolidifyモディファイアの後にParticleを発生させているためである。回避するために、モディファイアの適用順序を、Particle→Solidifyに変更する。
Hair ParticleのAdvancedをチェックし、
[33:00~ ]
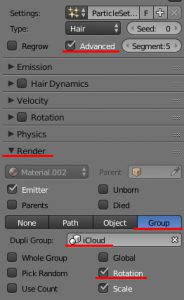
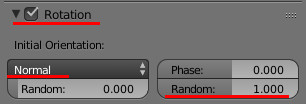
動画と前後するが、最後に回転を設定する。
まず、BlenderのParticleでオブジェクトを指定すると(なぜか)90度反転するので、オブジェクトをY軸に-90度回転する。
その後、
- [Rotation]→[Initial Orientaion]→Normal
- Phase下Random=1.0 ※
※このRandomは、動画では1.0が最大になっているが、筆者の環境Blender2.79では最大2.0になっていた。
ここまでの結果