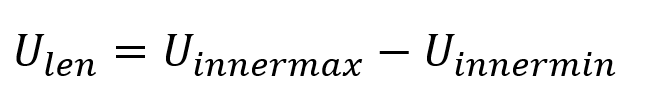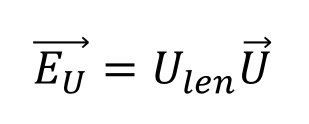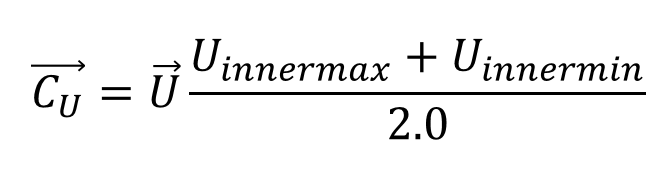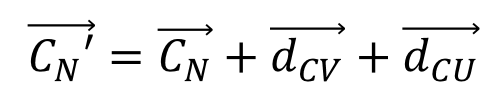<<前の記事 次の記事>> | キーワード：C/C++

2020年8月30日公開
2020年8月30日

OBBとAABB

OBBは物体を最小で囲むBoundingBoxの事で、無駄なく囲めるが求めるのが難しい。

AABBは物体のX軸Y軸Z軸の最大-最小からなるBoundingBoxで、求めるのがきわめて簡単だが無駄が多い。

主成分分析

以前、主成分分析で点群の法線を求めた。三次元の点群に主成分分析をかけた結果出てきた第一、第二、第三主成分を使えばOBBが求められる。

主成分分析で三次元点群から平面を求める – 1 – 分散共分散行列を求める

主成分分析で三次元点群から平面を求める – 2 – 固有ベクトルを求める

参考文献

以下のサイトをなぞっていく。

http://www.nomuraz.com/denpa/prog005.htm

手順

①　OBBの各辺の方向を求める

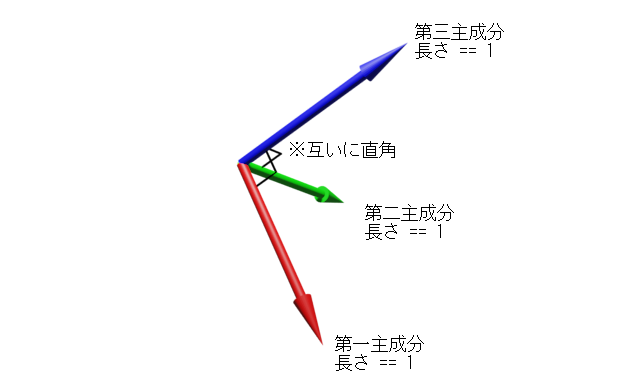
三次元点群データを主成分分析すると、固有ベクトルが三つ（第一、第二、第三主成分）得られる。

この三つのベクトルは互いに垂直で且つ長さが１になっている。

この各ベクトルが、OBBの各辺の方向となる。

つまり、各辺の方向は主成分分析の結果そのものである。

面の抽出の時は広がりの一番小さい方向を表す第三主成分を使ったがOBBの時は三つとも使うことになる。

以下、各ベクトルを→U , →V , →N とする。

②　OBBの各辺の長さ

方向がわかったので次は辺の長さを求める。

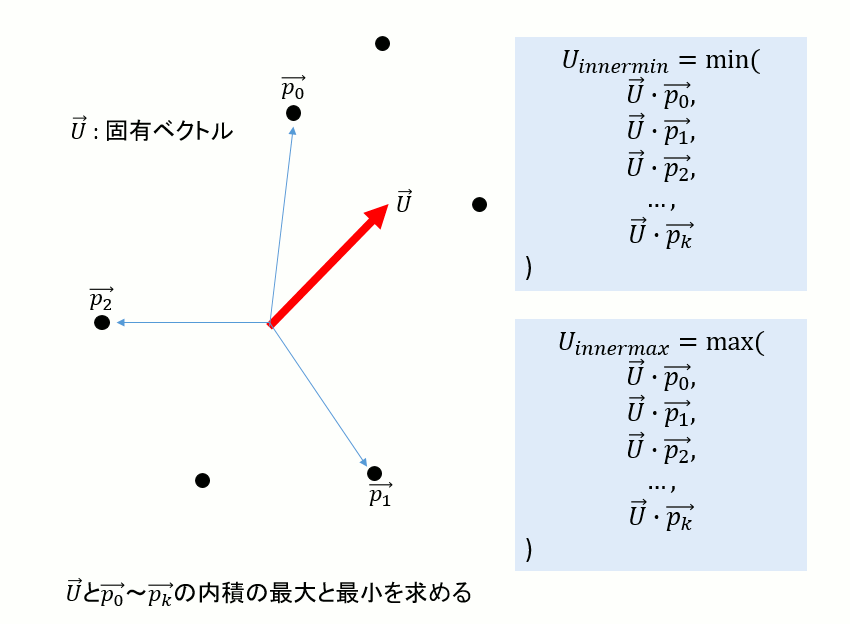
まず、固有ベクトルについて、そのベクトルとすべての頂点座標（位置ベクトル）の内積をとり、その最大・最小を求める。

こうして求めたU,V,Nの(max-min)の値が、各方向の辺の長さとなる

この計算を、→U , →V , →N それぞれについて行う。

そして、OBBの辺としての長さがわかったので、各辺をベクトルで表すと、

これでエッジの長さと方向を表す→EU , →EV , →ENが求められた。

③　OBBの各辺の中央

各内積の最大と最小を足して２で割り、各ベクトルを掛けると、各辺の中央が求められる

この計算も、→U , →V , →N それぞれについて行う。

これを→CU , →CV , →CNとする。

④　OBBの中央の算出

UV平面上の中央を求める

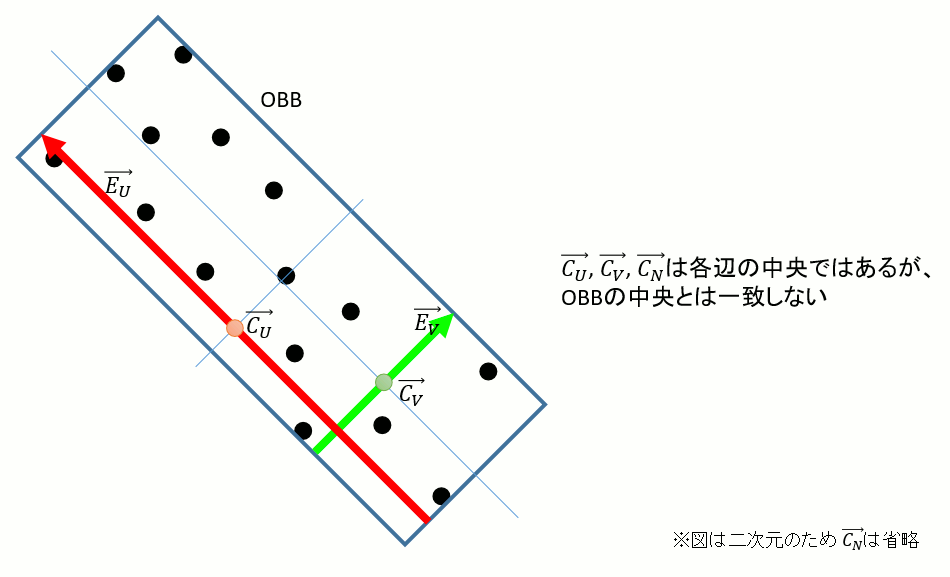
ここまでが上記参考文献の範疇なのだが、この→CU , →CV , →CN、実は一致しない。どうやら各辺の中央ではあるがボックスの中央ではないらしい。つまり以下のような関係になっていて、このまま辺の中央を使うわけにはいかない。

→U,→V,→N,→EU,→EV,→EN,→CU,→CV,→CN,からどうやってOBBの中央を求めればよいか。

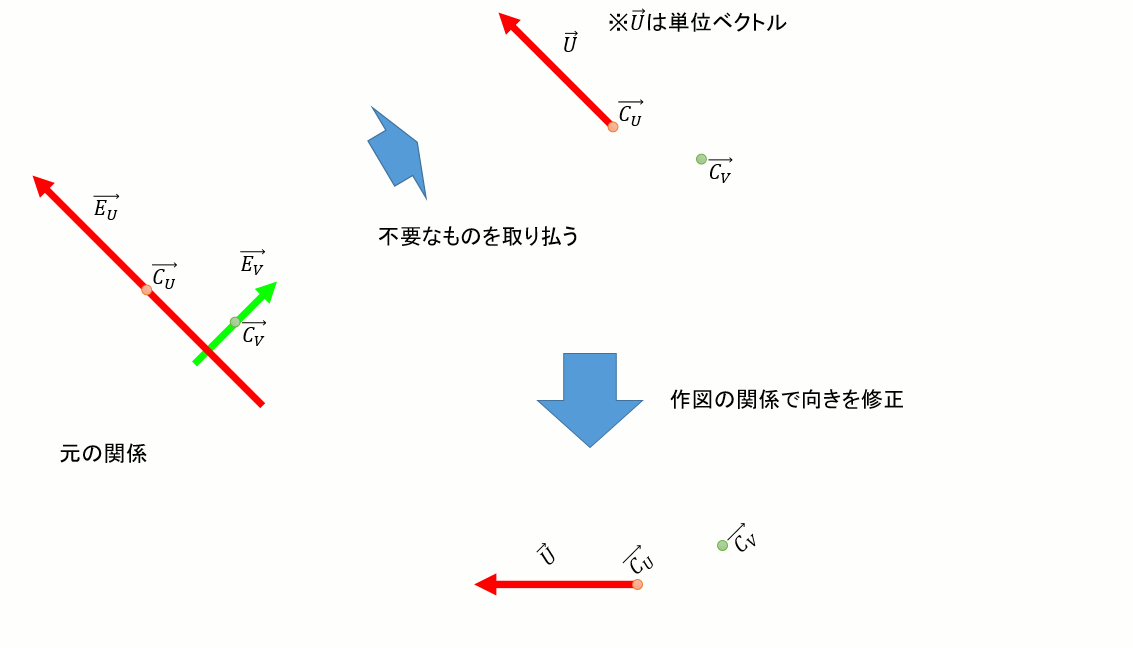
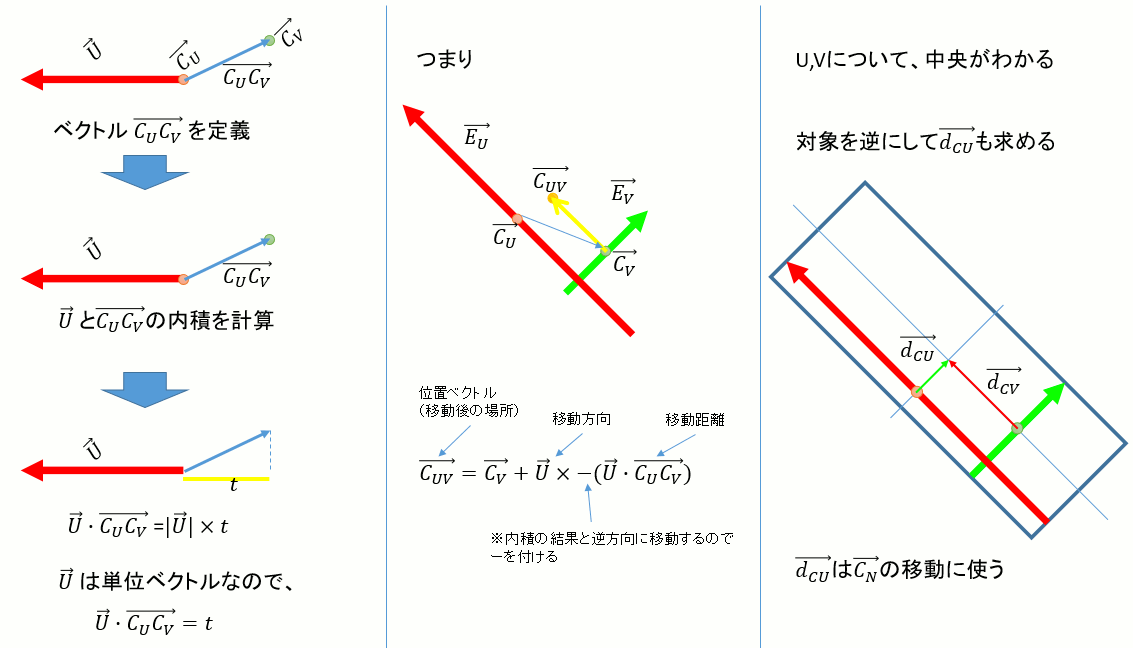
以下のように、内積を使って移動量と方向を表す→dCU,→dCVを求める。

→CVに→dCVを加えるか、あるいは→CUに→dCUを加えれば、UV平面上のOBBの中央が求まる。

なんでこれで求まるのかは以下を参照：

https://www.studyplus.jp/467
【内積とは】ベクトルの内積の意味や公式・計算方法を知って大学合格へ！

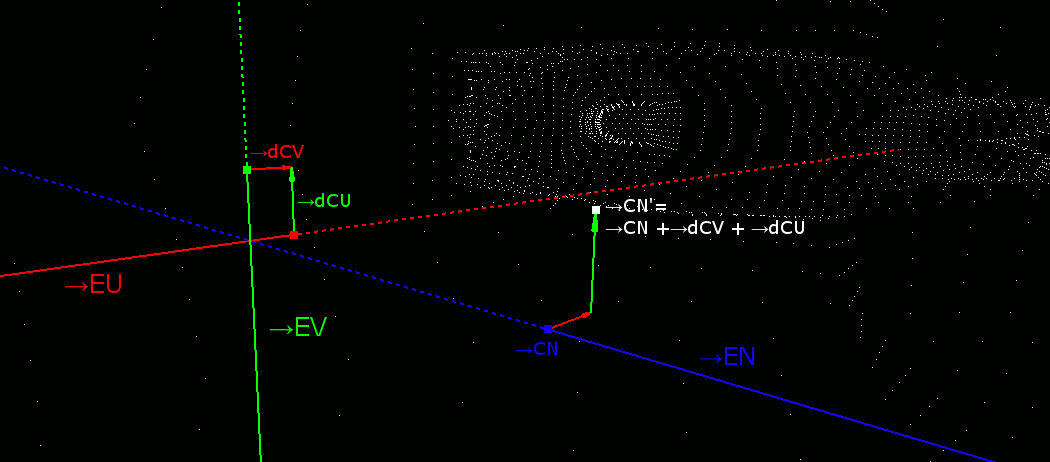
→CNを移動する

大変恐縮だが作図がもうめんどくさすぎるのでプログラムのSSで勘弁して欲しい。→CNの移動は、→CN' = →CN + →dCU+ →dCVとなる。

つまり、先ほどずっと計算していたUV平面と平行に移動する。

これでOBBの中央が求まった。

ＯＢＢの描画

ＯＢＢの中央が求まったら、そこから各方向の辺のベクトルの1/2を引けばＯＢＢの端の点が求められる。

ソースコード

疲れたので次回。