主成分分析(PCA)の前にデータを標準化する（Eigenライブラリ版）

2022年9月4日公開
2022年9月4日更新

C++のEigenライブラリで標準化までやってみる。本当はPCAもやりたいしEigenSolverを使えばいい事まではわかっているが結果の確認ができないので今はやらない。

#include <iostream>
#include <vector>
#include <Eigen/Dense>

int main()
{
  std::vector<std::array<float, 3> > cloud;
  cloud.push_back({ -1.841658711, 0.324050009, 1.041258931 });
  cloud.push_back({-1.449076772, 0.431593835, 0.987673104 });
  cloud.push_back({-1.04681015, 0.415599823, 1.049820662 });
  cloud.push_back({-0.646572888, 0.42549479, 1.087714672 });
  cloud.push_back({-0.25920701, 0.599574149, 0.971796691 });
  cloud.push_back({0.149769783, 0.497985959, 1.114130974 });
  cloud.push_back({-1.883069754, 0.6849733, 1.249212146 });
  cloud.push_back({-1.481496215, 0.677821219, 1.303076267 });
  cloud.push_back({-1.083532453, 0.716715276, 1.313803315 });

  Eigen::MatrixXf mat(9,3);
  for (size_t i = 0; i < cloud.size();i++) {
    mat.row(i) << cloud[i][0] , cloud[i][1] , cloud[i][2];
  }

  // センタリングしたデータを作成
  Eigen::MatrixXf centered = mat.rowwise() - mat.colwise().mean();

  std::cout << "---" << std::endl;

  // センタリングされたデータに対して、列ごとに標準偏差を求め、各列の要素を標準偏差で割る
  for (int c = 0; c < 3; c++) {
    auto col = mat.col(c).array();
    double std_dev = sqrt((col - col.mean()).square().sum() / col.size());
    centered.col(c) /= std_dev;
  }

  
  std::cout << std::endl << centered << std::endl;// 表示
  std::cout << std::endl << std::endl;

  //////////////////////
  // 分散共分散行列
  Eigen::MatrixXf cov = (centered.adjoint() * centered) / double(centered.rows());

  std::cout << cov << std::endl;// 表示
  return 0;


}

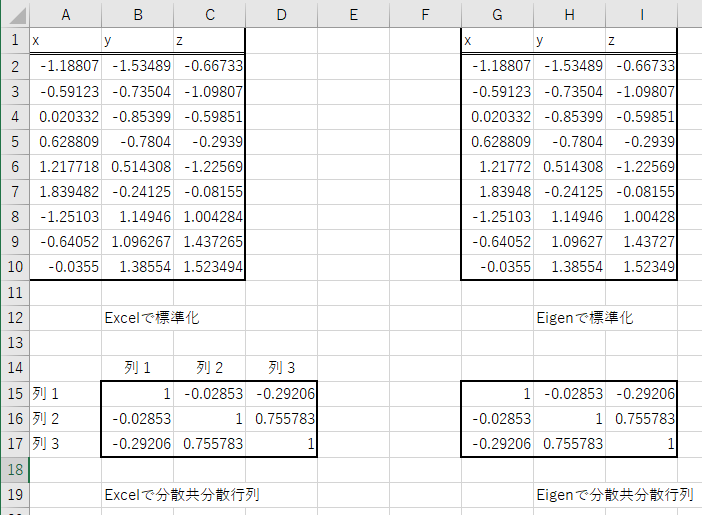
計算結果

Excelと同じ結果が出ている。

解説

センタリング

データのセンタリングは、データの平均値を０にすることなので、全てのデータから平均値を引けばよい。

rowwise()-colwise().mean()で行える。

  // センタリングしたデータを作成
  Eigen::MatrixXf centered = mat.rowwise() - mat.colwise().mean();

rowwise(),colwise()は全ての行に対して、あるいは全ての列に対して処理をしたい時に使う演算子みたいなもの。

例えばmean()は平均を計算する関数なので、colwise().mean()で各列の平均値を求めることができる

Eigen::MatrixXf mat(2, 3);

mat.row(0) << 1, 3, 5;
mat.row(1) << 2, 4, 6;

std::cout << mat.colwise().mean() << std::endl;

結果：

1.5 3.5 5.5

つまり、各行の値に対して、これらを引けばよいので、

mat.rowwise().operator-()

を呼び出す。

標準偏差

標準偏差は、全ての列のデータに対して、平均値を引いてそれを二乗したものを合計するわけだが、その計算をcolwise()で（なぜか）行えないので、一度arrayに変換する必要がある。

auto col = mat.col(c).array();

arrayに変換したら、arrayの各要素に対して演算を行える関数が用意されているので、それを駆使して列ごとに標準偏差を求める。

double std_dev = sqrt(
  (col/*各要素から*/ - col.mean()/*全要素の平均を引き*/)
    .square()/*それぞれ二乗して*/
      .sum()/*全て合計して*/
        / col.size()/*要素数で割り*/
)/*平方根をとる*/;

各列の要素を、標準偏差で割る。

centered.col(c) /= std_dev;

分散共分散行列

さっぱりわからん

おまけ PCA

主成分分析はEigenSolverに上記で計算した分散共分散行列のcovを入れて行うらしい。

//Eigen::SelfAdjointEigenSolver<Eigen::MatrixXf> es(cov);
Eigen::EigenSolver<Eigen::MatrixXf> es(cov);
Eigen::MatrixXcf eigen_vectors = es.eigenvectors();
Eigen::VectorXcf eigen_values = es.eigenvalues();

最後に

そもそもcovは分散共分散行列というヤツなのか？私は主成分分析をするにはそれにする必要があるらしいので、それに用いることができるならそれであろうという認識であって数学的な事は何一つ理解していないのだが。

コメントを残すコメントをキャンセル

この記事のトラックバックURL：