スポンサーリンク
線分の交差判定するコード
線分の交差判定を行う。二次元画像の場合、結果がピクセル単位になるため座標の四捨五入が必要。
LineCross.hpp
#pragma once
template<typename ScalarT> struct Point { ScalarT x, y; Point(const ScalarT X, const ScalarT Y) :x(X), y(Y) {} template<typename T> Point(const Point<T>& src) { x = src.x; y = src.y; } Point() {} }; template<typename ScalarT> struct LineSegment { Point<ScalarT> s, e; template<typename T> LineSegment(const Point<T>& S, const Point<T>& E) :s(S), e(E) {} template<typename T> LineSegment(const LineSegment<T>& LS):s(LS.s),e(LS.e){} LineSegment() {} };
using Pointd = Point<double>; using LineSegmentd = LineSegment<double>;
//! @brief 線分の交点を求める //! @param [out] cross 交点座標の格納先 //! @param [in] L1 線分1 //! @param [in] L2 線分2 //! @retval true 交差している //! @retval false 交差していない bool isCross(Pointd* cross, const LineSegmentd& L1, const LineSegmentd& L2) { const double Ax = L1.s.x; const double Ay = L1.s.y; const double Bx = L1.e.x; const double By = L1.e.y; const double Cx = L2.s.x; const double Cy = L2.s.y; const double Dx = L2.e.x; const double Dy = L2.e.y; //分子 const double s_numerator = (Cx - Ax)*(Dy - Cy) - (Cy - Ay)*(Dx - Cx); //分母 const double s_denominator = (Bx - Ax)*(Dy - Cy) - (By - Ay)*(Dx - Cx); //分子 const double t_numerator = (Ax - Cx)*(By - Ay) - (Ay - Cy)*(Bx - Ax); //分母 const double t_denominator = (Dx - Cx)*(By - Ay) - (Dy - Cy)*(Bx - Ax); const double s = s_numerator / s_denominator; const double t = t_numerator / t_denominator; if ( 0 <= s && s <= 1 && 0 <= t && t <= 1 ) { cross->x = Ax + s * (Bx - Ax); cross->y = Ay + s * (By - Ay); return true; } return false; }
using Pointi = Point<int>; using LineSegmenti = LineSegment<int>;
//! @brief ピクセル単位を想定して線分の交差判定を行う bool isCrossPixel(Pointi* P, const LineSegmenti a, const LineSegmenti b) { LineSegmentd da(a); LineSegmentd db(b); Pointd c; if (isCross(&c, da, db) == false) return false; P->x = (int)round(c.x);// 四捨五入 P->y = (int)round(c.y);// 四捨五入 return true; }
テストコード
以前書いたBresenhamとデータ用にNByteDataを使用している。
#pragma warning(disable:4996) #include <iostream> #include <vector> #include <random> // 乱数用 #include "Bresenham.hpp" #include "NByteData.hpp" #include "LineCross.hpp" void ppmP3_write( const char* const fname, const int width, const int height, const unsigned char* const p, const int vmax );
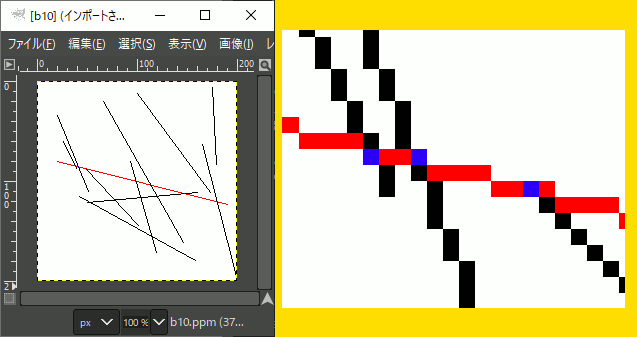
int main() { using ucrgb = NByteData<3>; int width = 200; int height = 200; std::vector<ucrgb> image; ucrgb Black = ucrgb{ 0,0,0 }; ucrgb White = ucrgb{ 255,255,255 }; ucrgb Red = ucrgb{ 255,0,0 }; ucrgb Blue = ucrgb{ 0,0,255 }; image.resize(width*height, White); // 疑似乱数 std::mt19937 mt(2); // 0~5の範囲の一様乱数作成用 // float型が欲しいなら std::uniform_real_distribution<> std::uniform_int_distribution<> idistriW(0, width-1); std::uniform_int_distribution<> idistriH(0, height-1); //赤い線分 const LineSegmenti A( Pointi(20,80),Pointi(190,123) ); Bresenham(image.data(), width, height, A.s.x, A.s.y, A.e.x, A.e.y, Red); for (size_t i = 0; i < 10; i++) { int x1 = idistriW(mt); int y1 = idistriH(mt); int x2 = idistriW(mt); int y2 = idistriH(mt); //黒い線分 LineSegmenti B(Pointi(x1,y1), Pointi(x2,y2) ); Bresenham(image.data(), width, height, B.s.x, B.s.y, B.e.x, B.e.y, Black); //交点があれば着色 Pointi c; if (isCrossPixel(&c, A, B) == true) { image[c.y*width + c.x] = Blue; } } //ファイル保存 char fname[100]; sprintf(fname, R"(C:\test\ret.ppm)", 10); ppmP3_write(fname, width, height, image.data()->data(), 255); }
//! @brief PPM(RGB各1byte,カラー,テキスト)を書き込む //! @param [in] fname ファイル名 //! @param [in] width 画像の幅 //! @param [in] height 画像の高さ //! @param [in] p 画像のメモリへのアドレス //! @param [in] vmax 全てのRGBの中の最大値。普通の画像なら255 //! @details RGBRGBRGB....のメモリを渡すと、RGBテキストでファイル名fnameで書き込む void ppmP3_write( const char* const fname, const int width, const int height, const unsigned char* const p, const int vmax ) { FILE* fp = fopen(fname, "wb"); fprintf(fp, "P3\n%d %d\n%d\n", width, height, vmax); size_t k = 0; for (size_t i = 0; i < (size_t)height; i++) { for (size_t j = 0; j < (size_t)width; j++) { fprintf(fp, "%d %d %d ", p[k * 3 + 0], p[k * 3 + 1], p[k * 3 + 2] ); k++; } fprintf(fp, "\n"); } fclose(fp); }
この記事のトラックバックURL: