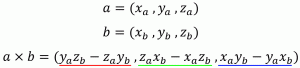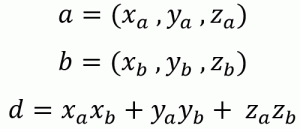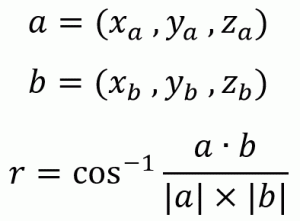C言語で、ある三次元ベクトルに垂直なベクトルを求める

//! @brief 三次元ベクトルの外積を求める
//! @param [out] dvec 求めたベクトル
//! @param [in] svec1 一つ目の三次元ベクトル
//! @param [in] svec2 二つ目の三次元ベクトル
//! @return なし
void outer(double * const dvec, double const * const svec1, double const * const svec2) {

  const double& xa = svec1[0];
  const double& ya = svec1[1];
  const double& za = svec1[2];
  const double& xb = svec2[0];
  const double& yb = svec2[1];
  const double& zb = svec2[2];

  dvec[0] = ya * zb - za * yb;
  dvec[1] = za * xb - xa * zb;
  dvec[2] = xa * yb - ya * xb;
}

//! @brief ベクトルの内積を求める
//! @param [in] vec1 一つ目の三次元ベクトル
//! @param [in] vec2 二つ目の三次元ベクトル
//! @return 内積
double inner(double const * const vec1, double const * const vec2) {
  const double& xa = vec1[0];
  const double& ya = vec1[1];
  const double& za = vec1[2];
  const double& xb = vec2[0];
  const double& yb = vec2[1];
  const double& zb = vec2[2];

  return (xa*xb + ya*yb + za*zb);
}

//! @brief ベクトルの長さを求める関数
//! @param [in] vec 三次元ベクトル
//! @return 長さ
double vlen(double const * const vec) {
  const double& x = vec[0];
  const double& y = vec[1];
  const double& z = vec[2];

  return sqrt(x * x + y * y + z * z);
}

//! @brief 二つのベクトルの角度をラジアンで求める関数
//! @param [in] vec1 一つ目の三次元ベクトル
//! @param [in] vec2 二つ目の三次元ベクトル
//! @return 二つのベクトルのなす角（ラジアン）
double vangle(double const * const vec1, double const * const vec2) {
  return acos(inner(vec1, vec2) / (vlen(vec1) * vlen(vec2)));
}

//! @brief ある三次元ベクトルに垂直な三次元ベクトルを求める
//! @param [out] dst3 結果の格納先
//! @param [in] src3 三次元ベクトル
void rightvec(double* dst3, double* src3) {

  double tmp[3] = { 1,0,0 };

  //tmpとsrc3の角度０またはそれに近いなら、別なベクトルを用意
  if (vangle(tmp, src3) < 0.00174533) { //0.00174533rad=1degree
    tmp[0] = 0;
    tmp[1] = 1;
    tmp[2] = 0;
  }
  //外積を求める
  outer(dst3, tmp, src3);
}

#include <Windows.h>
#include <gl/GL.h>
#include <gl/freeglut.h>
#include <math.h>
#pragma comment(lib,"opengl32.lib")
#pragma comment(lib,"freeglut.lib")

void display(void)
{
  glClear(GL_COLOR_BUFFER_BIT);

  glMatrixMode(GL_MODELVIEW);
  glLoadIdentity();

  glTranslated(0.0, 0.0, -5.0);

  glPushMatrix();
  static double deg = 0;
  deg = deg + 1;
  glRotated(deg, 0, 1, 0);

  glColor3d(1, 0, 0);
  //一本目のベクトルを表示
  double src3[3] = { 2,-3,4 };
  glBegin(GL_LINES);
  glVertex3d(0, 0, 0);
  glVertex3dv(src3);
  glEnd();

  glColor3d(0, 1, 0);
  double dst3[3];
  rightvec(dst3, src3);
  //二本目のベクトルを表示
  glBegin(GL_LINES);
  glVertex3d(0, 0, 0);
  glVertex3dv(dst3);
  glEnd();


  glPopMatrix();


  glFlush();
}
void timer(int value) {
  glutPostRedisplay();
  glutTimerFunc(50, timer, 0);
}
void init(void)
{
  glClearColor(0.0, 0.0, 1.0, 1.0);
}
void resize(int w, int h)
{
  glViewport(0, 0, w, h);

  glMatrixMode(GL_PROJECTION);
  glLoadIdentity();
  gluPerspective(30.0, (double)w / (double)h, 1.0, 100.0);
}
int main(int argc, char *argv[])
{
  glutInit(&argc, argv);
  glutInitDisplayMode(GLUT_RGBA);
  glutCreateWindow(argv[0]);
  glutDisplayFunc(display);
  glutReshapeFunc(resize);
  glutTimerFunc(100, timer, 0);
  init();
  glutMainLoop();
  return 0;
}