Welzlの最小球を求めるアルゴリズムをC++で実装

#include <iostream>
#include <unordered_map>
#include <set>

#pragma warning(disable:4996)

#include <vtkUnsignedCharArray.h>
#include <vtkPointData.h>
#include <vtkActor.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>

#include <vtkProperty.h>

#include <vtkSphere.h>

#include <vtkVertexGlyphFilter.h>

//球とその表示に必要
#include <vtkSphereSource.h>
#include <vtkPolyDataMapper.h>

//VTK_MODULE_INITに必要
#include <vtkAutoInit.h>

//必須
VTK_MODULE_INIT(vtkRenderingOpenGL2);
VTK_MODULE_INIT(vtkInteractionStyle);

#pragma comment(lib, "ws2_32.lib")
#pragma comment(lib, "Psapi.lib")
#pragma comment(lib, "Dbghelp.lib")


#include <Eigen/Dense>
#include <random>

#pragma comment(lib,"opengl32.lib")

// 点群型
struct MyCloud {
    std::vector<Eigen::Vector3d> points;
    std::vector<Eigen::Vector3d> colors;
};

namespace welzl {

    // 球を表す
    struct Sphere {
        Eigen::Vector3d center;
        double radius;
        Sphere() : center(Eigen::Vector3d::Zero()), radius(0.0) {}
        Sphere(const Eigen::Vector3d& c, double r) : center(c), radius(r) {}
    };
    

    //-------------------------------------
    // R（最大4点）から決まる球を求める補助関数群
    //-------------------------------------

    // 1点からなる球（その点が中心、半径0）
    Sphere ball_from_one_point(const Eigen::Vector3d& a) {
        return Sphere(a, 0.0);
    }
    

    // 2点からなる最小球（2点の中点が中心、半径は両点から中点までの距離）
    Sphere ball_from_two_points(const Eigen::Vector3d& a, const Eigen::Vector3d& b) {
        Eigen::Vector3d c = 0.5 * (a + b);
        double r = (a - c).norm();
        return Sphere(c, r);
    }
    

    // 3点から決まる球（3点が共通で外接する円＝2次元平面での外接円を3D空間で表現）
    // 外接円の中心は3点からなる三角形の外心
    Sphere ball_from_three_points(const Eigen::Vector3d& a, const Eigen::Vector3d& b, const Eigen::Vector3d& c) {
        // 2次元外心計算を3次元対応。3点は同一平面上にあるため、
        // 外心は、(b - a), (c - a)に直交する2本の垂直二等分線の交点。
        Eigen::Vector3d ab = b - a;
        Eigen::Vector3d ac = c - a;

        Eigen::Matrix3d M;
        M << ab.x(), ab.y(), ab.z(),
            ac.x(), ac.y(), ac.z(),
            ab.cross(ac).x(), ab.cross(ac).y(), ab.cross(ac).z();

        // 上記はそのままでは重複があり、もう少し安定的な方法を取る必要がある。
        // 簡易的には、外心は以下の方程式で求められる：
        // |x - a|^2 = |x - b|^2 = |x - c|^2 を解く。
        // この方程式は線形代数で解ける。
        // 以下では直接外心を求める一般的な手続きの1つを示す。

        // 行列方程式で外心を求めるための設定
        // (参考実装) 外心は幾何的には以下で求まる：
        // Let A, B, C be points. 外心Oは:
        // solve for O:
        // (O - A)・(B - A) = (|B-A|^2)/2
        // (O - A)・(C - A) = (|C-A|^2)/2
        // この2式からOが求まる。（O - A）を未知変数にした線形方程式となる

        Eigen::Matrix2d A_mat;
        A_mat << ab.dot(ab), ab.dot(ac),
            ab.dot(ac), ac.dot(ac);
        Eigen::Vector2d rhs;
        rhs << 0.5 * ab.dot(ab),
            0.5 * ac.dot(ac);

        // 解く
        Eigen::Vector2d uv = A_mat.colPivHouseholderQr().solve(rhs);
        Eigen::Vector3d O = a + uv[0] * ab + uv[1] * ac;

        double r = (O - a).norm();
        return Sphere(O, r);
    }
    

    // 4点から決まる球（4点が共通球面上にある場合、その外接球を求める）
    // 4点外接球計算は3x3の線形方程式を解くことで可能。
    Sphere ball_from_four_points(const Eigen::Vector3d& a, const Eigen::Vector3d& b,
        const Eigen::Vector3d& c, const Eigen::Vector3d& d) {
        // 方針：
        // (O - a)・(O - a) = (O - b)・(O - b)
        // (O - a)・(O - a) = (O - c)・(O - c)
        // (O - a)・(O - a) = (O - d)・(O - d)
        // という3つの方程式を立て、Oを求める。

        Eigen::Vector3d A = a;
        Eigen::Vector3d B = b;
        Eigen::Vector3d C = c;
        Eigen::Vector3d D = d;

        // 方程式組み立て
        // (O - A)² = (O - B)² などは展開すると
        // O² - 2O·A + A² = O² - 2O·B + B² → 2O·(B - A) = B² - A²
        // 同様にC, Dについても同様の式を立てられる
        // よって:
        // 2(B - A)·O = B² - A²
        // 2(C - A)·O = C² - A²
        // 2(D - A)·O = D² - A²

        // ベクトルX = Oについて
        Eigen::Matrix3d M;
        M << 2 * (b.x() - a.x()), 2 * (b.y() - a.y()), 2 * (b.z() - a.z()),
            2 * (c.x() - a.x()), 2 * (c.y() - a.y()), 2 * (c.z() - a.z()),
            2 * (d.x() - a.x()), 2 * (d.y() - a.y()), 2 * (d.z() - a.z());

        auto sq = [](const double& val) { return val * val; };

        Eigen::Vector3d RHS;
        RHS << (b.squaredNorm() - a.squaredNorm()),
            (c.squaredNorm() - a.squaredNorm()),
            (d.squaredNorm() - a.squaredNorm());

        Eigen::Vector3d O = M.colPivHouseholderQr().solve(RHS);

        double r = (O - a).norm();
        return Sphere(O, r);
    }
    

    // Rには最大４頂点が入っている。
    // それに応じて最小包含球を求める
    Sphere ball_from_R(const std::vector<Eigen::Vector3d>& R) {
        switch (R.size()) {
        case 0:
            return Sphere(Eigen::Vector3d::Zero(), 0.0);
        case 1:
            return ball_from_one_point(R[0]);
        case 2:
            return ball_from_two_points(R[0], R[1]);
        case 3:
            return ball_from_three_points(R[0], R[1], R[2]);
        case 4:
            return ball_from_four_points(R[0], R[1], R[2], R[3]);
        default:
            // それ以上はありえない
            return Sphere();
        }
    }
    

    //-------------------------------------
    // 点 p が球 S の中に入っているか判定
    //-------------------------------------

    inline bool is_in_sphere(const Eigen::Vector3d& p, const Sphere& S) {
        return (p - S.center).squaredNorm() <= S.radius * S.radius + 1e-14; // 浮動小数対策
    }

    //-------------------------------------
    // Welzlの再帰関数
    //-------------------------------------
    // 引数：
    // points: 対象の点集合（インデックス0〜endで使用）
    // R: 球を定義するための点集合
    // end: 再帰処理内での有効点数境界

    Sphere welzl(const std::vector<Eigen::Vector3d>& points, std::vector<Eigen::Vector3d> R, int end) {

        // 再帰の末端、これ以上頂点がないか、Rが4点になったら球を求める
        if (end < 0 || R.size() == 4) {
            return ball_from_R(R);
        }

        // 頂点を一つ取り出して、それ以外の点で再帰処理
        Eigen::Vector3d p = points[end];
        Sphere D = welzl(points, R, end - 1);

        // 今取り出した点が、それ以外の点で求めた球に入っている場合
        // 球を再計算する必要が無いので、そのまま返す
        if (is_in_sphere(p, D)) {
            return D;
        }

        // pがD内に収まらない場合
        R.push_back(p);
        return welzl(points, R, end - 1);
    }

    //-------------------------------------
    // 公開関数: 最小包含球を計算
    //-------------------------------------
    Sphere minimum_enclosing_sphere(const std::vector<Eigen::Vector3d>& points) {

        // 頂点をシャッフルすると期待線形時間になるが
        // 頂点順を変えたくないため今回は使用しない
        // なお引数pointsがconst参照のため、ここを有効にしてもエラーになる。
        // 有効化するときは引数のconstを外すか、コピーを作成すること。
#if 0
        // ポイントシャッフル推奨（期待線形時間のため）
        std::random_device rd;
        std::mt19937 g(rd());
        std::shuffle(points.begin(), points.end(), g);
#endif
        std::vector<Eigen::Vector3d> dumyR;
        return welzl(points, dumyR, (int)points.size() - 1);
    }
    

}

std::pair<Eigen::Vector3f,float> CalcBoundingSphere(MyCloud& cloud) {
    welzl::Sphere S = welzl::minimum_enclosing_sphere(cloud.points);
    return { S.center.cast<float>(), S.radius };

}

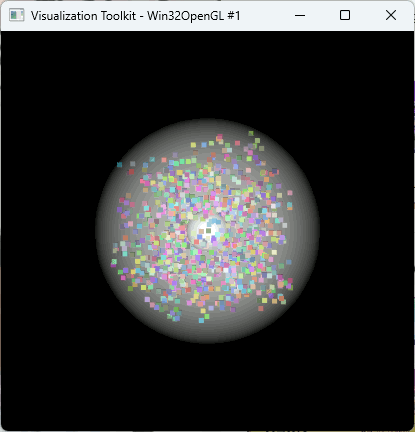
// 点群をVTK用のActorに変換
vtkSmartPointer<vtkActor> ConvertCloudVTKActor(const MyCloud& cloud);

// 座標と半径から球のActorを作成
vtkSmartPointer<vtkActor> CreateSphereActor(const std::pair<Eigen::Vector3f, float>& sphere_data);

// ランダムな点群を作成
MyCloud CreateRandomCloud(int num_points);



// 表示データを作成
bool PrepareData(vtkSmartPointer<vtkRenderer> renderer) {

    // ランダムな点群を作成
    auto cloud = CreateRandomCloud(1000);

    // welzlでBounding Sphereを計算
    auto sphere = CalcBoundingSphere(cloud);
    std::cout << "center : " << sphere.first.transpose() << std::endl;
    std::cout << "radius : " << sphere.second << std::endl;

    // VTK Actorを作成
    auto cloudActor = ConvertCloudVTKActor(cloud);
    auto sphereActor = CreateSphereActor(sphere);
    
    // Create a vtkSphereSource
    vtkSmartPointer<vtkSphereSource> sphereSource = vtkSmartPointer<vtkSphereSource>::New();
    sphereSource->SetCenter(sphere.first.x(), sphere.first.y(), sphere.first.z());
    sphereSource->SetRadius(0.3);
    sphereSource->SetThetaResolution(32);
    sphereSource->SetPhiResolution(32);

    // Create a vtkPolyDataMapper
    vtkSmartPointer<vtkPolyDataMapper> mapper = vtkSmartPointer<vtkPolyDataMapper>::New();
    mapper->SetInputConnection(sphereSource->GetOutputPort());

    // Create a vtkActor and assign the mapper
    vtkSmartPointer<vtkActor> CenterActor = vtkSmartPointer<vtkActor>::New();
    CenterActor->SetMapper(mapper);


    renderer->AddActor(cloudActor);
    renderer->AddActor(sphereActor);
    renderer->AddActor(CenterActor);
    return true;

}


// 座標と半径から球のActorを作成
vtkSmartPointer<vtkActor> CreateSphereActor(const std::pair<Eigen::Vector3f, float>& sphere_data) {
    // 球の中心と半径を取得
    const Eigen::Vector3f& center = sphere_data.first;
    float radius = sphere_data.second;

    // vtkSphereSourceを設定
    vtkSmartPointer<vtkSphereSource> sphereSource = vtkSmartPointer<vtkSphereSource>::New();
    sphereSource->SetCenter(center.x(), center.y(), center.z());
    sphereSource->SetRadius(radius);
    sphereSource->SetThetaResolution(32); // 解像度設定
    sphereSource->SetPhiResolution(32);  // 解像度設定

    // Mapperを作成
    vtkSmartPointer<vtkPolyDataMapper> mapper = vtkSmartPointer<vtkPolyDataMapper>::New();
    mapper->SetInputConnection(sphereSource->GetOutputPort());

    // Actorを作成
    vtkSmartPointer<vtkActor> actor = vtkSmartPointer<vtkActor>::New();
    actor->SetMapper(mapper);

    // 半透明に設定
    actor->GetProperty()->SetOpacity(0.5); // 透明度（0.0～1.0）
    actor->GetProperty()->SetColor(1.0, 1.0, 1.0); // 白

    return actor;
}

// ランダムな点群を作成
MyCloud CreateRandomCloud(int num_points) {
    MyCloud cloud;
    std::random_device seed_gen;
    std::mt19937 engine(seed_gen());
    std::uniform_real_distribution<> dist(-1.0, 1.0);

    for (int i = 0; i < num_points; i++) {
        cloud.points.emplace_back(dist(engine), dist(engine), dist(engine));
        cloud.colors.emplace_back(dist(engine), dist(engine), dist(engine));
    }

    return cloud;
}

// 点群をVTK用のActorに変換
vtkSmartPointer<vtkActor> ConvertCloudVTKActor(const MyCloud& cloud) {
    // VTK用のポイントリストを作成
    auto points = vtkSmartPointer<vtkPoints>::New();
    for (const auto& point : cloud.points) {
        points->InsertNextPoint(point.x(), point.y(), point.z());
    }

    // VTK用の頂点色リストを作成（Open3Dのcolors_を使用）
    auto colors = vtkSmartPointer<vtkUnsignedCharArray>::New();
    colors->SetNumberOfComponents(3); // RGB
    if (!cloud.colors.empty()) {
        for (const auto& color : cloud.colors) {
            unsigned char r = static_cast<unsigned char>(color.x() * 255);
            unsigned char g = static_cast<unsigned char>(color.y() * 255);
            unsigned char b = static_cast<unsigned char>(color.z() * 255);
            colors->InsertNextTuple3(r, g, b);
        }
    }

    // ポリデータに点とオプションの属性（色、法線）を設定
    auto polyData = vtkSmartPointer<vtkPolyData>::New();
    polyData->SetPoints(points);
    if (!cloud.colors.empty()) {
        polyData->GetPointData()->SetScalars(colors);
    }

    // 点を頂点として描画可能にするフィルター
    auto glyphFilter = vtkSmartPointer<vtkVertexGlyphFilter>::New();
    glyphFilter->SetInputData(polyData);
    glyphFilter->Update();

    // マッパーを作成
    auto mapper = vtkSmartPointer<vtkPolyDataMapper>::New();
    mapper->SetInputData(glyphFilter->GetOutput());
    if (!cloud.colors.empty()) {
        mapper->ScalarVisibilityOn(); // 頂点色を使用する
    }
    else {
        mapper->ScalarVisibilityOff(); // 頂点色がない場合はオフ
    }


    // Actorを作成
    auto actor = vtkSmartPointer<vtkActor>::New();
    actor->SetMapper(mapper);
    actor->GetProperty()->SetPointSize(5.0);

    actor->GetProperty()->SetInterpolationToFlat();

    return actor;
}



int main()
{

    vtkSmartPointer<vtkRenderer> renderer = vtkSmartPointer<vtkRenderer>::New();

    vtkSmartPointer<vtkRenderWindow> window = vtkSmartPointer<vtkRenderWindow>::New();
    window->AddRenderer(renderer);


    vtkSmartPointer<vtkRenderWindowInteractor> interactor = vtkSmartPointer<vtkRenderWindowInteractor>::New();
    window->SetInteractor(interactor);

    PrepareData(renderer);

    window->SetSize(700, 400);

    interactor->Initialize();

    window->Render();
    interactor->Start();

}